公钥密码体制

公钥密码体制的基本概念；RSA公钥加密原理；ElGamal公钥加密原理；椭圆曲线密码系统；SM2算法。

基本概念

公钥密码采用两个密钥将加密和解密能力分开，通信双方无需事先交换密钥就可通信，并且已知公钥和密文的情况下获取密文或私钥在计算上不可行。由于公钥体制加密变换公开，任何人均可进行选择明文攻击，因此明文空间必须足够大防止穷举明文空间攻击。
单向函数：任何条件下求逆都困难的函数。
陷门单向函数：在不知道陷门消息的情况下求逆困难的函数。陷门可能不止一个，若陷门信息保密性不强，也会容易求逆。
公钥系统：在一个公钥系统中，所有用户共同选定一个陷门单向函数、加密运算E、可用消息集鉴别函数F。用户i从陷门集中选定zi，并公开可用消息集Fzi、Ezi，任意用户想要发送消息x给用户i，先使用Fzi验证x是否在消息可用集中，然后y = Ezi(x)发送给用户i。任一用户仅通过y，Fzi，Ezi无法得到x，但用户i在已知zi的情况下容易得到x = Dzi(y)。
用于构造公钥密码的单向函数：

• 多项式求根：在有限域GF(p )上已知系数、x、p求y容易，已知y、系数、p求解x困难。

• 大整数分解

• 离散对数问题DL
  

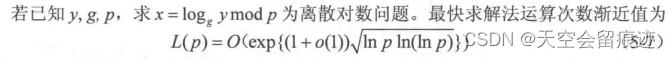
• DHP

RSA加密原理

利用大整数分解。选取两个大素数q1，q2，n=q1×q2，$\Phi (n)=(q_1-1)(q_2-1)$，随机选取整数e，$1\le e<\Phi (n)$ 且 $gcd(e,\Phi (n))=1$，则在模$\Phi (n)$下e有逆元，$d=e^{-1}mod\Phi (n)$。
公钥：n，e
私钥：d
加密：将明文分组，各组在modn的情况下可以唯一地表示出来。可用明文集 A z i = { x ∣ 1 ≤ x < n , ( x , n ) = 1 } A_{zi} = \left\{x|1 \leq x<n,(x,n)=1 \right\} Azi​={x∣1≤x<n,(x,n)=1},$y=x^{e}modn$
解密：$x=y^{d}modn$

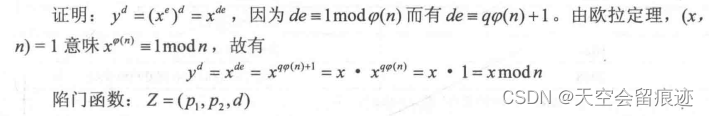
ElGamal加密原理

利用离散对数问题。Zp是有p个元素有限域，p是素数，g是Zp*生成元。
公钥：选定g计算公钥$\beta =g^{\alpha }modp$
公钥加密：选择随机数k，$y_1=g^{k}modp$ ,$y_2=m{\beta }^{k}modp$，发送y1||y2
私钥解密：$m=y_2/y_1^{\alpha }$
特点：由于随机数k的存在，对同一消息在不同时刻加密结果不同。但由于密文级联而成，密文消息长扩展为原来两倍。

椭圆曲线密码系统

使用到的椭圆曲线的特性：
对称性：椭圆曲线$y^2=x^3+ax+b$关于y轴对称。
单位元：如果椭圆曲线上三点共线，那么它们的和为O，O是椭圆曲线加法单位元，O=-O。对于椭圆曲线上任意一点P,有P+O=P，P的加法逆元为P’=-P=(x,-y)，因为做过P、-P的直线，在无穷远处得到椭圆曲线上的点O，有P+P’+O=O，即P=-P。
椭圆曲线加法：Q，R两点连线延长与椭圆曲线交于P，则Q+R+P=O,即Q+R=-P。
点Q的倍数：过点Q做椭圆曲线切线，设与椭圆曲线相交于S，定义2Q=Q+Q=-S。

椭圆曲线加密
将要发送的消息明文编码成椭圆曲线上的点$P_m=(x,y)$；挑选大整数q,选择椭圆曲线参数，定义椭圆群$E_q(a,b)$，在$E_q(a,b)$中挑选基点$G(x_1,y_1)$,G的阶为非常大的整数n(nG = O)。每个用户选定私钥。
用户B选定$n_B$,则公钥$P_B=n_{B}G$
用户A向用户B传递消息$P_m$：$c=(kG,P_m+k{P}_B)$
用户B解密：$P_m=(P_m+k{P}_B)-n_B(kG)$
椭圆曲线密码安全性：基于椭圆曲线的离散对随难题：给定P和 kP 计算k非常困难。与具有同等安全性的RSA相比，椭圆曲线使用更短的密钥。

SM2算法

SM2椭圆曲线需要运用的辅助函数有：SM3杂凑函数$H_v$输出长为v的杂凑值、密钥派生函数KDF(用到SM3)、随机数发生器。
参数：有限域$F_q$规模q，定义椭圆曲线$E(F_q)$两个元素a,b; 椭圆曲线的基点G; G的阶n以及其他可选项，如n 的余因子h。用户选定私钥d∈{1,…,n-1}，公钥：P=dG
加密关键过程
用户A向用户B传输：明文M，长klen
输出密文：$C=C_1||C_2||C_3$，
用户A已知公钥$P_B$，使用随机数发生器产生随机数k∈{1,…,n-1}
C1: $C_1=kG=(x_1,y_1)$
C3: 计算椭圆曲线上点$S=h{P}_B$若S是无穷远点就报错退出，计算$k{P}_B=(x_2,y_2)$，则$C_3=Hash(x_2||M||y_2)$
C2: $C_2=M\oplus t$，$t=KDF(x_2||y_2,klen)$，其中KDF(Z,klen),Z为输入的比特串，klen为输出长度。

//KDF伪代码
ct=0x00000001//初始化计数器
for(i=1,i<=ceil(klen/v);i++){
Hai = Hv(Z||ct);
ct++;
若klen/v非整数，最后一组只取最左侧的比特凑成总长为klen的输出
}
K=Ha1||Ha2||...||Hai //输出密钥数据比特串长度klen

算法加密流程图：

解密关键过程：$d_B{C}_1=(x_2,y_2)$，根据密文中C2长度得到klen，$t=KDF(x_2||y_2,klen)$。从$C$中取出$C_2$,计算$M^{\prime }=C_2\oplus t$；计算$u=Hash(x_2||M^{\prime }||y_2)$，若$u=C_3$输出M’，否则报错。
具体流程图：