本篇文章是博主在最化优学习、人工智能等领域学习时,用于个人学习、研究或者欣赏使用,并基于博主对相关等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在最优化算法:
最优化算法(5)---《基于粒子群算法(PSO)的TSP(Python实现)》
基于粒子群算法(PSO)的TSP(Python实现)
目录
1.项目介绍
基于粒子群算法(Particle Swarm Optimization, PSO)的TSP(Traveling Salesman Problem,旅行商问题),求解方法源自对集体智慧的模拟,通过模拟鸟群在搜索食物时的协作行为,不断调整每个“粒子”的位置和速度,以寻找全局最优解。在TSP问题中,粒子代表可能的路径解,通过不断更新粒子的位置,寻找一条最短的路径来访问所有城市。
PSO算法介绍:
PSO算法的核心思想是模拟鸟群的搜索行为,每个粒子代表一个潜在的解,在搜索空间中移动,并与其他粒子共同寻找最优解。在搜索过程中,粒子会记忆历史搜索中的最佳位置,并根据全局最优和局部最优位置进行位置的调整,从而促进了全局搜索和局部优化之间的平衡。这种协作机制使得PSO算法在处理TSP等组合优化问题时具有很好的全局搜索能力和收敛性。
实现PSO算法求解TSP问题的Python代码通常包括粒子位置更新、适应度评估、全局最优和局部最优更新等关键步骤。Python作为一种简洁而强大的编程语言,提供了丰富的科学计算库和可视化工具,非常适合实现PSO算法。通过合理的数据结构设计和算法实现,可以很好地完成TSP问题的求解,并将结果直观地展示出来。
值得注意的是,PSO算法中的参数设置对算法的性能影响较大,如惯性权重、加速系数等参数需要合理设置以平衡全局探索和局部开发。此外,PSO算法也面临着早熟收敛和参数选择的问题,在实际使用中需要谨慎调整参数以获得更好的结果。
算法的核心思想包括以下几个方面:
- 粒子位置更新:每个粒子代表一个潜在的解,其位置表示TSP路径上城市的访问顺序,根据当前速度和位置信息更新粒子的位置
- 全局最优和局部最优:粒子会记忆历史搜索中的最佳位置,同时借鉴全局最优位置,这种协作机制促进了全局搜索和局部优化之间的平衡
- 适应度评估:根据TSP路径长度等指标计算每个粒子的适应度,并据此更新全局最优和局部最优解
- 参数设置:PSO算法中需要合理设置惯性权重、加速系数等参数来平衡全局探索和局部开发
PSO算法求解TSP的基本思路包括:
- 初始化:初始化粒子群的位置和速度,记录全局最优和局部最优
- 粒子位置更新:根据速度和位置信息更新粒子的位置
- 适应度评估:计算每个粒子的适应度,并更新全局最优和局部最优解
- 最优路径更新:记录全局最优路径
- 终止条件:达到预设的迭代次数或满足特定条件时结束搜索,返回最优路径
通过利用PSO算法求解TSP问题,可以有效地寻找到较为优秀的旅行路线,尽管无法保证找到全局最优解,但通常能获得接近最优解的结果。粒子群算法在处理TSP等组合优化问题上具有很好的全局搜索能力和快速收敛性。
2.程序代码
""""
题目:基于粒子群算法的TSP
姓名:Rainbook
最终修改时间:2024.1.15
"""
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import time
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] # 使用微软雅黑字体
plt.rcParams['axes.unicode_minus'] = False # 处理负号显示异常
# 计算距离矩阵
def clac_distance(X, Y):
"""
计算两个城市之间的欧氏距离,二范数
:param X: 城市X的坐标.np.array数组
:param Y: 城市Y的坐标.np.array数组
:return:
"""
distance_matrix = np.zeros((city_num, city_num))
for i in range(city_num):
for j in range(city_num):
if i == j:
continue
distance = np.sqrt((X[i] - X[j]) ** 2 + (Y[i] - Y[j]) ** 2)
distance_matrix[i][j] = distance
return distance_matrix
# 定义总距离(路程即适应度值)
def fitness_func(distance_matrix, x_i):
"""
适应度函数
:param distance_matrix: 城市距离矩阵
:param x_i: PSO的一个解(路径序列)
:return:
"""
total_distance = 0
for i in range(1, city_num):
start_city = x_i[i - 1]
end_city = x_i[i]
total_distance += distance_matrix[start_city][end_city]
total_distance += distance_matrix[x_i[-1]][x_i[0]] # 从最后的城市返回出发的城市
return total_distance
# 定义速度更新函数
def get_ss(x_best, x_i, r):
"""
计算交换序列,即x2结果交换序列ss得到x1,对应PSO速度更新公式中的 r1(pbest-xi) 和 r2(gbest-xi)
:param x_best: pbest or gbest
:param x_i: 粒子当前的解
:param r: 随机因子
:return:
"""
velocity_ss = []
for i in range(len(x_i)):
if x_i[i] != x_best[i]:
j = np.where(x_i == x_best[i])[0][0]
so = (i, j, r) # 得到交换子
velocity_ss.append(so)
x_i[i], x_i[j] = x_i[j], x_i[i] # 执行交换操作
return velocity_ss
# 定义位置更新函数
def do_ss(x_i, ss):
"""
执行交换操作
:param x_i:
:param ss: 由交换子组成的交换序列
:return:
"""
for i, j, r in ss:
rand = np.random.random()
if rand <= r:
x_i[i], x_i[j] = x_i[j], x_i[i]
return x_i
def draw(best):
result_x = [0 for col in range(city_num + 1)]
result_y = [0 for col in range(city_num + 1)]
for i in range(city_num):
result_x[i] = city_x[best[i]]
result_y[i] = city_y[best[i]]
result_x[city_num] = result_x[0]
result_y[city_num] = result_y[0]
plt.xlim(0, 5) # 限定横轴的范围
plt.ylim(0, 4) # 限定纵轴的范围
plt.plot(result_x, result_y, marker='>', mec='r', mfc='w', label=u'路线')
plt.legend() # 让图例生效
plt.margins(0)
plt.subplots_adjust(bottom=0.15)
for i in range(len(best)):
plt.text(result_x[i] + 0.05, result_y[i] + 0.05, str(best[i] + 1), color='red')
plt.xlabel('横坐标')
plt.ylabel('纵坐标')
plt.title('轨迹图')
plt.show()
def print_route(route):
result_cur_best = []
for i in route:
result_cur_best += [i]
for i in range(len(result_cur_best)):
result_cur_best[i] += 1
result_path = result_cur_best
result_path.append(result_path[0])
return result_path
if __name__ == "__main__":
# 参数定义
CityCount = 30 # 定义城市个数
# uniform()生成10个二维数组,数值范围是0到2000
city_x = np.random.uniform(0, 2000, (1, CityCount))
city_x = city_x[0, :].tolist()
city_y = np.random.uniform(0, 2000, (1, CityCount))
city_y = city_y[0, :].tolist()
city_num = CityCount
size = 500 # 粒子数量
r1 = 0.7 # 个体学习因子
r2 = 0.8 # 社会学习因子
iter_max_num = 500 # 迭代次数
fitness_value_lst = []
distance_matrix = clac_distance(city_x, city_y)
# 初始化种群各个粒子的位置,作为个体的历史最优pbest
pbest_init = np.zeros((size, city_num), dtype=np.int64)
for i in range(size):
pbest_init[i] = np.random.choice(list(range(city_num)), size=city_num, replace=False)
# 计算每个粒子对应的适应度
pbest = pbest_init
pbest_fitness = np.zeros((size, 1))
for i in range(size):
pbest_fitness[i] = fitness_func(distance_matrix, x_i=pbest_init[i])
# 计算全局适应度和对应的gbest
gbest = pbest_init[pbest_fitness.argmin()]
gbest_fitness = pbest_fitness.min()
# 记录算法迭代效果
fitness_value_lst.append(gbest_fitness)
# 迭代过程
for i in range(iter_max_num):
# 控制迭代次数
for j in range(size):
# 遍历每个粒子
pbest_i = pbest[j].copy()
x_i = pbest_init[j].copy()
# 计算交换序列,即 v = r1(pbest-xi) + r2(gbest-xi)
ss1 = get_ss(pbest_i, x_i, r1)
ss2 = get_ss(gbest, x_i, r2)
ss = ss1 + ss2
x_i = do_ss(x_i, ss)
fitness_new = fitness_func(distance_matrix, x_i)
fitness_old = pbest_fitness[j]
if fitness_new < fitness_old:
pbest_fitness[j] = fitness_new
pbest[j] = x_i
gbest_fitness_new = pbest_fitness.min()
gbest_new = pbest[pbest_fitness.argmin()]
if gbest_fitness_new < gbest_fitness:
gbest_fitness = gbest_fitness_new
gbest = gbest_new
fitness_value_lst.append(gbest_fitness)
print("第%d迭代,最优值为:%s" % (i, gbest_fitness))
# 输出迭代结果
print("===最优路线:", print_route(gbest))
print("===最优值:", gbest_fitness)
# 绘图
# 迭代完成后最优路线的示意图
X = city_x
Y = city_y
x = []
y = []
for city in gbest:
x.append(X[city])
y.append(Y[city])
x.append(X[gbest[0]])
y.append(Y[gbest[0]])
plt.figure(1)
for j in range(len(gbest)):
plt.quiver(x[j], y[j], x[j + 1] - x[j], y[j + 1] - y[j], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x[-1], y[-1], x[0] - x[-1], y[0] - y[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
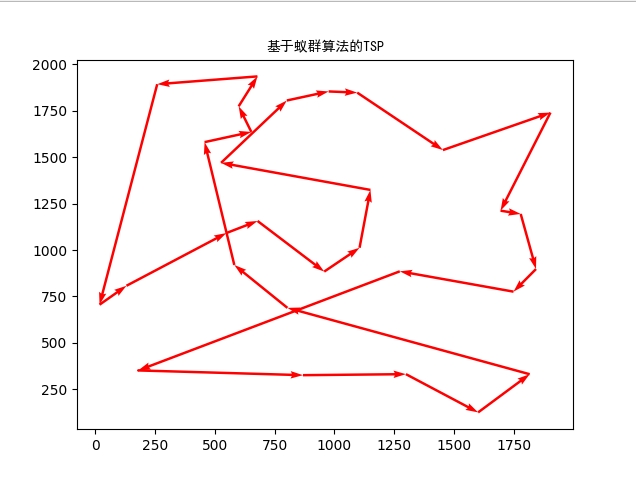
plt.title("基于蚁群算法的TSP")
plt.figure(2)
plt.plot(fitness_value_lst)
plt.title('优化过程')
plt.ylabel('最优值')
plt.xlabel('迭代次数')
plt.show()
3.运行结果
参考资料来源:CSDN、百度搜索、维基百科等
文章若有不当和不正确之处,还望理解与指出。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请联系博主删除。如有错误、疑问和侵权,欢迎评论留言联系作者,或者关注VX公众号:Rain21321,联系作者。




























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










