现代谱估计分析信号的功率谱（1）---AR 模型谱估计

不去幼儿园

于 2024-06-19 16:43:13 发布

阅读量3.4k

点赞数 32

分类专栏： # 通讯领域笔记经验分享文章标签： AR模型谱估计信号处理功率谱

本文链接：https://blog.csdn.net/qq_51399582/article/details/139805799

版权

经验分享同时被 2 个专栏收录

28 篇文章

订阅专栏

通讯领域笔记

11 篇文章

订阅专栏

本篇文章是博主在通信等领域学习时，用于个人学习、研究或者欣赏使用，并基于博主对通信等领域的一些理解而记录的学习摘录和笔记，若有不当和侵权之处，指出后将会立即改正，还望谅解。文章分类在通信领域笔记：

通信领域笔记（5）---《现代谱估计分析信号的功率谱（1）---AR 模型谱估计》

现代谱估计分析信号的功率谱（1）---AR 模型谱估计

1 背景分析

现代谱估计是一种用于分析信号的功率谱的技术。与传统的基于傅里叶变换的经典谱估计方法相比，现代谱估计具有更高的分辨率和更准确的频率估计能力。传统谱估计方法主要基于傅里叶变换，将信号从时域转换到频域，然后计算各个频率成分的功率。但是，傅里叶变换对于非周期信号和有限长度的信号存在分辨率限制，即无法准确区分频率相近的成分。此外，傅里叶变换还受到窗函数选择和泄漏效应的影响，可能导致谱估计的偏差。

现代谱估计方法通过利用信号的自相关函数或协方差函数等统计特性，以及先进的数学工具和算法，提高了谱估计的分辨率和准确性。其中一些常见的方法包括自回归模型（AR模型）、最大熵谱估计（MESP）、最小方差无偏估计（MVUE）等。这些方法利用了信号中的统计信息，可以更好地分辨频率相近的成分，并减小窗函数选择和泄漏效应的影响。

现代谱估计方法的发展受益于信号处理、统计学和计算机科学等多个领域的进步。随着技术的不断发展，现代谱估计方法将在更多领域得到应用，并为信号处理和数据分析提供更准确、更有效的工具。

本次实验主要验证在时间序列分析中，AR 模型（自回归模型）和皮萨伦科（Pisarenko）分析方法的相关问题。

皮萨伦科（Pisarenko）分析方法见通信领域笔记专栏：

《现代谱估计分析信号的功率谱（2）---Pisarenko 谐波分解法》

1.1 设计要求

通过 MATLAB 软件产生如下信号：

𝑥(𝑛) = 2 cos(2𝜋𝑓1𝑛) + 2 cos(2𝜋𝑓2𝑛) 2 cos(2𝜋𝑓3𝑛) + 𝑣(𝑛)

其中𝑓1 = 0.05、𝑓2 = 0.40、𝑓3 = 0.42，𝑣(𝑛)是实高斯白噪声（信噪比由 5dB 至-10dB，步进 5dB），𝑓1-𝑓3均为归一化的频率。

1）使用 AR 模型对信号进行功率谱估计，模型参数计算分别使用自相关法，协方差法。而后与经典谱估计进行对比分析，并且验证模型阶数变化时带来的影响。

2）使用皮萨伦科（Pisarenko）分析信号成分。

2 理论分析推导

信号建模谱估计是现代谱估计的重要方法，其中 AR 模型功率谱估计是最常用的一种方法，这是因为 AR 模型参数的精确估计可以用解一组线性方程的方法求得，而对于 MA 或 ARMA 模型功率谱估计来说，其参数的精确估计需要解一组高阶的非线性方程。所以实验的现代谱估计内容以 AR 模型谱估计为主来进行实验分析和验证。

2.1 AR 模型谱估计原理

2.2 AR 模型谱估计步骤

3 MATLAB 仿真

3.1 AR 模型谱估计

首先采用归一化载波频率，设置采样点数为，生成三个不同频率的余弦信号，最后使用 awgn 函数加入高斯白噪声，生成信号𝑥𝑛。

N=200;%采样点数
Fs = 1000;  %采样频率
fc1 = 0.05*Fs; % 归一化载波频率转化为载波频率
fc2 = 0.40*Fs;
fc3 = 0.42*Fs;
n = 0:1/Fs:(N-1)/Fs;

xn = 2*cos(2*pi*fc1*n) + 2*cos(2*pi*fc2*n) + 2*cos(2*pi*fc3*n);
xn = awgn(xn,5);  %加入高斯白噪声信号
nfft = N;
p=30;   %AR模型阶数
q=30;   %MA模型参数

3.1.1 AR 模型自相关法功率谱估计

直接调用 Matlab 中的 pyulear 函数估计功率谱，设置高斯白噪声信噪比 SNR 为 5。

%%自相关法求AR模型参数
[Pxx1,F1]=pyulear(xn,p,N,Fs);%直接调用matlab中的pyulear函数估计功率谱
Pxx1=10*log10(Pxx1);
figure(1);
plot(F1,Pxx1);
title('AR模型自相关法');

分别观察在不同的阶下，自相关法求解 AR 模型功率谱参数，阶次的选取以步进 8、10、20、30 为选择，分别得到了 AR 模型在 2 阶、10 阶、20 阶、30 阶、60 阶、80 阶、110 阶、130 阶的情况下得到的功率谱参数情况。

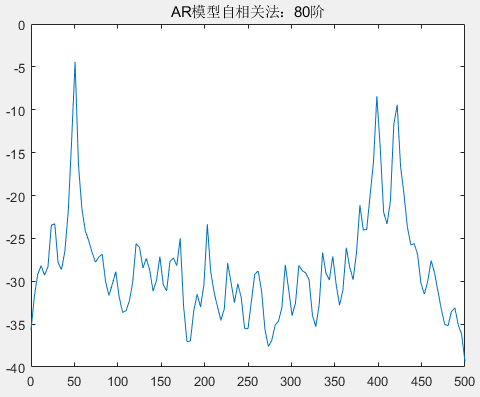
从图中可以看到，在阶次不断增加的情况下，归一化频率 0.4、0.42 的区分度由不清晰到区分度越来越清晰，但随着阶次的增高，尤其是在 80 阶以后，尽管分辨率比较高，但出现的虚假谱峰也越来越多。我们知道，一个经验法则是：AR 模型阶次应该选择在 𝑁/3 和𝑁/2之间，N 表示采样点数，这样可以得到谱估计的高分辨率。本次实验使用自相关法求谱估计参数时，选取的采样点数为 256，因此模型阶次的建议选择为 85<N<128，但根据目前的具体实验结果来看，选择30 阶的 AR 模型既可以区分 0.4、0.42 频率，也没有较多的虚假谱峰，因此优先选择 30 阶的 AR 模型进行谱估计。下面将采用协方差法求解不同次阶的 AR 模型，并分析。

3.1.2 AR 模型协方差法功率谱估计

直接调用 Matlab 中的 pburg 函数估计功率谱，设置高斯白噪声信噪比 SNR 为 5。

%%协方差法求AR模型参数
[Pxx2,F2]=pburg(xn,p,N,Fs);%直接调用matlab中的pburg估计功率谱
Pxx2=10*log10(Pxx2);
figure(2);
plot(F2,Pxx2);
title('AR模型协方差法');

从图中可以看到，在阶次低于 30 阶的情况下，归一化频率 0.4、0.42 的区分度由不清晰到区分度越来越清晰；但随着阶次的增高，在阶次 40 至 60 阶的情况下，出现了较大的虚假谱峰，导致无法区分归一化频率 0.4、0.42；尤其是在 60 阶以后，已经区分不了归一化频率 0.4、0.42。根据目前的具体实验结果来看，不论是自相关法还是协方差法的 AR 模型估计功率谱，选择 30 阶的 AR 模型既可以区分 0.4、0.42 频率，也没有较多的虚假谱峰，因此优先选择 30 阶的 AR 模型进行谱估计。下面将采用 30 阶的 AR 模型谱估计对比经典谱估计，并分析。

3.1.3 AR 模型与经典谱估计对比

采用经典谱估计的直接法和间接法估计功率谱，并对比 30 阶的 AR 模型自相关法和协方差法估计功率谱，初始信噪比 SNR 设置为 5dB，信噪比 SNR 步进幅度为-5dB。

由图可以看出，四种不同的谱估计方法在SNB=-5dB皆可以有效的估计出功率谱，能够清晰的区分相近频率。那么接下来将不断减小信噪比 SNR，比较功率谱估计情况。

还可以比较：

四种方法在 SNB=0dB 时功率谱估计都可以取得相对不错的效果。

四种方法在 SNB=-5dB 时功率谱估计都还可以区分相近频率点，但是经典谱估计的直接法出现的虚假谱峰较高，已经影响了判别。

四种方法在 SNB=-10dB 时，经典谱估计直接法已经无法识别，经典谱估计间接法功率、AR 模型谱估计自相关法和协方差法还勉强可以识别，经典谱估计间接法功率相对更优。

四种方法在 SNB=-15dB 时，此时四种方法皆不可以识别相近谱峰，无法使用这四种方法进行谱估计。