目录
10.快速排序2(Quicksort:PartitionRundom)
零.前言
分而治之的算法,即层层深入逐个突破,最终解决问题,就像玄幻小说斗破某穹里的主角一样,不可能上来就把魂族给灭了,得一步一步来,先灭个小家族,灭个佣兵团,再灭个什么门,灭个云岚宗,然后开始灭帝国,灭四方阁,灭魂殿,最后才轮到魂族。但是这些过程都惊人的相似,无非都是主角刚开始被揍的很惨(但总能带走一个),最后不断晋级将各个阶级团灭。这里就用到了分而治之的方法,虽然是一点一点从基层来解决问题,但是手段都是一样的,没有一个佛怒火莲解决不了的问题。。。
1.分治法
1.含义
将一个大的问题分解成若干个小的问题,并且这些小问题与大问题的问题性质保持一致,通过处理小问题从而处理大问题。这里用到了递归的思想。
2.分治法主要思想
1.分:将整个问题分成多个子问题。
2.求解:求解各个子问题。
3.合并:合并所有子问题的解,从而得到原始问题的解。
3.分治法的求解步骤
1.确定初始条件
设输入数据大小为n,T(n)为时间复杂度,且当n<c的时候,T(n)=θ(1)。这里是规定了下限,避免无限递归下去。这些内容不是自己定义的而是在题目中总结出来的。
2.计算每一部分的时间复杂度
分:假设划分问题为a个子问题,每个子问题大小为n/b,则时间复杂度为D(n),即是关于n的函数。
求解:每个子问题和原问题的性质一致,原问题大小为n,时间复杂度为T(n),子问题大小为n/b,则子问题的时间复杂度为T(n/b)。有a个子问题,所以总时间复杂度为aT(n/b)。
合并:即将所有子问题的时间复杂度和并起来,共有a个子问题,所以合并的过程的时间复杂度也是n的函数假设时间复杂度为C(n)。
3.合并时间复杂度
T(n)=aT(n)+D(n)+C(n)
4.求解
利用递归方程的解法求解递归方程主要有三种方法。递归方程的解法可以参考算法设计与分析部分的上一篇博客,欢迎来我的创作中心逛一逛呀!
下面我们用分治法来解决下列问题:
3.最大最小值问题
1.问题描述
输入:数组A[1,2,3……]
输出:A中的最大值max和最小值min
2.常规思想
常规思想就是将第一个值赋为max,然后一个一个遍历,发现比max大的值就赋给max,min同理。对于一个有n个元素的数组,找最大最小值共比较了(2n-2)次。
3.用分治法改进算法一:
1.算法思想
首先来讲算法思想,我们将这组数据进行前与后两两比较。即比较A[0]和A[n-1],A[1]和A[n-2]依次类推,将两者中较大的放在后面,将两者中较小的放在前面,可以分成两个部分,再用常规思想进行遍历即可找到最大最小值。
2.图解
假设排序的数列为:6,10,32,8,19,20,2

首先两两进行比较,交换后得到下列数组:

其中最小值在红色框中出现,最大值在蓝色框中出现。
3.计算时间复杂度
若没有中间元素则一共需要遍历(n/2-1)*2次,在加上分组所需要的次数n/2,一共需要3n/2-2次。
如果有中间元素,则分组需要(n-1)/2次 ,遍历一共需要((n+1)/2-1)*2次,两者相加得到3n/2-3/2次。
无论哪一种都比原来的(2n-2)小,这就是分治法的作用。
4.伪代码实现
注意写伪代码之前要有声明
STATEMENT
input:数组A[1,2……n]
ouput:数组A[1,2……n]中的最大元素
For i<--1 TO n/2 DO
IF A[i]>A[n+1-i] THEN swap(A[i],A[n+1-i];//交换相对称的两个元素
max<--A[n],min<--A[1];
For i<--2 TO n/2(取上界) DO
IF min>A[i] THEN min<--A[i];//在第一个集合里找到最小值
IF max<A[n-i+1] THEN max<--A[n-i+1];//在第二个集合里找到最大值
print max,min;4.用分治法改进算法2:
1.算法思想:
将一组数两两分组进行比较,每组都要选出最大最小值,再将每组的最大最小值进行两两比较,得到下一轮的最大最小值,并递归下去,直到比较之后只剩下一个数,那么这个数就是该序列的最大或者最小值。
2.图解
通过解这道题发现了一个求递归函数的画图方法(机智如我):
假设要排序的数列为:6,10,32,8,19,20,2,14

这里每一个模块都代表了一次递归,如果类型完全相同(包括执行代码和返回值),则模块中的内容一样,如果不同则模块中的内容不同,即后面的四次是一样的类型,前面的三次是一样的类型,这么一看是不是很清晰呀。
3.伪代码实现
STATEMENT
input:数组A[1,2……n]
ouput:数组A[1,2……n]的max和min
MAX_MIN(1,n) //表示函数首先传的是1和n
MAX_MIN(low,high)
IF high-low=1 THEN
IF A[low]<A[high] THEN return (A[low],A[high]);
ELSE return (A[high],A[low]);//用于比较两个相邻元素的大小,是后四个模块的模型
ELSE
mid<--(high+low)/2;
(x1,y1)<--MAX_MIN(low,mid);
(x2,y2)<--MAX_MIN(mid+1,high);
x<--max{y1,y2};
y<--min{x1,x2};//用于进行递归比较,是前三个模块的模型
return (x,y);4.计算时间复杂度
假设整体的时间复杂度为T(n),一共分为了两组,所以每组的时间复杂度就为T(n/2),而最后还要进行两次比较所以时间复杂度为:
T(n)=2T(n/2)+2
根据递归树法求得
T(n)=3/2n-2
4.大数乘法问题
1.问题描述
输入:n位二进制整数x,y
输出:x和y的乘积
2.常规算法
二进制数乘法的法则为:
0×0=0
0×1=1×0=0
1×1=1
由低位到高位,用乘数的每一位去乘被乘数,若乘数的某一位为1,则该次部分积为被乘数;若乘数的某一位为0,则该次部分积为0。某次部分积的最低位必须和本位乘数对齐,所有部分积相加的结果则为相乘得到的乘积。
这里多说一下帮大家科普一下,假如说我们要计算的是4*7=28
二进制的乘法计算规则和整数是一样的:
列式:0100
* 0111
--------------------------
0100
0100
0100
-----------------------------
011100
即为28,这里将乘数的每一位都与被乘数相乘,最后结果再相加是一个θ(n^2)的算法。
3.分治法的初级改进
1.算法思想
 分别将x和y分为两个二进制集合,其中A与B,C与D的二进制位的个数相同。
分别将x和y分为两个二进制集合,其中A与B,C与D的二进制位的个数相同。
x*y=(A*2^(n/2)+b)*(C*2^(n/2)+D)=AC*2^n+(AD+BC)*2^(n/2)+BD
2.计算时间复杂度
此时要计算x*y就要计算AC,AD,BC,BD四个的值,假设T(n)是原式的时间复杂度,则AC,AD,BC,BD的时间复杂度均为T(n/2)。所以T(n)=4T(n/2)+θ(n),根据主定理求得时间复杂度为O(n^2)。
显然这不满足我们的需求,因为即使不使用分治法,计算的时间复杂度依然是O(n^2)。
4.分治法的进一步改进
1.算法思想
只要将第一步的x*y换一种写法:x*y=AC*2^n+((A-B)*(D-C)+AC+BD)*2^(n/2)+BD
2.计算时间复杂度
此时只需要计算AC,(A-B)*(D-C),BD即可,三者的时间复杂度为T(n/2),所以T(n)=3T(n/2)+θ(n),根据主定理计算出时间复杂度为O(n^(log(2)(3))比O(n^2)小,所以得到了满意的结果。
5.总结
我们发现一个式子经过不同的变换得到的时间复杂度是不同的,我们应该尽可能地减少乘法个数,增加加法或者减法个数,从而达到降低时间复杂度的目的。
5.棋盘覆盖问题
1.问题描述
在一块4*4的棋盘上插入方块组,其中棋盘上有一个方块部分不能被覆盖,一共有四种形状的方块可供选择,要求将除不能覆盖的地方全覆盖满。

2.用分治法思想分析问题
正方格棋盘是4*4的分布,所以我们可以想到将之分为2*2的棋盘,即分为四个部分。

我们要做的就是在这四个部分中,找到相同的思想来填充,即在每个模块中有且只能放一个方块组合,且会空出一个未被填充,所以在填充的时候只需要注意将三个未被填充的空间连在一起来使之能存放一个方块组。
注意我们应用的是分治法这一个方法,而不是我们思考怎么放方格组的过程,而是在思考之后放方格组这一行为算时间复杂度。即如何将未填充的方块放在中间连在一起这一思考过程并不算时间复杂度。
3.计算时间复杂度
我们将在空一块的2^k*2^k方格用四种不同形式的方格组填充这一过程的时间复杂度设为T(k),则我们需要将之分为2^(k-1)*2^(k-1)的四个方格组,每一个和原方格组一样需要空一格出来,所以性质是相同的,时间复杂度为T(k-1)。
所以T(k)=4T(k-1)+θ(1)
计算结果为T(k)=θ(4^k)
6.中位数问题
1.历史背景
选择中位数可以避免一组数据中最大值和最小值造成的影响,所以中位数也一直是人们乐于研究的问题,在历史上人们对它的上界和下界进行了多次的研究。

2.分析问题
求中位数本质上就是查找某个数组中第i大的数是哪个,所以转化成查找第i个数多大的问题。下面讨论如何在O(n)时间内查找n个元素中的第i个元素
input:n个数构成的集合X,整数i,1<=i<=n。
output:x∈X,且X中有i-1个元素小于x。
3.求解步骤
1.将整个数组五个一组分为n/5组。计算出中位数应该在排好序后的第i个位置。
2.通过插入排序求出每组的中位数。
3.将这些中位数排成一个序列,找到中位数的中位数x,并记录其下标k。
4.遍历整个数组,将比x的放在它的后面,比它小的放在前面。
5.如果i=k,则返回x。
如果i<k,则在第一个部分递归选取第i大的数。
如果i>k,则在第三个部分递归选取第(i-k)大的数。
4.图解
1.将整个数组五个一组分为n/5组。计算出中位数应该在排好序后的第i个位置。

2.通过插入排序求出每组的中位数。
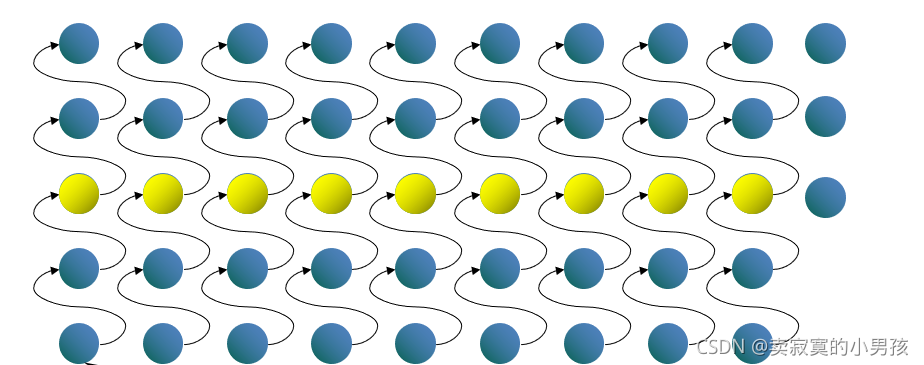
其中黄色的球为每一组的中位数。
3.将这些中位数排成一个序列,找到中位数的中位数x,并记录其下标k。

其中红色的球为这些中位数的中位数。即为x
4.遍历整个数组,将比x的放在它的后面,比它小的放在前面。
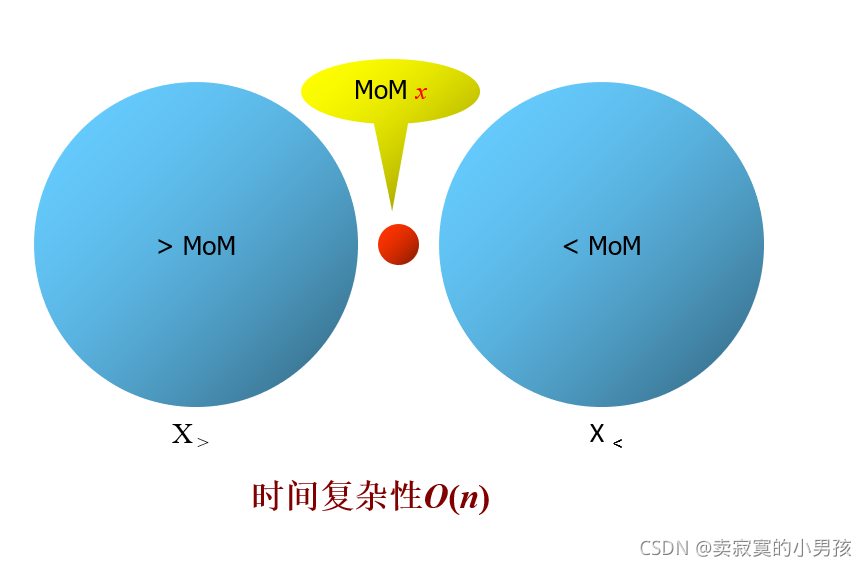
然后进行比较即可。
5.如果i=k,则返回x。
如果i<k,则在第一个部分递归选取第i大的数。
如果i>k,则在第三个部分递归选取第(i-k)大的数。
5.计算每一步的时间复杂度
假设在n个数中找中位数的时间复杂度是T(n)
1.θ(1)
2.排序每组数时,比较操作的次数为5(5-1)/2=10次,总共需要10*(n/5)(取上界,把不够5个的元素也算成了5个)次比较操作。时间复杂度为θ(n)
3.在n/5个数中寻找中位数,时间复杂度为T(n/5)(n/5取下界,因为多出来的不够5个的元素没参与比较)。
4.遍历整个数组的时间复杂度是θ(n)。
5.第五步相对来说比较复杂,而且是这个算法的核心,还是拿图说话:

我们已经将数据分为了三组,分别是比x大的数,比x小的数和x。
当x为第i个元素时,算法的复杂度就是θ(1)。
当x不是第i个元素时,我们就要在它前面的数据中寻找第i大的元素,或者在它后面的数据中寻找第(i-k)大的元素。这和我们在n个数中寻找第i大的元素是同一性质的,所以复杂度也可以用T()来表示。我们只要知道要查找的元素个数就可以将之表示出来了。
通过图我们可以看出,左边方框中的元素是一定比x大的元素,右边方框中的元素是一定比x小的元素。这些元素的个数为3*n/5/2(取下界)。即比x大的元素最多有n-3*n/10(取下界)个,比n小的元素最多有n-3*n/10(取下界)个,所以在这些元素中查找第几个数的时间复杂度一定不会超过T(7n/10+6)。
将这几步的时间复杂度加起来就是整个的时间复杂度:T(n)<=θ(n)+T(n/5)(取下界)+θ(n)+T(7n/10+6)
最终计算时间复杂度是小于O(n)的。
6.伪代码实现
input :数组A[1:n] //输入数组A有n个元素,:也可以表示‘到’的意思
output :A[1:n]中第i大的元素
Select(A,i)
For j<--1 TO n/5 DO
InsertSort(A[(j-1)*5+1],A[(j-1)*5+5];//利用插入排序寻找每一组中的中位数
swap(A[j],A[(j-1)*5+3]); //将所有中位数记录在数组A的前面
x<--Select(A[1:n/5],n/10); //在所有中位数中查找第n/10大的数,得到中位数的中位数x
k<--partition(A[1:n],x); //遍历数组A,将之分割成三部分,并找到x的坐标k
IF k=i THEN return x; //k为第i个元素则找到中位数x
else if k>i THEN return Select(A[1:k-1],i);//k>i在k之前寻找中位数
else THEN return Select(A[k+1:i-k); //k<i在k之后寻找中位数
7.排序的基本知识
分治法的优势在排序中有着重要的体现,用了分治法的排序,才是时间复杂度最低的排序。在讲解分治法对排序的影响时,我们先复习一下排序的基本知识。
1.排序的概念
排序是计算中经常进行的一系列操作,其目的是将一组“无序”的记录序列调整为“有序”的记录序列。简单来说 无序->有序。
通常情况下排序分为两种:内部排序,外部排序
1.内部排序
若整个排序的过程中不需要访问外存便能完成,则成这类问题为内部排序。
2.外部排序
若参与排序的数据数量过大,整个序列排序过程中不可能在内存中完成,则称此类排序为外部排序。
我们主要讨论的是内部排序的各种方法。
2.排序的流程
1.排序流程
1.得到n个记录数据的序列为{R1,R2,R3,R4,......,Rn}。
2.找到这组数据每个元素的排序关键字(即排序依据)为{K1,K2,K3,K4,......,Kn}。
3.利用函数对这些关键字进行比较发现{Kp1<=Kp2<=Kp3......<=Kpn}。
4.将记录数字的序列排序{Rp1,Rp2,Rp3,Rp4......Rpn}。
将这一流程称为排序的流程。
不要小看了这一流程,这是我们写排序代码时的步骤,可以让你忙而不乱地完成任务。
2.举例
假设要排序一组数据,数据中包含学生姓名和成绩连个成员,要按成绩从大到小排序。
1.罗列数据
(张三,89),(李四,55),(王五,79),(南宫问天,92),(东方铁心,100)
2.找到这组数据的关键字
89,55,79,92,100
3.写一个函数对这组关键字进行排序
100,92,89,79,55
4.对数据进行排序
(东方铁心,100),(南宫问天,92),(张三,89),(王五,79),(李四,55)
对于这种既包含关键字又包含其他成分的我们通常使用结构体来记录数据:
typedef define struct Record
{
char name[20];
integer score;
}Record;
Record R[5];
这里使用伪代码创立了一个存储数据元素的结构体,关于伪代码的写法可以逛逛我的博客呀!以后在算法的这一部分我尽量都用伪代码,方便学习各类语言的人都可以看懂(是不是很nice)。
3.内部排序
1.内部排序的特点
在排序的过程中,参与排序的记录序列中存在两个区域:有序区和无序区。内部排序的过程是一个逐步扩大记录的有序序列长度的过程。
使有序区中记录的数目增加一个或几个的操作称为一趟排序。
举个简单的例子
假如对 3,1,6,8从大到小进行排序1,6,8就是一个有序序列,我们需要逐渐扩大这一有序序列,将有序序列的三个数变成4个数,就要将3和1调换位置,此时有序区数字增加了一个,所以该行为称为一趟排序。
2.分类
我们根据逐步扩大记录有序序列长度的方法有如下几类:
1.插入类:将无序子序列中的一个或几个记录“插入”到有序序列中,从而增加记录的有序子序列的长度。这一类排序有“直接插入排序”和“希尔排序”。
2.选择类:从记录的无序子序列中“选择”关键字最小或最大的记录,并将它加入到有序子序列中,以此方法增加记录的有序子序列的长度。这一类排序有“简单选择排序”和“堆排序”。
3.交换类:通过“交换”无序序列中的记录从而得到其中关键字最小或最大的记录,并将它加入到有序子序列中,以此方法增加记录的有序子序列的长度。
4.归并类:通过“归并”两个或两个以上的记录有序子序列,逐步增加记录有序序列的长度。
5.其他:比如还有一些基数排序的方法等。
4.基于分治法的排序算法
主要有归并排序和快速排序两类。
mergesort(归并排序):选择一个位置将数组划分为两个部分。
quicksort(快速排序):选择一个划分标准,根据元素与该标准的大小关系进行划分。
不同的划分策略对应不同的合并策略。
8.归并排序(Mergesort)
1.含义
所谓归并排序是指将两个或两个以上有序的数列(或有序表),合并成一个仍然有序的数列(或有序表)。这样的排序方法经常用于多个有序的数据文件归并成一个有序的数据文件。
这是百度上给的定义,简单地说就是先将元素分为两两一组,比较大小,在逐渐合并,每一次合并后的元素都是有序的。
归并排序的求解是要从下向上进行的,但由于我们进行的是算法分析,所以整个过程是从上向下分析的。
2.图解
假设要排序一组数2,4,1,8,5,9,7,3

再说一下比较的过程,由于这不是算法重点,就不画图了,以1 2 4 8和3 5 7 9为例。
首先定义指向1和3的指针,比较1和3的大小,把小的排在前面,然后将小的部分的指针加一。
3.伪代码实现
input:A[i:j]
output:排序之后的A[i:j]
Mergesort(A.i,j)
k<--(i+j)/2;//找到数组A中的中间值k作为分隔
Mergesort(A,i,k);//将前一半进行归并排序
Mergesort(A,k+1,j);//将后一半进行归并排序
l<--i,h<--k+1,t<--i//定义指针l和h分别指向两个排好序的序列的第一个元素
While (l<=k AND h<=j) DO
IF A[l]>=A[h] THEN B[t]<--A[h];t++;h++;
ELSE THEN B[t]<--A[l];t++;l++;//将两组数进行合并排序
IF l<k THEN
FOR v<--l TO k DO
B[t]<--A[v]; t++;
IF h<j THEN
FOR v<--k+1 TO j DO
B[t]<--A[v]; t++;//当第一组或第二组数个数多时,将多余的元素按顺序插入到末尾4.计算时间复杂度
我们在计算时间复杂度时一定要先想到这里用到的是分治法,所以书写算法复杂度的方程时,一定是用递归的形式来书写的。
这里把将n个数进行归并排序的时间复杂度记为T(n),那么n/2个数进行归并排序的时间复杂度就是T(n/2),将两组数比较的次数不超过n次,(一般没有明确的比较次数的与数据量有关的时间复杂度中一定有n),所以剩余部分可以记为O(n)。
所以T(n)=2T(n/2)+O(n),根据主定理计算出时间复杂度为O(nlgn)。
9.快速排序1(Quicksort:Partition)
1.含义
快速排序两种方法都应用到了分治法,Partition算法是其中的一种,即先确定一个划分标准x(通常为第一个元素),将数组中小于x的元素放在数组的前一部分,大于x的元素放到数组的后面部分,并返回一个划分k,并进行递归求解。
2.图解
假设要排序一组数据7,3,4,9,2,8,这里的x是第一个元素。定义一个指向首元素的指针p和指向尾元素的指针q,当p指针++找到比x大的元素时停下来,当q指针--找到比x小的元素时停下来,并交换两者指向的元素,直到q<p此时q前面的元素(包含q)比x小,p前面的元素(包含p)比x大。返回q的值,进行下一次递归。

注意出于对函数的整体实现的考虑,为使每次使用函数时都一样,所以第一次没有进行任何比较的时候就需要交换一次。

第一次交换后发现p指向的元素大于是8大于x,所以p不动,q指向的是7>=x,所以q--,之后q指向的元素是2所以q不动。

第二次交换后,p指向2比7小所以p++,直到p指向9比7大所以停下来。q指向8,比7大,q--直到q指向4,比7小所以停下来。
此时q<p,所以q前面的元素(包含q)比7小,p后面的元素(包含p)比7大,返回q的值,再进行比较即可。
理解这段内容的关键就在于以每一次交换为一个周期,了解每一次交换之后发生的事情。
3.伪代码实现
注意需要两个函数来实现,分别是总框架partitionSort和分组函数partition
partitionSort(A,i,j)
input: A[i……j],x
ouput: 排序之后的A[i……j]
x<--A[i];
k=partition(A,i,j,x);//k来接收返回的q指针
IF(k==i) THEN return;//当q与i相等时停止。
partitionSort(A,i,k);//对q前面的元素进行分组
partitionSort(A,k+1,j);//对q后面的元素进行分组
partition(A,i,j,x)//进行分组
p<--i;q<--j; //两指针就位
While(p<q) DO
swap(A[p],A[q]);//每次交换算一个周期
While(A[p]<x) DO
p<--p+1; //p指针++直到找到比x大的元素,停下来
While(A[q]>=x) DO
q<--q--; //q指针--直到找到比x小的元素,停下来
return q;4.算法复杂度分析
1.最好情况
这一情况是最不重要的情况,在partition算法里,最好的情况是数组每次都能被分为大小相等的两部分,设分隔m次,所以n/(2^m)=1,所以m=log(2)(n)。每一轮都需要θ(n)次比较,所以时间复杂度为θ(nlog(2)(n))。
均分是最好情况的原因是,无论分几次,比较的次数都是θ(n),所以只与分隔几次有关,对于一组n个元素的数组,将它们分成零散的元素,分隔次数最少的方法就是每次都进行均分。
同时分隔次数最多的方法就是每次都1个一个分,即为最坏的情况。
2.最坏情况
按一个元素一个元素来分,将每次比较的次数加起来得到时间复杂度为
(n-1)+(n-2)+……+1=n(n-1)/2=θ(n^2)
3.平均情况
平均情况即分隔点是任意找的,也是我们最经常遇到的一种情况。
设分隔点是第s大的元素

我们将s考虑到每一种情况,即分隔点可能是第1大,第二大,第三大。。。的元素,对每一种时间复杂度求和取平均得到平均时间复杂度。再加上第一次分隔时比较的次数cn,cn和n是同一个含义。但我们习惯于加一个系数。
展开
T(n)=1/n(2T(1)+2T(2)+......2T(n-1)+T(0)+T(n))+cn //注意这里T(0)=0所以可以删去
(1) (n-1)T(n)=2T(1)+2T(2)+......2T(n-1)+c(n^2)
(2) (n-2)T(n-1)=2T(1)+2T(2)+......2T(n-2)+c(n-1)^2
(1)-(2)得到
(n-1)T(n)-nT(n-1)=c(2n-1)
则:T(n)/n=T(n-1)/(n-1)+c(1/n+1/n-1),根据递归树法
T(n)/n=c(1/n-1/(n-1))+c(1/(n-1)-1/(n-2)+……c(1/2+1)+T(1)
=c(1/n+1/(n-1)+……1/2)+c(1/(n-1)+1/(n-2)+……1)
H[n]=1+1/2+1/3+1/4+……1/n
根据调和级数公式H[n]=O(logn)
T(n)/n=c(H[n]-1)+cH[n-1]=c(2H[n]-1/n-1)
T(n)=2cnH[n]-c(n+1)=O(nlogn)。
10.快速排序2(Quicksort:PartitionRundom)
1.含义
作为快速排序的另一种方式(和原来的一样,注意不是填坑法,否则我就写dig a hole了),这里的划分方式和之前的不同,之前的是将第一个元素作为划分点,这里是随机产生一个元素作为划分点,即将k的值在i到j中随机产生。
2.伪代码实现
和之前的一样,只不过随机产生k.
partitionSort(A,i,j)
input: A[i……j],x
ouput: 排序之后的A[i……j]
temp<--random(i,j)//在i与j之间产生一个随机数
x<--A[temp];
k=partition(A,i,j,x);//k来接收返回的q指针
IF(k==i) THEN return;//当q与i相等时停止。
partitionSort(A,i,k);//对q前面的元素进行分组
partitionSort(A,k+1,j);//对q后面的元素进行分组
partition(A,i,j,x)//进行分组
p<--i;q<--j; //两指针就位
While(p<q) DO
swap(A[p],A[q]);//每次交换算一个周期
While(A[p]<x) DO
p<--p+1; //p指针++直到找到比x大的元素,停下来
While(A[q]>=x) DO
q<--q--; //q指针--直到找到比x小的元素,停下来
return q;3.算法性能分析
这里和第一种并没有什么复杂度的差别,只不过换了一种算法的分析方式,分析的目的在于计算算法的平均复杂度。
1.定义
1.定义S(i)代表第i大的元素,则最小的元素为S(1),最大的元素为S(n)。
2.当在程序执行是S(i)和S(j)发生比较时,记为X(ij)=1,若没比较则X(ij)=0。
2.分析
1.算法比较的总次数为所有元素的比较次数之和:
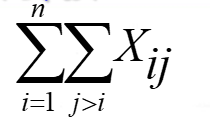
i表示将所有数据都遍历一遍,j表示与第i个元素相比较的元素个数,即一个i对应固定个数的j
2.算法的平均复杂度要使用数学期望来表示:

计算E[X(ij)]=p(ij)*1+(1-p(ij))*0=p(ij)
其中p(ij)表示的是S(i)与S(j)比较的概率,所以计算平均复杂度问题就转变成了求S(i)与S(j)发生比较的概率的问题。
3.求解p(ij)
我们可以用树来理解这一问题,即在n个数中p(ij)的值是多少。

通过观察我们发现:
1.当S(i)与S(j)发生比较时,S(i),S(i+1),S(i+2)……S(j)一定在同一个树中。
2.只有在S(i)或者S(j)为被选中的参照值时,两者才会比较。
满足这两个条件即可,总结出来就是在S(i)到S(j)这些数中,选中S(i)或者S(j)的概率之和。
p(ij)=2/(j-i+1)。

所以快速排序的平均时间复杂度就为O(nlogn)。
11.排序问题的下界
1.含义
我们考虑一个算法的优劣通常是用最坏情况和最优情况来衡量的,最优情况基本没什么用。
本内容主要证明比较排序最坏情况和平均情况的时间复杂度的下界的极限是Ω(nlogn),不可能写出时间复杂度比nlogn低的排序。即如果一个排序的时间复杂度为nlogn,那么这个排序算法是最优的,不可能再找出比它更好的排序算法。
比较排序:在排序的最终结果中,各元素的次序依赖于它们之间的比较,我们目前学的所有排序算法都是比较排序。
我们以为三个元素排序为例,即为1,2,3这三个数字排序。
一个算法的复杂度不是确定的,分为最优,最坏,平均三种,每一种情况都对应了一个上界和一个下界。你可能会说一个算法的最优解的比较次数不是固定的吗?那时间复杂度应该也是固定的啊。但是输入数据的n在改变,是n的大小导致了三种情况的上下界问题。
2.最坏情况下排序的下界
1.引入
为1,2,3这三个数字进行排序,这三个数字的初始位置无非只有六种
1,2,3
1,3,2
2,1,3
2,3,1
3,1,2
3,2,1
我们可以画出插入排序的决策树:

也可以画出冒泡排序的决策树:
 无论按哪一种排序方式来画,最终每一个叶子节点对应一种1,2,3的排序方式,即这种排列方式经过从根节点到叶子节点这一过程完成排序。也就是说这样一棵树依赖于叶子节点得以建立。
无论按哪一种排序方式来画,最终每一个叶子节点对应一种1,2,3的排序方式,即这种排列方式经过从根节点到叶子节点这一过程完成排序。也就是说这样一棵树依赖于叶子节点得以建立。
首先我们明确要找的是最坏情况的下界,即对n个数进行所有排序算法中,由于n个数排列不同而导致比较次数最多的情况的下界。(吐槽一下ppt老师做的有问题,我发现了,但是老师估计永远不会去看这篇博客)。
听起来很绕啊,再来解释一下:我们要明确几个点才能证明:
2.证明
1.所有比较排序算法的决策树都可以抽象成一棵决策树,(观察上面两幅图发现两者是一样的),并且这个决策树一定是一棵完全二叉树。
2.我们要找的是每一个排序算法的最坏情况对应的时间复杂度。
3.我们要证明这些时间复杂度都为Ω(nlogn)。
4.无论什么算法,有n个数那么就有n!个形式,每种形式对应一种排序过程。注意每一个节点是一次比较,我们要找的最坏情况就是比较次数最多的情况(注意最差情况不止一种),即树高。
5.每一种排序的最坏情况是可以计算出时间复杂度的,用O阶什么的表示就是为了涵盖多种情况。
了解了这些就可以把计算排序中最差情况抽象成在一棵有n!个叶子节点的完全二叉树中,计算树高h的问题。
完全二叉树是满二叉树最后一行删掉一些元素,所以n!<=2^h
计算求得h>=lg(n!),我们要求h的下限,即求lg(n!)的最小值。
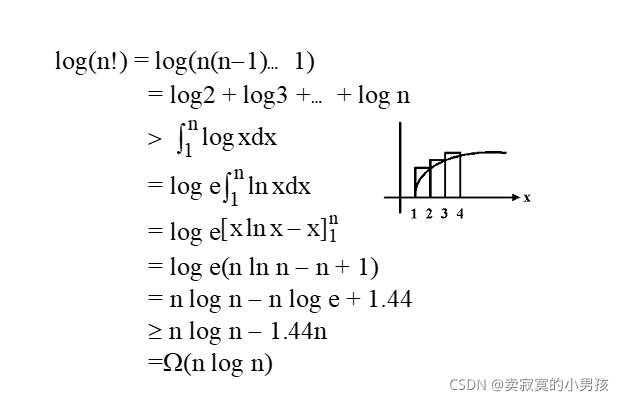
还想再说点:h已经是最坏的情况了其实我们就是通过n!与2^h的逼近程度区分不同算法的,但即使有区分,每种算法最坏情况的时间复杂度一定>nlogn。我们发现归并排序和堆排序的算法的上界是O(nlogn)所以他们是最优算法。复杂度为θ(nlogn)。(竟然如此之细致,表扬自己一波)
3.平均情况时间复杂度的下界
1.引入
如果你已经理解了最坏情况下的时间复杂度的下界,那么也很容易理解平均情况下时间复杂度的下界,从根节点到叶子节点的最长路径对应最坏的情况,那么从根节点到所有叶子节点的路径和再除以路径条数就表示平均情况,我们可以计算出它的值。
2.证明
1.假设这是一颗有c个叶子节点的二叉树,深度为d,由于决策树是完全二叉树,所以叶子节点仅仅出现在第d层和第d-1层。
2.假设x1个节点在d-1层,x2个节点在d层。
那么就可以得到:
x1+x2=c
x1+x2/2=2^(d-1)
可以推出:x1=2^d-c
x2=2(c-2^(d-1))
再经过一系列的运算:

这就证明出来了平均的时间复杂度的下界也是nlogn。
12.思考题1
1.题干
给定单调不减数列a0....an和一个数k,在O(logn)的时间复杂度内找到满足ai>=k的最小i,写出伪代码。
2.求解
由于是已经排好序的,所以直接寻找中间值即可。
input:A[0...n],k
ouput:i
Lowbound(A,k)
lowbound=0;
upbound=A.length-1;
While upbound-lowbound>0 DO
mid=(lowbound+upbound)/2;
IF A[mid]>=k THEN
upbound=mid;
ELSE lowbound=mid+1;
print upbound;就是找中间值然后比较就可以了。
每次都比较的是一半的元素,写出表达式
T(n)=T(n/2)+O(1),根据主定理计算出时间复杂度为O(logn)。
13.思考题2
1.题目
给定一个平面内的n个点,用O(nlogn)的时间复杂度求出距离最近的两个点,写出伪代码。
2.求解
假设给定5个点:A1,A2,A3,A4,A5,使这五个点的x值逐渐增大的。
1.首先根据中间值将x轴划分成两部分

2.继续划分子问题,将A1到A3作为一个整体,找到中间值A2

3.此时只剩下三个点了,计算左侧最短距离d1,即A1与A2的距离;和右侧最短距离d2,即A2与A3的距离,计算两者的最小值为d。此时A2的左右两侧的最小值已经找到了,现在的问题是在A2点的周围,一个左侧元素和一个右侧元素的距离是否可能小于d。
4.以A2的横坐标x2为分隔点,寻找横坐标在(x2-d,x2+d)的元素。因为只有在这个范围内的左右两侧元素才有可能距离是小于d的。

5.此时在(x2-d,x2+d)中涵盖了一些点,对于这些点来说,以A1为例,为了寻找右侧的与它距离小于d的点,那么两者的纵坐标之差一定小于d,所以找出范围内所有点的(纵坐标-d,纵坐标+d)这一范围的点,计算两者之间的距离d',与d比较看是否小于d,如果小于则d=d'。此时的含义为在A3右侧的点的最小值是d',我们又可以计算A3左侧元素的距离最小值,两者再比较从而形成了递归。

3.伪代码实现
input:A[1……n]
output:最小值d
closest_pair(A)//计算整体的最小距离
If A.size<=1 return INF//当
sort_by_x(A) //将数据按横坐标大小进行排序
m = A.size/2; x= A[m].first //找出数据的中点,将其x坐标赋值给x
d = min(closest_pair(A[0..m]),closest_pair(A[m+1..n]))//计算两侧的最小距离d
sort_by_y(A)//将A按纵坐标大小排序
For i = 1 to n
If A[i].first-x>=d continue;//当A[i]的横坐标与x的距离大于x时,进行下一次循环
B.push(A[i])//定义一个B数组,用于接收A数组按纵坐标排序后且在2d范围内的元素
for j=0 to b.size //当j从0到n
dx = A[i].first – B[b.size-j].first//计算x的差值
dy = A[i].second – B[b.size-j].second//计算量元素y的差值
If dy>=d break //当dy>d时,跳出这一次循环,说明两者的距离一定大于d
d = min(d,sqrt(dx*dx+dy*dy))//计算d与两者距离的最小值赋值给d
Return d4.计算时间复杂度
找n个元素的距离最小值是T(n),那么找一半元素的最小值就是T(n/2)
所以T(n)=2T(n/2)+O(1)
根据主定理,T(n)=O(nlogn)。
13.总结
突破记录了,目前写的字数最多的文章,但我感觉动态规划的话会更多,写完之后的感觉还是“我原来可以这么细”,当然如果你比我更细的话,,欢迎私信我啊,让好奇的我看一看“戏中戏”是什么样子的啊。分治法是一种设计算法的思想,它的优秀程度以及如何熟练使用也是需要进行不断地练习才能感悟。


























 474
474

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










