[普通物理] 振动的能量和振动的合成

慕梅^

已于 2022-06-21 12:38:08 修改

阅读量2k

点赞数

分类专栏：普通物理文章标签：普通物理

于 2022-06-20 01:10:13 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_51533157/article/details/125340382

版权

普通物理专栏收录该内容

8 篇文章

订阅专栏

本文探讨了简谐运动中动能和势能的周期性变化，强调在弹簧振动过程中，动能和势能如何在最大值和最小值之间转换。在平衡位置，动能达到最大，势能为零；而在最大形变处，势能最大，动能最小。平均动能和势能与总机械能的关系也得以阐述，它们均等于总机械能的一半。此外，文章还提及了频率的概念及其在振动合成中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.振动的能量

1.1动能和势能的周期

这里直接给出结论：
在这里插入图片描述

1.2动能和势能的变化过程

在这里插入图片描述

此时弹簧压缩达到最大，此时弹性势能达到最大，而动能为0

此时物体到达平衡位置，这时弹簧的形变为0，那么弹性势能为0，动能达到最大

在这里插入图片描述

此时弹簧拉伸到最大，形变量也是最大，此时弹性势能为最大，动能为最小

整体来说，不考虑能量损失，就是弹性势能和动能之间的相互转化

1.3 平均动能和平均势能

在这里插入图片描述
图：

其中粉红色为位移曲线，而势能和动能的曲线的周期为简谐运动的一半（途中可以看出）
而当粉红色达到最高点，意味着位移达到最大值，此时应该是势能最大，而位移为零时，此时的动能最大。
当他们到达最大时，等于总机械能，他们的平均势能和平均动能都为总机械能的一半。

2 同一直线上同频率的谐振动的合成

频率是单位时间内完成周期性变化的次数，是描述周期运动频繁程度的量，常用符号f或ν表示，单位为秒分之一，符号为s-1。为了纪念德国物理学家赫兹的贡献，人们把频率的单位命名为赫兹，简称“赫”，符号为Hz。

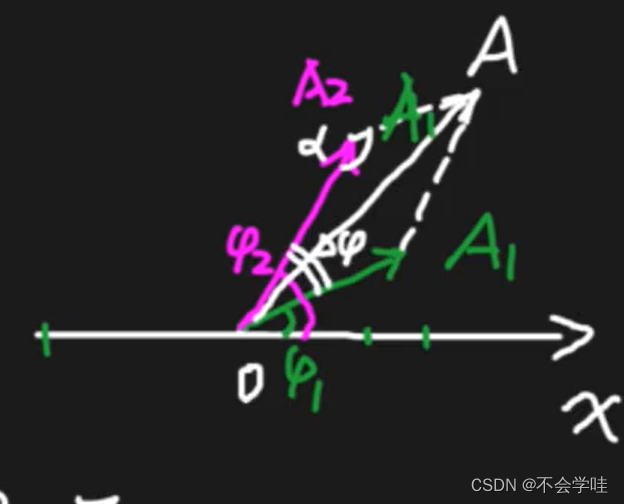
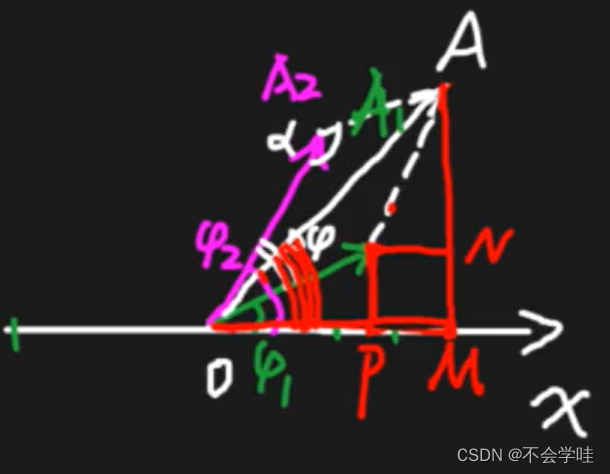
在这里插入图片描述

在这里插入图片描述

习题

在这里插入图片描述

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。