离散数学复习

第一章

命题必须是断言
**仅当-> 1 -> 0 才为假 ** 仅当后面为结果，例如仅当A，B 为B->A

当且仅当<->，第一个当表示充分条件，第二个表示必要条件

重言式（永真式） 矛盾式（永假式）既不是重言式也不是矛盾式，叫偶然式

所有指派全为真则为永真式，if有->则为永真蕴含式,if是<->则为永真式

证明永真蕴含式，前真则后真，后假则前假

情况并非如此 就是在加个非

用非和与表示可以先求出用或表示的表达式，再非一下

有的式子化简结果不等，可以 与（P或非P）

对偶规则：不会改变变元，非不变化， 只变与，或，量词

析取范式：基本积之和
合取范式：基本和之积
P既是基本和也是基本积

极小项：在基本积中，每个变元必出现一次，且仅出现一次，n个变元有2的n次方个极小项

极小项之和为主析取范式，加非为0，反之为1
注意补全

极大项：在基本和中，。。。
非为1，反之为0

注意！！！求出主析取范式之后，直接就数字就可以找主合取范式，例如主析取范式{0,1,2,7} 主合取范式就为{3,4,5,6} ,数字不一样，但范式里的每个变元的非情况可能相同

P29 CP规则，证明蕴含式可能会用到

反证法 很有用P30 将结论取反当作条件使用，最终证明出A与上非A即可

个体：张三 3等 代表个体的变元位个体变元
谓词描述个体性质或者个体间的关系，有几个个体变元就是几元谓词
论述域：个体变元的取值范围位个体域空集不能作为论述域
命题是0元谓词
在谓词前进行量化后，命题的真假与论述域有关（先看论述域）！！！
存在y，y=3 不一定为真，如果论述域>3，就是错的
全总个体域：包含所有个体

针对全总个体域，M(x)是人，是特征谓词（刻画论述对象具有人的特征）特征谓词加入断言中有两个条件：（P37）
对于全称量词，特征谓词作为蕴含式前件加入
而对于存在量词，作为合取式加入

原子公式：不含命题联结词（非，与，或等）

紧接量词后的最小子公式为量词的辖域

存在x，或者任意x时，辖域内的x（注意必须是x，如果辖域内出现y但没有存在y等，y仍是自由变元）为约束变元，辖域外的为自由变元。

否定词可通过量词深入辖域

证明式子不等价，可以用直接举反例

注意量词辖域的扩张与收缩 量词分配的恒等式（任意与，存在或为恒等式） CP规则 Q1

量词的次序很重要！

改名规则只能用于约束变元，代入规则只能用于自由变元（原式为永真式，代入仍是永真式，原式为非永真式，代入可能变化）。

去量词时，该量词必须是公式的最左边的量词，且此量词的前边无任何符号， 它的辖域作用到公式末尾。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oSwActYF-1654527431830)(C:\Users\fanshihao\AppData\Roaming\Typora\typora-user-images\image-20220526210931066.png)]

US :

ES: 不能是前面推导的自由变元，也不能是ES本身引入的表面自由变元

EG:

UG: 1. x都不是自由的，也不能是由ES引入的 2. 如果US引入自由变元x后，ES引入新变元y且自由出现，则不能用UG

US和ES用于删除量词，使用ES而产生的变元不能保留在结论中，因为这只是暂时的假设

如果推导过程中既要用US又要用ES,则先处理存在ES,在使用US

集合和二元关系

集合的并和交是可交换，可结合具有分配率

自然数(0,1,2,3…)N 正整数N+

实数R

整数I

五种运算 并 交 差（-） 补

n个元素的集合A，其**幂集（集合A中所有子集的集合）**的元素个数为2的n次方

n重组的第一个分量为n-1重组

集合的笛卡尔乘积运算不可交换，也无结合律

自反：集合中的每一个元素，自己都和自己存在关系（关系矩阵对角线都为1）

反自反：集合中的每个元素，都和自己没关系（对角线都为0）

有些既不是自反，也不是反自反

对称：对任意两元素，既有xRy，又有yRx（关于对角线对称）

反对称：对任意两元素，没有xRy，又有yRx（如果aij=1且i != j，则aji=0，但如果aij=0，不一定aji=1）

空关系既是对称又是反对称，相等关系也是（aij没有等于1的）

传递：如果xRy, yRz，有xRz（关系矩阵无规律） 但如果前件为假（R{<1,2>,<1,3>}，找不到xRy和yRz），则也具有传递性

相等关系：自反，对称，反对称，传递但不反自反

非空集合的空关系（非空集合中有元素属于A，所以自反和反自反的前件都为真（自反的条件为），其余前件都为假）：反自反，对称，反对称，传递，但不自反

空集合的空关系（没有元素属于空集合（不含任何元素的集合为空集合空集合不包含空集），所有前件都为假）：自反，反自反，对称，反对称，可传递

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NVYmlnBk-1654527431831)(C:\Users\fanshihao\AppData\Roaming\Typora\typora-user-images\image-20220527171548074.png)]

关系的合成满足结合律

关系矩阵乘法可结合

逆关系：关系R是从A到B，而逆关系则是从B到A的关系

空关系的逆还是空关系

3.4次序关系

偏序集合：自反，反对称，传递

为什么哈斯图可以表示偏序关系：偏序关系具有反对称性，所以可以用无向图来表示，而且又有传递关系，不用画多余的传递边

哈斯图画法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IS7vi0By-1654527431832)(C:\Users\fanshihao\AppData\Roaming\Typora\typora-user-images\image-20220527191654471.png)]

哈斯图的画法，以及利用哈斯图寻找极大元之类 - 知乎 (zhihu.com)

确定最大元最小元之前，先判断极大元和极小元：在子集B中，最上面一行为极大值，最下面一行为极小值，且都不唯一

再判断最大元和最小元：如果极大（小）值唯一，则最大（小）值存在，否则不存在

最大元最小元如果存在，那必唯一

上界和下界：注意两者必须有关系！！！，如{6，12，24}的上界没有36，因为和24无关

注意！！！所选的上下界都必须和子集中的所有元素有关系，可能不是子集的，也可能包含子集

极大元极小元一定存在 最大元，最小元，上下界不一定存在

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yNSUyvlo-1654527431834)(C:\Users\fanshihao\AppData\Roaming\Typora\typora-user-images\image-20220527193458015.png)]

最小上界和最大下界：上界里面最小的和下界里面最大的

如果有最大元，则一定是最小上界，最小元同理

子集为{2，6，8}时

上界为24 12，36不是上界，因为都和8没有关系

下界为1 2 3和2，8无关，不是

拟序集合：集合A上的二元关系R是反自反，反对称，传递 例如实数集合中的<关系

线序集合：对于偏序集合A中，任意两个元素都有关系 哈斯图就是一条链，无分支

良序集合：A上的二元关系R是一线序，则A的每一个非空字节都有最小元素（极小元素存在且唯一），则R叫做A的良序。

每个有限线序集合是良序的

3.5等价关系

等价关系R是自反，对称，传递的。

模k等价：其含义为等价类里面的任何数，模k之后都相等。k为几就有几个等价类

等价类：与集合A中x具有R关系的y的组成集合，其中R是等价关系

不同等价类的个数称为R的秩
集合A的等价关系，要么相等，要么不相交

集合的覆盖与划分

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ylBKvdVS-1654527431835)(file:///C:\Users\fanshihao\Documents\Tencent Files\1360532588\Image\C2C\Image1\7S3DXDIHU8C535ZC8_T%}7.png)]

代数

第六章 代数

单射函数（一对一，但B中可以有多余元素没有被A指向，但如果指向了必须只有A中的一个元素指向B）：


满射：B中元素都有至少一个相对的A的元素

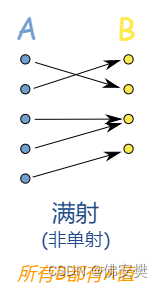
双射：满足单射和满射，真正意义上的一对一

代数是一集合，运算封闭，具有代数常元

幺元与任何元素运算都是其元素本身

零元与任何元素运算都是零元 零元不存在逆元

左右幺元是对集合中是所有元素来说的

左幺元和右幺元相等则存在幺元，顺序搞清楚

零元同理

一个运算的幺元和零元是唯一的

逆元：xy=1，x是y的左逆元，y是x的右逆元，1是幺元
若xy=1 y*x=1同时成立则x是y的逆元（y也是x的逆元）

对于每一个元素，如果元素存在逆元，则唯一

可逆一定可约，但可约不一定可逆

子代数运算封闭，基本是原集合的子集，代数常元在子集中，但原集合的代数常元不一定是子集的代数常元

子代数一定存在，最大是它本身

6.3 同态

同态：存在一双射函数h

映射h为A到A撇的同构（双射函数）

A与A撇同构，ARA撇，R是二元关系

若h不是双射函数，只是一普通函数，其余与同构条件相同，则h是从A到A撇的同态

若h是单射函数，则称h为单一同态

若h是满射函数，则称h为满同态

双射就是同构

若A=A撇 则称h为自同态

若A=A撇并且h是同构 则称h为自同构

6.4 同余关系

同余关系是等价关系的一种,它需要具备等价关系的特点，即传递，对称，自反除了具有等价关系的特点，还需要有已知a_b，则a*cb*c且c*a~c*b，*是代数A中的关系

相等关系是任何代数上的同余关系

6.6 半群和独异点

具有结合律的代数称为半群 子半群是半群

半群含幺元称为独异点（含幺半群） 子独异点也是独异点

加法和乘法符合结合率，减法和除法不符合（不一定，主要看集合）

若运算可交换，则为可交换半群

在任何可交换独异点S中，S等幂元素的集合T可构成子独异点

在半群中，等幂元素可能不止一个，但在群中，幺元是唯一等幂元素

生成元（不是幺元，但幺元为生成元的0次幂） 如果在独异点中，存在一个元素a属于S，a可以表示S中其余任何元素，则该独异点为循环独异点，a为生成元，由生成元生成循环独异点。

并不是所有的独异点都具有生成元。但循环独异点都是可交换的，即为可交换独异点

独异点的子半群（只要求集合T属于S就行）可以是个独异点

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5eu2E5Kj-1654527431836)(C:\Users\fanshihao\AppData\Roaming\Typora\typora-user-images\image-20220604181246928.png)]

群中只有幺元是等幂的。

6.7 群

群的定义：除了具有半群（可结合）和独异点（存在幺元）的性质外，还具有一性质：每个元素都存在逆元的代数系统

群还具有消去律

幺元是群中唯一的等幂元

所以如果有零元则一定构不成群，因为零元没有逆元

如果还具有可交换的性质，则为可交换群或者阿贝尔群

群的阶数为群中元素的个数，元素的阶数为元素a^k=e的k的最小值（元素和逆元具有相同的阶数

{e,a^1,a2}则该群为三阶，因为e=a^3

置换群定义：n个元素组成的集合A，(置换有n!个)，A上的置换（不一定是所有置换）所构成的群称为n次置换群，所有置换所构成的群为n次对称群

循环群：循环群是由g生成的，g为生成元。循环群是可交换群 类比于循环独异点（不同点是幺元是生成元的0次幂） 生成元都不一定为1个

if G为有限循环群 并且 |G| = n 则 g^n=e

子群

图论

在有向图中，任意两个结点，至少有一个结点能直接到达另一个结点，则为单向联通

若任意两结点都互相可到达，则图为强连通

若任意两结点不能相互到达，但把方向去掉，可联通，则为弱连通图

欧拉图的判定：无向连通图，顶点次数都为偶数

判断是否存在欧拉路径：该无向连通图存在0个或者两个奇次次数的顶点

哈密顿图