【基于R语言群体遗传学】-7-遗传变异（genetic variation）

一些新名词

Continuous time: 连续时间，是指不间断流动的时间，不以单位时间形式出现。

Diffusion: 扩散，是指粒子从高浓度区域向低浓度区域的被动净移动。

Discrete time: 离散时间，是指被划分为单位的时间，例如每个世代。

Genetic drift: 遗传漂变，是指由于进化抽样误差导致的等位基因频率的变化。

Factorial: 阶乘，是指从某个正整数开始，所有小于或等于该数的正整数的乘积，用 ! 表示（例如，4! = 4 × 3 × 2 × 1 = 24）。

Transition probability: 转移概率，是指从一个状态转变到另一个状态（或保持在同一状态）的概率。这些概率通常被组织成一个包含所有可能状态的矩阵。

遗传漂变与进化采样（Genetic drift & evolutionary sampling）

基本知识

计算群体遗传学的一个核心理念是，在群体中观察到的预期遗传变异的绝大多数将归因于看似随机的变化，而不是直接进化选择的结果。这个基本理念很简单：生物体有时会因为随机的机会而死亡或不繁殖，而其他生物体可能因为机会而比平均水平产生更多的后代，这影响了通过世代传递的遗传变异。群体遗传学学科的创始人之一，Sewall Wright，早在1929年就提到，等位基因频率似乎在世代之间“漂移”，从一个频率到另一个频率，而没有朝着在群体中固定或灭绝的方向进行稳定。“遗传漂移”这个词一直沿用至今。中性突变（而非自然选择明确驱动的变异）构成了观察到的遗传变异的大部分，这一观点最早由Motoo Kimura在六十年代正式提出，并仍然是统计分析群体中观察到的遗传变异的关键考虑因素。中性变异理论的重要性在于，它为观察到的遗传变异提供了一个简洁的预期，因此提供了一个简明的零假设，用以检验替代假设。就像之前我们为了预测等位基因和基因型频率之间的相互作用而做出了一系列假设一样，为了定量地研究等位基因频率随时间的随机变化，通常需要就几个起作用的因素做出许多假设。例如，变异是如何精确地通过世代传递的？新突变的发生和迁移带来新变异的情况又如何？可以做出的考虑几乎是无穷无尽的，但为了使问题可管理，我们将只假设几个简单的事实：

1. 生物体的世代不重叠（一代死亡，下一代出现）。

2. 生物体是二倍体（每个个体都有两个基因拷贝）。

3. 种群大小固定（N），跨代不变。

4. 每个等位基因都是随机“抽取”的，独立于所有其他等位基因，从上一代传递给下一代。

这些假设构成了Wright-Fisher遗传漂移模型的基础。利用该模型固有的假设，我们可以尝试预测我们可能观察到的中性变异在多代遗传中的模式。Wright-Fisher模型的最后一个规定是，任何一个等位基因被抽中的可能性并不比其他等位基因更大。这就是定义中性的地方——没有正向或负向的选择发生。这看起来可能过于受限，因为我们知道在某些情况下存在适应性差异，但请记住，漂移总是存在，并且影响受选择以及中性变异的等位基因，因此理解漂移至关重要。一种直接计算每代等位基因组成预期变化的方法是主要从概率的角度来考虑遗传。

群体遗传学的二项分布

在讨论概率时，通常假设存在一个潜在的分布，用于描述某个事件发生的可能性或不可能性。在不同的观察结果（分位数）中使用正确的概率分布至关重要。在上一章中，我们使用χ²分布来比较特定类别之间的观察结果。在这里，我们将使用二项分布来处理二元结果的集合。二元事件是指要么发生要么不发生的事件——就像抛硬币一样，要么是正面要么是反面——用这种方式来思考等位基因是非常有用的。 假设我们有一个非常小的种群，由五个二倍体个体组成，它们由两个等位基因构成——一个等位基因以三份拷贝存在（黑色圆圈），另一个以七份拷贝存在（白色圆圈）。如果我们随机抽取圆圈来构成下一代，那么抽取一个黑色等位基因的概率是3/10，抽取一个白色等位基因的概率是7/10。

假设所有拷贝都有相同的繁殖机会，下一代保持相同的大小，即十个拷贝，恰好与之前相同，具有三个黑色等位基因拷贝和七个白色等位基因拷贝的概率是多少？这个结果取决于黑色等位基因被抽样三次，白色等位基因被抽样七次。

在这种情况下，我们可以使用二项分布来计算这种特定结果的概率。二项分布是一种离散概率分布，适用于固定次数的独立实验中成功次数的概率分布，其中每次实验的成功概率相同。在这个例子中，“成功”可以定义为抽取黑色或白色等位基因的事件，而“实验次数”则是总共进行的抽取次数，即十次。

 0.3^3 * 0.7^7

这是一个相当小的概率：大约0.2%。然而，这个方程实际上是不完整的，因为实际上有很多不同的方式可以得到三个黑色和七个白色等位基因的模式。前三个可以是黑色，最后七个是白色，或者第一个、第三个和第五个是黑色，其余是白色，等等。总的组合数可以使用阶乘来计算：

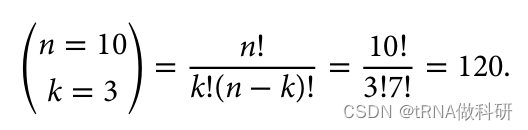
R语言中可以用choose函数进行计算：

 choose(10, 3)

所以下一代中有三个黑色和七个白色等位基因的概率可以计算如下：

120 * 0.3^3 * 0.7^7

这表明，保持从一代到下一代相同比例的几率比我们最初计算的（从0.02%到超过26%）要高得多。 二项概率是指在一系列独立的是/非试验中，获得特定数量成功次数的概率，其中每次试验的成功概率是恒定的。在我们的例子中，每次“试验”相当于从上一代中随机抽取一个等位基因，而“成功”则是指抽取到特定颜色的等位基因。 当我们考虑所有可能的组合时，我们发现下一代保持与上一代相同比例的等位基因的几率实际上远高于最初基于单一序列的计算。这是因为有多种不同的组合方式可以达到相同的比例结果。 这种分析揭示了遗传漂变的一个重要方面：即使在没有选择性压力的情况下，由于随机抽样效应，等位基因频率也可能在世代间发生变化。二项分布提供了一种数学工具，用于量化这种随机变化的预期，并帮助我们理解中性进化理论下遗传变异的动态。 

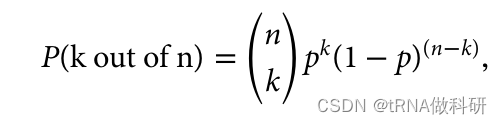
其中n是总样本大小（在我们的例子中是10），k是我们感兴趣的观察到的变异数量（3），p是该类型的频率（0.3）。

因此，在这个小种群中，等位基因频率在下一代保持不变的概率约为四分之一。换句话说，它在下一代发生变化的概率约为四分之三。在统计学中，我们期望当我们取一个样本时，样本中的频率通常与我们从中抽取的原始种群不完全相同。然而，样本越大，我们预期的随机偏差就越小。遗传漂变本质上是进化抽样误差，代际之间的偏差在小种群中（即小样本）更大。 我们也可以很容易地计算出极端情况：下一代将完全由黑色或白色等位基因组成。直觉上我们可以预测，由于频率差异，抽样得到全白色等位基因的概率大于全黑色。下一代获得全白色等位基因的概率是0.7^10 ≈ 0.028。请注意，只有一种方式得到这个结果：所有副本都必须是白色的，所以我们不必担心二项式系数的组合。随机获得全黑色等位基因的概率是0.3^10 ≈ 5.9 × 10^-6。因此，从我们的示例起点来看，我们不期望在一个世代内完全固定或丢失一个等位基因，但更可能的是，由于随机抽样之外没有其他力量，它的频率会发生变化。

二项分布建模

让我们考虑一个二倍体生物体内的单个位点，这里发生了一个突变，使得存在两种可能的等位基因：A和a。我们可以构建一个矩阵，包含仅由这两个等位基因可能产生的所有基因型。记住，我们假设这个生物体是二倍体的，所以我们预期总共会有三种不同的基因型：AA、Aa和aa。 首先，我们要做的是将我们处理的个体数量保存为一个对象（N），然后我们将确定在给定个体数量的情况下，等位基因A的可能拷贝数是多少。可能的拷贝数应该是一个从零（等位基因灭绝）到两倍个体数量的向量（2N），在这个点上，等位基因在种群中固定下来。

N <- 1 #One diploid individual
possible <- 0:(2*N) #Number of possible copies of an allele

我们现在可以绘制二项式概率（P），即在特定的等位基因频率（p）和可能的总体拷贝数（n）下，具有特定拷贝数（k）的概率：

假如我们从A的单拷贝开始计算，那么我们可以计算下一代A拷贝情况的转移矩阵：

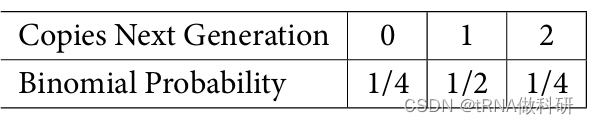
让我们使用R的dbinom函数来获取我们可能的等位基因计数的二项概率，给定所有可能的起始频率。我们将这些二项概率保存为对象P，然后创建一个包含这些值的矩阵，我们将其称为Q：

# 初始化一个向量来存储概率值
P <- NULL

# 对于可能的每个值
for(i in possible){
  # 将二项分布的概率累加到向量P中
  # dbinom函数计算在2*N次试验中，成功次数为'possible'时的概率，
  # 其中每次试验成功的概率为i/(2*N)
  P <- c(P, dbinom(possible, size = 2*N, prob = i/(2*N)))
}

# 将概率向量P转换成一个矩阵，每行有2*N+1个元素
# byrow=TRUE表示按行填充矩阵
Q <- matrix(P, ncol = 2*N+1, byrow = TRUE)

我们有一个转换概率矩阵，它告诉我们从任意起始状态（零个、一个或两个A副本）出发，下一代可能的状态（零个、一个或两个A副本）的概率。矩阵的第一行显示，如果没有A副本，那么下一代保持没有A副本的概率是100%；同理，最后一行显示，如果有两个A副本，那么下一代保持有两个A副本的概率也是100%。这符合我们的模型中的灭绝和固定概念。如果我们假设每一代这些转换概率都成立，那么唯一变化的是起始频率。因此，跨代来看，我们的等位基因A以特定副本数结束的概率是之前每一代转换概率的综合。例如，A在三代后丢失的概率可以这样可视化。

由于我们假设每一代发生的事件与其他任何一代都是独立的，我们可以沿着任何一条路径相乘概率，得到该等位基因遵循这条特定路径的累积概率（概率乘法规则）。因此，A等位基因保持为一个副本然后灭绝的概率就是这两步各自概率的乘积。

如果我们想要计算A等位基因在三代内灭绝的总概率，而不考虑它具体经历了哪条路径，我们需要将所有可能路径的累积概率相加。这是因为每条假设的路径都是互斥的，也就是说，一个等位基因在同一世代内不可能同时经历多于一条路径。

接下来，我们要创建一个矩阵对象，它给我们一个初始状态。为了像我们的转移矩阵那样设置它，我们将让每一列代表我们三个可能的转移状态（零个、一个和两个副本），但在这个矩阵中我们只需要一行。首先，让我们生成一个所有概率都设为零的矩阵对象x，这样我们以后可以轻松地更新它，假设我们从单个A副本开始，这意味着我们将“一个副本”列（第二列）的概率设置为100%：现在，我们可以使用矩阵乘法来获取所有基于我们初始状态的转移概率

x <- matrix(c(rep(0,2*N+1)), ncol=2*N+1, byrow=T)
x[,2] <- 1
(R <- x%*%Q)

while(g[1]<=10){
  (R <- R%*%Q)
  g <- g+1
  points(g, R, col=color, pch=shape)
}

如果你从一个固定的或灭绝的等位基因开始，无论你的循环运行多长时间，它都将保持在这种状态。因此，在这个模型中，固定和灭绝是吸收边界：一旦你变得固定或灭绝，就没有回头路了。

小种群模型模拟

现在，让我们将代码扩展到一些更有趣的内容。让我们考虑一个由十个二倍体个体组成的小种群（因此在种群中总共有二十个位点），同样将从一个个体中出现一个A等位基因开始。

# 设置群体大小为10个二倍体个体
N <- 10

# 可能的等位基因拷贝数从0到2倍的N
possible <- 0:(2*N)

# 初始化概率向量
P <- NULL
# 计算每个可能拷贝数的二项分布概率
for(i in possible){
  P <- c(P, dbinom(possible, size=2*N, prob=i/(2*N)))
}

# 我们的转移矩阵应该是21行乘以21列
Q <- matrix(P, ncol=2*N+1, byrow=TRUE) # 将概率向量P转换为转移矩阵Q

# 创建我们的起始状态矩阵
x <- matrix(c(rep(0,2*N+1)), ncol=2*N+1, byrow=TRUE) # 初始化起始状态矩阵x
x[2] <- 1 # 设置起始时有一个拷贝的概率为100%
R <- x %*% Q # 计算第一代转移概率

# 更改颜色和形状参数，以包括从“灭绝”状态到最终“固定”状态之间的所有条目
color <- c("brown", rep("blue", ncol(R)-2), "grey") # 定义颜色
shape <- c(15, rep(19, ncol(R)-2), 17) # 定义形状

# 从第1代开始所有状态
g <- rep(1, ncol(R)) # 初始化代数向量g
x <- matrix(c(rep(0,2*N+1)), ncol=2*N+1, byrow=TRUE)
x[11] <- 1
x <- as.factor(x)

# 首先创建图形框架
plot(x,xlim=c(1,100), ylim=c(0,1), ylab="Probability", xlab="Generations", type="n")

# 添加图例
legend("bottomleft", legend=c("Extinct", "Intermediate", "Fixed"), col=unique(color), pch=unique(shape), inset=c(0,1), xpd=TRUE, bty="n")

# 循环直到第100代
while(g[1] < 100){
  R <- R %*% Q # 更新转移概率
  g <- g + 1 # 代数加一
  points(g, R, col=color, pch=shape) # 在图中添加点
}

# 最后，让我们在图中添加两条水平线：
abline(h=1/(2*N), lwd=2) # 添加起始等位基因频率A的水平线
abline(h=1-(1/(2*N)), lwd=2, col="orange", lty=2) # 添加起始等位基因频率a的水平线，使用橙色虚线

固定的概率（灰色三角形）似乎正在接近一个渐近线。固定概率似乎增加得非常缓慢，并在5%的概率处趋于平稳。另一方面，灭绝的概率（红色方块）似乎增加得非常快，并在95%处趋于平稳！这有一定的道理：我们说的是每一代都有随机增加或减少频率的机会，如果我们从一个等位基因的拷贝开始，那个等位基因在100代后仍在种群中漂移的概率将会非常小。实际上，这里有一个重要的问题隐藏在显而易见的地方。罕见的等位基因从1/20的频率开始，经过几代后，固定的概率达到了0.05 = 1/20。让我们看看当我们开始改变我们的起始等位基因频率时会发生什么。重新运行我们设置初始拷贝数的代码，这次我们假设一半的个体具有A等位基因（A等位基因频率为50%）

x <- matrix(c(rep(0,2*N+1)), ncol=2*N+1, byrow=T)
x[11] <- 1

灭绝的概率以及固定的概率似乎都有一个更渐进的增加。再次注意，固定概率正好在我们起始等位基因频率50%处趋于平稳，灭绝概率也是如此。在中性遗传漂变下，一个等位基因最终固定的概率等于它在种群中的起始频率。对于全新的突变，这个概率是1/(2N)。

在单个个体的第一种情况中，固定或灭绝的概率在前十代内达到峰值频率，而在更大的种群中，这些概率几乎需要100代才能完全稳定。这表明了种群大小对受遗传漂变影响的等位基因维持的影响。我们将等位基因视为从一个世代抽样以构成下一个世代。遗传漂变是指由于抽样误差导致的等位基因比例的小变化。就像统计抽样误差一样，大样本（大种群）的抽样误差较小；也就是说，每代等位基因频率的总体变化较小。这些变化被称为“中性”的原因在于，观察到的变化显然是随机的，没有方向性。例如，如果一个新突变最终会被固定，那么它大约需要4×N代才能达到固定。此外，在大约N代之后，我们可以假设一个等位基因已经经历了如此多的漂变，以至于它基本上可以处于任何频率（它“忘记”了它的起点）。

下一篇我们将讲解随时间发生的突变。