不相交集类 (并查集)

不相交集类是解决等价问题的一种有效的数据结构，其实现简单，可以使用一个简单的数组，而且每种操作只需要常数时间。

等价关系

称关系(relation) R定义在集合 S 上，如果对于 a, b ∈ S 的每一对元素（a，b），aRb 或者为 true 或者为 false。如果 aRb 是true，那么就说 a 与 b 有关系。

等价关系(equivalence relation)是满足下列3个性质的关系 R：

• （自反性）对于所有的 a ∈ S，aRa。
• （对称性）aRb 当且仅当 bRa。
• （传递性）若 aRb 且 bRc，则 aRc。

例如关系 ≤ 不是等价关系，因为其满足自反性、传递性，但不满足对称性。

动态等价性问题

一个元素 a ∈S 的等价类是 S 的一个子集，它包含所有与 a 有(等价)关系的元素。

解决等价问题的思路：输入数据最初是 N 个集合组成的类，每个集合包含一个元素。初始的表述是所有的关系均为 false（自反的关系除外）。每个集合都有一个不同的元素，从而 S_i ∩ S _j = ∅ 。这使得这些集合不相交(disjoint)。

此时有两种操作允许操作。第一种操作是 find，它返回包含给定元素的集合（即等价类）的名字。第二种操作是添加关系，首先要看是否 a 和 b 已经有关系。这可以通过对 a 和 b 执行 find 并检验它们是否在同一个等价类中来完成。如果不在同一等价类中，则使用求并操作 union。这种操作把含有 a 和 b 的两个等价类合并成一个新的等价类。从集合的角度看，∪ 的结果是建立一个新集合 S_k = S_i∪S_j，去掉原来两个集合，同时保持所有的集合的不相交性。由于这个原因，常常把做这项工作的算法叫作不相交集合的 union/find 算法(disjoint set union/find slgorithm)。

关键：find(a) == find(b) 为 true 当且仅当 a 和 b 在同一个集合中。如果还要跟踪每个等价类的大小，并在执行union时将较小的等价类的名字改为较大的等价类的名字。

基本数据结构

由于只需要父节点的名字，因此可以假设这棵树被非显式地存储在一个数组中：数组的每个成员 s[i] 表示元素 i 的父亲。如果 i 是根，那么 s[i] = -1。

图1 8个元素，初始时在不同的集合中

图2 在union(4, 5)之后

图3 在union(6, 7)之后

图4 在union(4, 6)之后

图5 前面树的隐式表示

灵巧求并算法

按大小求并

上面 union 的实施是相当任意的，它通过使用第二棵树成为第一棵树的子树而完成合并。对其进行简单改进，使得总让较小的树成为较大的树的子树。我们把这种方法叫作按大小求并(union by size)。对于图4，假如下一次运算是union(3, 4)，那么结果将形成图6 所示的森林。倘若没有对大小进行探测而直接union，那么结果将形成更深的树，如图7。

图6 按大小求并的结果

图7 一次任意union 的结果

可以证明，如果这些 union 都是按照大小进行的，那么任何节点的深度均不会超过 logN。

按高度求并

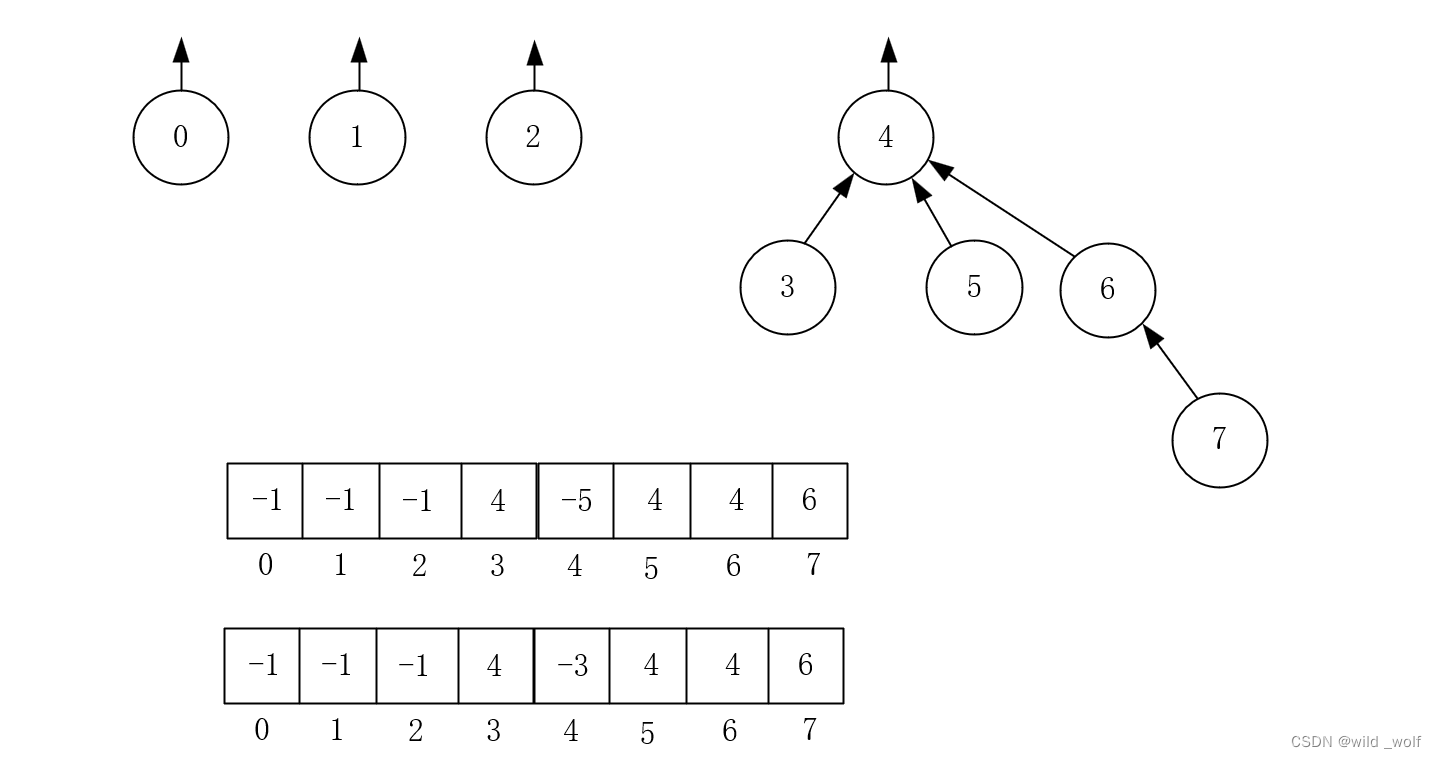
另外一种实现方法为按高度求并(union-by-height)，它同样保证所有的树的深度最多也是 O(logN)。我们跟踪每棵树的高度而不是大小，并执行那些 union 使得浅的树成为深的树的子树。这是一种平缓的算法，因为只有当两棵相等深度的树求并时树的高度才增加（此时树的高度增1）。这样，按高度求并是按大小求并的简单修改。由于零的高度不是负的，因此我们实际上存储高度的负值，减去一个附加的1，并且初始时所有的项都是 -1。

图8 按大小求并和按高度求并隐式表示的森林

/**
* 合并两个不相交集合
* 为简明起见，假设root1和root2是互异的
* 并各代表一个集合的名字
* root1为集合1的根
* root2为集合2的根
*/
void DisjSets::unionSets(int root1, int root2)
{
	if (s[root2] < s[root1]) //root2更深
		s[root1] = root2;	 //使root2为新的根
	else {
		if (s[root1] == s[root2])
			--s[root1];		 //如果相同，则更新高度
		s[root2] = root1;	 //使root1为新的根
	}
}

路径压缩

路径压缩(path compression)在一次 find 操作期间执行而与用来执行 union 的方法无关。设操作为 find(x)，此时路径压缩的效果是，从 x 到根的路径上的每一个节点都使它的父节点变成根。 进行路径压缩时，连续 M 次运算最多需要 O(M logN) 的时间。

/**
* 利用路径压缩执行一次find
* 简单起见，忽略差错检验
* 返回包含x的集合
*/
int DisjSets::find(int x)
{
	if (s[x] < 0)
		return x;
	else
		return s[x] = find(s[x]);
}

实现代码

class DisjSets {
public:
	/**
	* 构造不相交集对象
	* numElements为不相交集的初始个数
	*/
	explicit DisjSets(int numElements):s{ numElements,-1 } {
	}

	/**
	* 执行一次find
	* 为简单起见，再次忽略差错检验
	* 返回包含x的集合
	*/
	int find(int x)const {
		if (s[x] < 0)
			return x;
		else
			return find(s[x]);
	}

	int find(int x) {
		if (s[x] < 0)
			return x;
		else
			return find(s[x]);
	}

	/**
	* 合并两个不相交集合
	* 为简明起见，假设root1和root2是互异的
	* 并各代表一个集合的名字
	* root1为集合1的根
	* root2为集合2的根
	*/
	void unionSets(int root1, int root2)
	{
		s[root2] = root1;
	}

private:
	std::vector<int> s;
};

一个应用

一个应用 union/find 数据结构的例子就是迷宫的生成。