最短路径经典算法--努力学习，更新中qwq

最近更新时间：2021/08/06
前言：

年前学习的最短路径的四个经典算，这里记录这四个算法的粗略思想，以便复习。

1. dijkstra；
2. Bellman-ford；
3. SPFA；
4. floyd ；

稠密图和稀疏图

一个图中，顶点数 n ，边数 m
当 $n^2$ >> m 时,我们称之为稀疏图。
当m相对较大时，我们称之为稠密图。
图的稠密与稀疏是选择最短路算法的一个重要因素，同时也决定了我们建图的方式；

建图选取

当图为稠密图时，使用邻接矩阵来存储图 建图时间复杂度O($n^2$)；
当图为稀疏图时，使用邻接表来储存图 建图时间复杂度为O(m)；

图的建立

这里借用学长的blog.
算法表格：

Dijkstra算法

dijkstra算法是用于解决单源最短路径问题，是非常高效而且稳定的算法。

可用于解决有向图和无向图且边权非负的最短路径问题；

素版dijkstra的时间复杂度为O($m\ast n^2$)；

用小根堆(这里使用STL-priority_queue)优化的dijkstra的时间复杂度($m\ast logn$)；

下面介绍dijkstra的算法思想👇；

算法思想

dijkstra的算法应用了贪心法的思想，即“抄近路走，肯定能找到最短路径”
                              -----------《算法竞赛：入门到进阶》

程序内容

程序的主要内容是维护两个集合S、U。集合S内的元素(结点)是已经确定了最短路径的结点，集合U内的元素是还未求出最短距离的结点(这里的距离是指结点到源点的最短距离)。

算法过程

 1.初始时， S只包含起点s；U包含除s之外的其他顶点，定义：U中顶点的距离为“起点s到该顶点的距离”【例如：U中顶点v的距离为(s, v)的长度，然后若s和v不相邻，则v的距离为∞】。
 2.从U中选出“距离最短的顶点k”(贪心思想)，并将顶点k加入到S中；同时，从U中移除顶点k
 3.更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其他顶点的距离；例如，(s, v)的距离可能大于(s, k)+(k, v)的距离。
 4.重复步骤2和3，直到遍历完所有顶点。

图解算法

文章推荐👆

Dijkstra模板：

// acwing y总模板；
//dijkstra 朴素算法；
//时间复杂度O(m*n^2);
//*稠密图*使用邻接矩阵存图；
//dis[]维护到到起点的最短路径，st[]维护是否在集合S内，n顶点，m 边；
//求s号点到n号点的最短距离，如果不存在，则返回-1
void dijkstra(int s)
{
	memset(dis,inf，sizeof(dis));
	dis[s] = 0;//s为起点
	for(int i = 1; i <= n; i++)
	{
		int k = -1; //在还未确定最短路的点中，寻找距离最小的点
		for(int j = 1; j <= n;j++)
			if(!st[j] && (k == -1 || dis[j] < dis[k]))//st[j] == 0 表明结点j未加入集合S，
				k = j;						//找到集合U内dis最小的结点k后再通过k更新集合U																				
			st[k] = 1;							//内的距离	
		 // 用k更新其他点的距离 
		for(int j = 1; j <= n;j++) dis[j] = min(dis[j],dis[k]+e[k][j]);
		//更新最短路的过程称为松弛操作；
	}
	// 根据题意：
	if (dist[n] == inf) return -1;
    return dist[n];
}

Dijkstra算法的一些问题；

1.dijkstra不能处理负边权的原因：
 由于dijkstra算法采用贪心思想，当结点v加入集合S后一定是到起点的最短路径，即说结点v加入集合S后,dis[v]值不会再发生变化.如果存在负边权，那么就有可能会导致加入集合S后的结点v的dis[v]再次发生改变.例如：

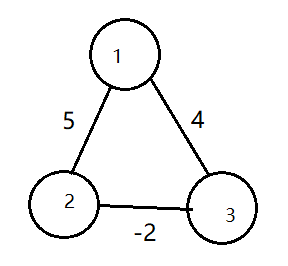
通过程序计算会得出dis[3] = 0，实际上dis[3] = 3，加入集合s的点不再是最短路径，贪心法失效；但是有时存在负边权也能求出正确的结果(思考)，综合来说，dijkstra算法不适用于存在负边权的图；
2.如何理解“松弛”；👈传送门
3.若用重边记得再次更新即：

//重边：
cin >> u >> v >> w;
e[u][v] = e[v][u] = min(w,e[v][u]);

dijkstra算法优化

 我们发现算法过程中的第二步和第三步都可以进行优化，例如 假设当前结点v加入集合S内，然后通过”松弛”操作，更新与它相连的处在集合U的点，并且要排除已经在集合S内的点，（因为已经在集合S内的点的最短路径不会再改变），后把处在集合U更新过的点加入到队列中。
通过第二步可以用logn的复杂度找到“集合U距离最近的点“，代码如下；

// acwing 代码模板
//链式前向星存图
typedef pair<int,int>pll;
int dis[];//维护最短路径
int st[];；//维护集合S true 在集合s内,即该点的最短路径已经求出；
int h[]// 前向星模拟静态链表存前驱
int cnt = 0;
struct node{//存储点的信息
	int to,w,next; 
}edge[];
void add(int u, int v ,int w){
	edge[cnt].to = v;
	edge[cnt].w = w;
	edge[cnt].next = h[u];
	h[u] = cnt++; 
}//前向星存图的加边操作

void dijkstra(int s)
{
	priority_queue<pll,vector<pll>,greater<pll> > q//小根堆语法，背过；
	// first存dis，second存结点编号；
	memset(dis,ox3f,sizeof(dis));
	dis[s] = 0;
	q.push({dis[s],s});//起点入队
	while(!q.empty())//队空结束
	{
		int t = q.top().second;//头元素编号；
		q.pop();//取出并删除头元素，头元素即在集合U内dis最小的值；
		if(st[t]) continue;//若已经加入集合S，dis已经更新完毕，直接跳过；
		st[t] = true;//加入集合S；
		for(int i = h[t];i!=-1;i = edge[i].next)//前向星遍历操作；
		{
			int v = edge[i].to;
			if(dis[v] > dis[t] + edge[i].w)//松弛操作
			{
				dis[v] = dis[t]+edge[i].w;
				//即通过结点t的松弛，使得dis[v]变小，那么更新dis[v];	
				q.push({dis[v],v});
				// 入队
			}
		}
	} 
}

相同思想下的不同代码，体会其中的相同点；

 SPFA

//spfa模板
//前向星建图
void spfa()
{
	memset(dis,0x3f,sizeof(dis));
	dis[s] = 0;
	queue<int>q;
	q.push(s);
	st[s] = 1;
	while(!q.empty())
	{
		int t = q.front();
		q.pop();
		st[t] = 0;
		for(int i = h[t];i != -1; i = e[i].next)
		{
			int v = e[i].to;
			if(dis[v] > dis[t]+e[i].w)
			{
				dis[v] = dis[t]+e[i].w;
				if(!st[v])
				{
					q.push(v);
					st[v] = 1;
				}
			}
		}
	}
	
}

手写双端队列(非原创)：

struct Deque
{
	ll l,r,q[N];
	Deque(){l = r = 0;}
	void empty(){return !(l^r);}
	void push_back(ll v) {q[r++] = v;v%=N;}
	void push_front(ll v) {q[l = (l-1+N)%N] = v;}
	void pop_back() {r = (r-1+N)%N;}
	void pop_front() {l++,l%=N;}
	ll front() {return q[l];}
}

最短路径树

最短路径生成树，就是根节点到达任意点距离最短的路径所构成的树，就是最短路径生成树。
这里取这位大佬图

最短路径树

最小生成树

最小生成树和最短路生成树 相同点在于都是树
在一个图中最短路生成树的个数并不是唯一的，这里我们给出利用乘法原理来进行最短路生成路个数的统计

例题： #10064「一本通 3.1 例 1」黑暗城堡

思路：先用最短路算法求出其余点到顶点①的最短路，然后利用类似prim算法求出每个顶点$i$满足$dis[i]=dis[j]+g[i][j]$ ,j的数量，然后利用乘法原理求出最短路树的个数；
这里乘法原理可以模拟一遍就很清楚成立！
为啥要满足 $dis[i]=dis[j]+g[i][j]$呢？
可知当顶点形成一棵树后就存在父,子结点的关系。

AC code：

/*
    author:@bzdhxs
    date:2021/08/06
    URL:https://loj.ac/p/10064;
    知识点:最短生成树;
*/
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<string>
using namespace std;
#define _orz ios::sync_with_stdio(false),cin.tie(0)
#define mem(str,num) memset(str,num,sizeof(str))
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int mod = 2147483647;
const int N = 3010;
int n,m;
int g[1010][1010];
int dis[N];
int st[N];

void dijkstra(){
    mem(dis,inf);
    dis[1] = 0;
    for(int i = 1; i <= n;i++){
        int cur = -1;
        for(int j = 1; j <= n; j++)
            if(!st[j] && (dis[cur] > dis[j] || cur == -1))
                cur = j;
        st[cur] = 1;

        for(int j = 1; j <= n; j++) dis[j] = min(dis[j],dis[cur]+g[cur][j]);
    }
}


int main()
{
    cin >> n >> m;
    mem(g,inf);
    for(int i = 1; i <= m;i++){
        int u,v,w;
        cin >> u >> v >> w;
        g[u][v] = g[v][u] = min(w,g[v][u]);
    }

    dijkstra();

    //for(int i = 1; i <= n; i++) cout << dis[i] << endl;
    ll res = 1;
    for(int i = 2; i <= n; i++){
        int cnt = 0;
        for(int j = 1; j <= n;j++)
            if(g[i][j] != inf && dis[i] == dis[j]+g[j][i]){
                //cout  << j << "--" << i << endl;
                cnt++;
            }
                
        res = res*cnt %mod;
                
    }
    cout << res << endl;
    return 0;
}