线性代数--高斯消元法

最新推荐文章于 2022-09-24 16:22:12 发布

_Persisting

最新推荐文章于 2022-09-24 16:22:12 发布

阅读量798

点赞数

分类专栏：数据结构+算法学习文章标签：线性代数

本文链接：https://blog.csdn.net/qq_51776588/article/details/121411431

版权

数据结构+算法学习专栏收录该内容

8 篇文章 0 订阅

订阅专栏

模线性方程组

Widget Factory

题目大意：
零件工厂生产若干种零件，生产每种零件都需要花费3~9天的时间。
由于工厂被收购，老员工被开除，新来的员工并不知道生产某种零件需要多长时间。只能依靠之前员工生产零件的记录，来计算零件所需生产时间。
每条记录包含以下信息：
该员工生产的零件总数k、该员工开始在工厂工作的时间、该员工被开除的时间（但是时间仅仅只是记录当天是星期几，无从知晓具体日期）
k个零件的编号也会记录在案
根据所给记录，计算生产各零件所需时间。

思路：
第一想法，设立未知数，求解方程。
对于编号为1~n的零件，设分别需要花费 $x_1,x_2,...,x_3$ 天。
一共给出m条记录，则可以列出m个方程。
关键是对于时间的处理，由于只给出起始时间是星期几，我们并无法算出精确的时间间隔是多少天，但由于生产一个零件最少需3天，最多也只要9天，我们将起始时间看成是同一个星期内的（相当于对7取余），如果算出生产某零件的天数比3天还少，那么直接加7。
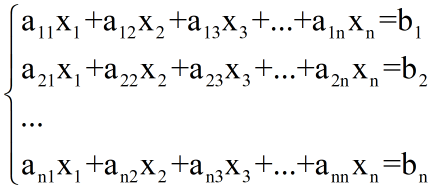
在这里插入图片描述
其中， $a_{ij}$ 表示第i条记录中，第j个零件出现的次数， $b_i$ 表示第i条记录的时间间隔对7取余之后的结果。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#define pb push_back
#define mpi make_pair
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define pi acos(-1)
using namespace std;
typedef long long ll;
const int maxn=1e3+10;
const ll mod=7;
const int INF=0x3f3f3f3f;
typedef pair<int,int> P;
typedef unsigned long long ull;
inline ll lowbit(ll x){return x&(-x);} 
int a[maxn][maxn];
int x[maxn];
bool freeX[maxn];
int GCD(int a,int b){
	return b==0?a:GCD(b,a%b);
}
int LCM(int a,int b){
	return a/GCD(a,b)*b;
}
int get(char s[]){//将星期字符转为具体天
    if(s[0]=='M'&&s[1]=='O'&&s[2]=='N')
        return 1;
    else if(s[0]=='T'&&s[1]=='U'&&s[2]=='E')
        return 2;
    else if(s[0]=='W'&&s[1]=='E'&&s[2]=='D')
        return 3;
    else if(s[0]=='T'&&s[1]=='H'&&s[2]=='U')
        return 4;
    else if(s[0]=='F'&&s[1]=='R'&&s[2]=='I')
        return 5;
    else if(s[0]=='S'&&s[1]=='A'&&s[2]=='T')
        return 6;
    else if(s[0]=='S'&&s[1]=='U'&&s[2]=='N')
        return 7;
}
int Gauss(int equ,int var){
	for(int i=0;i<=var;i++){//初始化 
		x[i]=0;
		freeX[i]=true;
	}
	int col=0;
	int row;
	for(row=0;row<equ&&col<var;row++,col++){
		int maxRow=row;
		for(int i=row+1;i<equ;i++){//寻找当前列的最大值 
			if(abs(a[i][col])>abs(a[maxRow][col])){
				maxRow=i;
			}
		}
		if(maxRow!=row){//交换 
			for(int j=row;j<var+1;j++){
				swap(a[row][j],a[maxRow][j]);
			}
		}
		if(a[row][col]==0){//若寻找当前列最大值，交换之后，当前行当前列仍为0，则说明col列第row行以下全是0，接下来处理当前行的下一列（row不变，col+1） 
			row--;
			continue;
		}
		for(int i=row+1;i<equ;i++){//上三角化 
			if(a[i][col]!=0){
				int lcm=LCM(abs(a[row][col]),abs(a[i][col]));
				int ta=lcm/abs(a[i][col]);
				int tb=lcm/abs(a[row][col]);
				if(a[i][col]*a[row][col]<0) tb*=-1;
				for(int j=col;j<var+1;j++){
					a[i][j]=((a[i][j]*ta-a[row][j]*tb)%mod+mod)%mod;
				}
			}
		}
	} 
	/*求解*/
    //无解：化简的增广阵中存在(0,0,...,a)这样的行，且a!=0
	for(int i=row;i<equ;i++){
		if(a[i][col]!=0){
			return -1;
		}
	}
	//无穷解: 在var*(var+1)的增广阵中出现(0,0,...,0)这样的行
    int temp=var-row;//自由变元有var-row个
    if(row<var){//返回自由变元数
        return temp;
	}
	//唯一解: 在var*(var+1)的增广阵中形成严格的上三角阵
	for(int i=var-1;i>=0;i--){
		int temp=a[i][var];
		for(int j=i+1;j<var;j++){
			if(a[i][j]!=0) temp-=a[i][j]*x[j];
			temp=((temp%mod)+mod)%mod;
		}
		//不断的循环取模判断，直到找出能整除的为止
		while(temp%a[i][i]!=0) temp+=mod;
		x[i]=(temp/a[i][i])%mod;
	}
	return 0;
}
int main(){
	int n,m;
	while(~scanf("%d%d",&n,&m)){
		if(n==0&&m==0) break;
		memset(a,0,sizeof(a));
		for(int i=0;i<m;i++){
			int k;
			char sta[5],end[5];
			scanf("%d %s %s",&k,sta,end);
			a[i][n]=((get(end)-get(sta)+1)%mod+mod)%mod;//计算时间间隔 
			for(int j=0;j<k;j++){
				int type;
				scanf("%d",&type);
				type--;//零件编号改为从0开始
				a[i][type]++;
				a[i][type]%=mod;				
			}
		}
		int free=Gauss(m,n);
		if(free==-1) printf("Inconsistent data.\n");
		else if(free==0){
			for(int i=0;i<n;i++){
				if(x[i]<3) x[i]+=mod;
				printf("%d ",x[i]);
			}    
			printf("\n");
		}
		else printf("Multiple solutions.\n");
	}
	return 0;
}

SETI

主要就是要读懂题目，列出方程组

每条消息可以被转译成一个整数序列 $a_0,a_1,...,a_{n-1}$ ，同时定义函数 $f(k)=\sum_{i=0}^{n-1}a_ik^i(mod)p$ ，且该函数的值始终( $1\leq k\leq n$ )大于等于0，小于等于26。
现在对该函数再次“加密”，用小写字母来表示函数值，a代表1，不代表2，以此类推。用字符’*'来表示0。
对于样例1
31 aaa
表示p=31
$f(1)=a_0\cdot1^0+a_1\cdot1^1+a_2\cdot1^2=1$
$f(2)=a_0\cdot2^0+a_1\cdot2^1+a_2\cdot2^2=1$
$f(3)=a_0\cdot3^0+a_1\cdot3^1+a_2\cdot3^2=1$
很显然，高斯消元求解三元一次方程组，即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#define pb push_back
#define mpi make_pair
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define pi acos(-1)
using namespace std;
typedef long long ll;
const int maxn=1e3+10;
int mod;
const int INF=0x3f3f3f3f;
typedef pair<int,int> P;
typedef unsigned long long ull;
inline ll lowbit(ll x){return x&(-x);} 
int a[maxn][maxn];
int x[maxn];
bool freeX[maxn];
int GCD(int a,int b){
	return b==0?a:GCD(b,a%b);
}
int LCM(int a,int b){
	return a/GCD(a,b)*b;
}
int ksm(int a,int b){
	int ans=1;
	while(b){
		if(b&1) ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return ans;
}
int Gauss(int equ,int var){
	for(int i=0;i<=var;i++){//初始化 
		x[i]=0;
		freeX[i]=true;
	}
	int col=0;
	int row;
	for(row=0;row<equ&&col<var;row++,col++){
		int maxRow=row;
		for(int i=row+1;i<equ;i++){//寻找当前列的最大值 
			if(abs(a[i][col])>abs(a[maxRow][col])){
				maxRow=i;
			}
		}
		if(maxRow!=row){//交换 
			for(int j=row;j<var+1;j++){
				swap(a[row][j],a[maxRow][j]);
			}
		}
		if(a[row][col]==0){//若寻找当前列最大值，交换之后，当前行当前列仍为0，则说明col列第row行以下全是0，接下来处理当前行的下一列（row不变，col+1） 
			row--;
			continue;
		}
		for(int i=row+1;i<equ;i++){//上三角化 
			if(a[i][col]!=0){
				int lcm=LCM(abs(a[row][col]),abs(a[i][col]));
				int ta=lcm/abs(a[i][col]);
				int tb=lcm/abs(a[row][col]);
				if(a[i][col]*a[row][col]<0) tb*=-1;
				for(int j=col;j<var+1;j++){
					a[i][j]=((a[i][j]*ta-a[row][j]*tb)%mod+mod)%mod;
				}
			}
		}
	} 
	/*求解*/
    //无解：化简的增广阵中存在(0,0,...,a)这样的行，且a!=0
	for(int i=row;i<equ;i++){
		if(a[i][col]!=0){
			return -1;
		}
	}
	//无穷解: 在var*(var+1)的增广阵中出现(0,0,...,0)这样的行
    int temp=var-row;//自由变元有var-row个
    if(row<var){//返回自由变元数
        return temp;
	}
	//唯一解: 在var*(var+1)的增广阵中形成严格的上三角阵
	for(int i=var-1;i>=0;i--){
		int temp=a[i][var];
		for(int j=i+1;j<var;j++){
			if(a[i][j]!=0) temp-=a[i][j]*x[j];
			temp=((temp%mod)+mod)%mod;
		}
		//不断的循环取模判断，直到找出能整除的为止
		while(temp%a[i][i]!=0) temp+=mod;
		x[i]=(temp/a[i][i])%mod;
	}
	return 0;
}
int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		char st[100];
		scanf("%d %s",&mod,st);
		int m=strlen(st);
		int n=m;
		for(int i=0;i<m;i++){//构造方程组
			if(st[i]=='*') a[i][n]=0;
			else a[i][n]=st[i]-'a'+1;
			for(int j=0;j<n;j++){
				a[i][j]=ksm(i+1,j)%mod;
			}
		}
		int free=Gauss(m,n);//解方程组
		for(int i=0;i<n;i++){
			printf("%d ",x[i]);
		}
		printf("\n");
	}
	
	return 0;
}

异或方程组

EXTENDED LIGHTS OUT

有一个 $5\times 6$ 的矩形，每个单元格都有两种状态 1、0，改变一个单元格的状态会使得其周围 4 个单元格状态也改变，现在给出每个单元格的状态，要求输出一种能将所有单元格全变为 0 的方案

思路：
将当前状态转变成全0的状态的方案，与将全0状态转换成当前状态的方案相同。
每个单元格仅有0和1两种状态，而且单元格状态的改变和异或运算相同（0^ 1 ^ 1=0)，故使用异或运算。
每改变一个单元格的状态，都会导致整个矩阵状态的改变，因此对于每一个单元格都需要列一个等式，将其状态表示出来。

在这里插入图片描述
其中， $a_{i,j}$ 表示第i个单元格是否受第j个灯的影响，若有影响则赋值为1，否则赋值为0。 $b_i$ 表示第i个单元格的初始状态（输入矩阵）。
解上述异或方程组，解集 ${x_0,x_1,x_2,...,x_{29}\}$ ，即为一种操作方案，它能将当前状态，变为单元格全为0的状态。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int maxn=1e3+10;
const int INF=0x3f3f3f3f;
int a[maxn][maxn];
int x[maxn];
bool freeX[maxn];
int Gauss(int equ,int var){
	for(int i=0;i<=var;i++){//初始化 
		x[i]=0;
		freeX[i]=true;
	}
	int col=0;
	int row;
	for(row=0;row<equ&&col<var;row++,col++){
		int maxRow=row;
		for(int i=row+1;i<equ;i++){//寻找当前列的最大值 
			if(abs(a[i][col])>abs(a[maxRow][col])){
				maxRow=i;
			}
		}
		if(maxRow!=row){//交换 
			for(int j=row;j<var+1;j++){
				swap(a[row][j],a[maxRow][j]);
			}
		}
		if(a[row][col]==0){//若寻找当前列最大值，交换之后，当前行当前列仍为0，则说明col列第row行以下全是0，接下来处理当前行的下一列（row不变，col+1） 
			row--;
			continue;
		}
		for(int i=row+1;i<equ;i++){//上三角化 
			if(a[i][col]!=0){
				for(int j=col;j<var+1;j++){
					a[i][j]^=a[row][j];
				}
			}
		}
	} 
	/*求解*/
	//唯一解: 在var*(var+1)的增广阵中形成严格的上三角阵
	for(int i=var-1;i>=0;i--){
		x[i]=a[i][var];
		for(int j=i+1;j<var;j++){
			x[i]^=(a[i][j]&&x[j]);
		}
	}
	return 0;
}
int dir[][2]={{-1,0},{1,0},{0,-1},{0,1}};
int main(){
	int t;
	scanf("%d",&t);
	for(int tt=1;tt<=t;tt++){
		memset(a,0,sizeof(a));
		for(int i=0;i<5;i++){
			for(int j=0;j<6;j++){//初始化状态矩阵
				int p=i*6+j;
				a[p][p]=1; 
				for(int k=0;k<4;k++){
					int x=i+dir[k][0];
					int y=j+dir[k][1];
					if(x>=0&&x<5&&y>=0&&y<6){
						a[x*6+y][p]=1;
					}
				}
			}
		}
		for(int i=0;i<30;i++){
			scanf("%d",&a[i][30]);
		} 
		Gauss(30,30);
		printf("PUZZLE #%d\n",tt);
		for(int i=0;i<5;i++){
			for(int j=0;j<6;j++){
				printf("%d",x[i*6+j]);
				if(j==5) printf("\n");
				else printf(" ");
			}
		}
	}
	return 0;
}

开关问题

有N个相同的开关，每个开关都与某些开关有着联系，每当你打开或者关闭某个开关的时候，其他的与此开关相关联的开关也会相应地发生变化，即这些相联系的开关的状态如果原来为开就变为关，如果为关就变为开。你的目标是经过若干次开关操作后使得最后N个开关达到一个特定的状态。对于任意一个开关，最多只能进行一次开关操作。你的任务是，计算有多少种可以达到指定状态的方法。（不计开关操作的顺序）
Input
输入第一行有一个数K，表示以下有K组测试数据。
每组测试数据的格式如下：
第一行一个数N（0 < N < 29）
第二行 N个0或者1的数，表示开始时N个开关状态。
第三行 N个0或者1的数，表示操作结束后N个开关的状态。
接下来每行两个数I J，表示如果操作第 I 个开关，第J个开关的状态也会变化。每组数据以 0 0 结束。
Output
如果有可行方法，输出总数，否则输出“Oh,it’s impossible~!!” 不包括引号
Sample Input
2
3
0 0 0
1 1 1
1 2
1 3
2 1
2 3
3 1
3 2
0 0
3
0 0 0
1 0 1
1 2
2 1
0 0
Sample Output
4
Oh,it’s impossible~!!

思路：
与上一题“EXTENDED LIGHTS OUT”的区别在于，从当前状态变为给定状态，而不再是单元格全为0的状态。
但其实是一样的做法，上题中方程组等号右边 $b_i$ 为每个单元格的最终状态，其实是每个单元格当前状态和最终状态的异或值。（任何数和0异或，值不变）
同样的思路，列出方程组，但由于此题并未保证一定有解，因此有三种情况。
1、无解：直接按题目要求输出
2、有解（无穷解/唯一解）：
求出自由元的个数，由于每个自由元都可以取两个状态（0或1），所以方案总数即为 $2^{自由元个数}$
注意：
题目所给“每行两个数I J，表示如果操作第 I 个开关，第J个开关的状态也会变化”，说明第i个开关会影响第j个开关，也就是说第j个开关会受第i个开关的影响，因此赋值时应为： $a [j] [i] = 1$

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int maxn=1e3+10;
int a[maxn][maxn];
int x[maxn];
bool freeX[maxn];
int Gauss(int equ,int var){
	for(int i=0;i<=var;i++){//初始化 
		x[i]=0;
		freeX[i]=true;
	}
	int col=0;//当前处理的列 
	int num=0;//自由元序号 
	int row;
	for(row=0;row<equ&&col<var;row++,col++){
		int maxRow=row;
		for(int i=row+1;i<equ;i++){//寻找当前列的最大值 
			if(abs(a[i][col])>abs(a[maxRow][col])){
				maxRow=i;
			}
		}
		if(maxRow!=row){//交换 
			for(int j=row;j<var+1;j++){
				swap(a[row][j],a[maxRow][j]);
			}
		}
		if(a[row][col]==0){//若寻找当前列最大值，交换之后，当前行当前列仍为0，则说明col列第row行以下全是0，接下来处理当前行的下一列（row不变，col+1） 
			freeX[num++]=col;//记录自由元 
			row--;
			continue;
		}
		for(int i=row+1;i<equ;i++){//上三角化 
			if(a[i][col]!=0){
				for(int j=col;j<var+1;j++){
					a[i][j]^=a[row][j];
				}
			}
		}
	} 
	/*求解*/
	//无解：化简的增广阵中存在(0,0,...,a)这样的行，且a!=0
    for(int i=row;i<equ;i++)
        if(a[i][col]!=0) return -1;
    //无穷解 
    if(var>row) return var-row;
	//唯一解: 在var*(var+1)的增广阵中形成严格的上三角阵
//	for(int i=var-1;i>=0;i--){
//		x[i]=a[i][var];
//		for(int j=i+1;j<var;j++){
//			x[i]^=(a[i][j]&&x[j]);
//		}
//	}
	return 0;
}
int s[maxn],e[maxn];
int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		int n;
		scanf("%d",&n);
		for(int i=0;i<n;i++){
			scanf("%d",&s[i]);
		}
		for(int i=0;i<n;i++){
			scanf("%d",&e[i]);
		}
		memset(a,0,sizeof(a));
		for(int i=0;i<n;i++){
			a[i][n]=s[i]^e[i];
			a[i][i]=1;
		}
		int x,y;
		while(~scanf("%d%d",&x,&y)&&(x+y)){ 
			a[y-1][x-1]=1;
		}	
		int free=Gauss(n,n);
		if(free==-1) puts("Oh,it's impossible~!!");
		else printf("%d\n",1<<free);
	}
	return 0;
}