基于Matlab的音频信号加噪、去噪处理

基于Matlab的音频信号加噪、去噪处理
摘要：当今社会已经进入了高速信息化的时代，用现代科技手段可以更有效的产生、传输、储存和应用语音信号，对于促进信息化发展意义重大。本文利用MATLAB对于所采集的语音信号进行时域、频域分析，模拟加噪环境，设计巴特沃斯滤波器进行滤波，分析滤波前后的语音信号变化和播放对比。
关键词：巴特沃斯滤波器，MATLAB,音频信号
一、研究背景
随着社会发展，人们的生产生活对语音信号质量不断提出更高要求，而语音信号传输过程中不可避免的要受到噪声污染，因此，加强语音信号降噪去噪研究，对改善语音信号质量，提高语音信号清晰度，具有重要的现实意义。本实验旨在对音频文件的采集、调制、滤波，同时对于时域和频域对信号进行相关的分析，获得更多的信息。
二、实验目的
1、学会运用 Matlab 完成对数字滤波器的设计与仿真。 
2、学会使用基本的 Matlab 编程算法
3、深刻理解巴特沃斯滤波器的原理。 
4、学会利用 Matlab 对信号完成采集，取样及快速傅里叶变换。 
5掌握用滤波器对音频信号的进行去噪分析
三、研究内容
1、数字滤波器的概述
2、IIR数字滤波器的理论分析
3、巴特沃斯滤波器的设计
4、对于已知信号的采集及频谱分析
5、学习利用MATLAB的fadtool直接进行滤波器的仿真设计
四、实验分析与仿真结果
1、数字滤波器的概述
  数字滤波器是指输入与输出均为数字信号，通过数值运算处理改变输入信号所含频率成分的相对比例，或者滤出某些频率成分的数字器件或程序。因此是数字滤波器和模拟滤波器知识信号的形式和实现滤波的方法不同。数字滤波器的特点有处理精度高，稳定性好，灵活性强。
2、巴特沃斯滤波器的设计——以低通滤波器为例
（1）概念：巴特沃斯（Butterworth）模拟滤波器是一种典型的模拟滤波器，同
属此类的还有切比雪夫（Chebyshev）滤波器、贝塞尔（Bessel）滤波器等等。巴特沃斯滤波器只需要两个参数表征，滤波器的阶数N和-3dB处的截止频率 。
（2）巴特沃斯低通滤波器设计原理及步骤
步骤如下：
①根据技术指标，求出阶数N
 ； ； 
②求出归一化极点，并得到归一化系统函数。
巴特沃斯低通滤波器的振幅平方函数 
 = 
其中N为滤波器的阶数， 时， =1； ， =1/ , 是3dB截止频率。幅度下降的速度与阶数N有关，N越大，通带越平坦，过渡带越窄，误差越小。
以s换 ，可以将幅度平方函数改写为s的函数

                   
则通过计算可得极点SK和滤波器的表达式： 
对其进行归一化可得到归一化系统函数为 ，其中 ，

只要求出N和截止频率则可以求出系统函数。
③去归一化，得到滤波器系统函数
数字滤波器设计：
①设计经典IIR数字滤波器，首先要设计模拟滤波器
②数字指标要进行归一化，模拟指标也要进行归一化
③数字域和模拟域本征变量映射的关系由脉冲响应不变法或者双线性变换法确定
3、基于巴特沃斯滤波器的音频信号处理仿真实验
(1)对音频文件进行采集
使用matlab中的audioread读入音频信号，在采集的过程中采样频率是由MATLAB软件自行定义的，可知其采样频率为44100Hz，并通过length函数计算得到输入的音频信号的长度N，对音频信号进行快速傅里叶变化，得到原始音频信号的时域和频域波形。

 
图 1原始语音信号频谱图
 
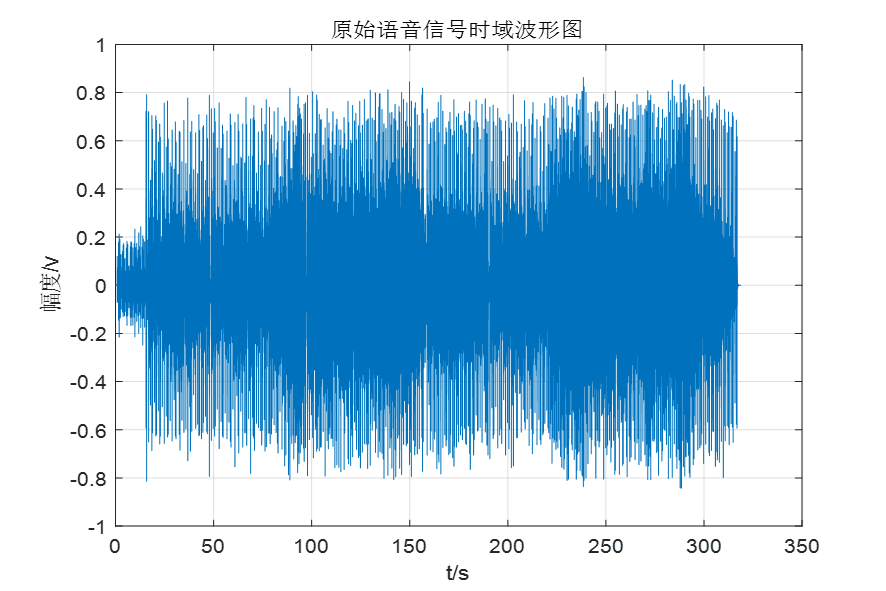
图 2原始语音信号时域图

由于语音信号的频率一般分布在300Hz~3.4kHz，且从原始音频信号频谱图可以看出，该音频信号频率在2000Hz以内。
(2)噪声信号的生成——以余弦噪声信号为例
为了模拟所加噪声，我们设计出幅值为1，频率为5000Hz的余弦波噪声信号。利用matlab绘制其时域波形图和频域图。

 
图 3余弦噪声时域波形图
 
图 4余弦噪声频谱图

从图中可以看出，该余弦信号频率为5000Hz，幅值为1，与设计要求一致。
(3)进行加噪处理
对所给音频信号进行加噪处理，信号与噪声叠加，生成一个新的信号。对加噪后的音频信号进行傅里叶变换，得到信号在频域上的波形，最后绘制时域与频域波形
 
图 5加噪后语音噪声时域图
 
图 6加噪语音信号频谱图
从图中可以看出，音频信号叠加噪声后时域上变得非常密集，频谱中是直接在5000Hz处加入噪声，是线性叠加。此时播放音频信号能明显听到噪声。
(4)设计带阻滤波器
为了滤除所加噪声，我们决定设计一个巴特沃斯带阻滤波器，fp1=4900;fp2=5100;fs1=4990;fs2=5010; 通带最大衰减Rp=1dB; 阻带最小衰减As=30; 并用Matlab计算出滤波器的阶数N=2并绘制该带阻滤波器的幅频特性图。

 
图 7滤波器频谱图

由图可知，滤波器的幅频特性图与所设计一致
(5)低通滤波器的设计
为了滤除所加噪声，我们决定设计一个巴特沃斯低通滤波器，fc=2500HZ，阶数为20，并用Matlab的fdatool仿真出滤波器的模型并绘制该巴特沃斯低通滤波器的幅频特性图。
 
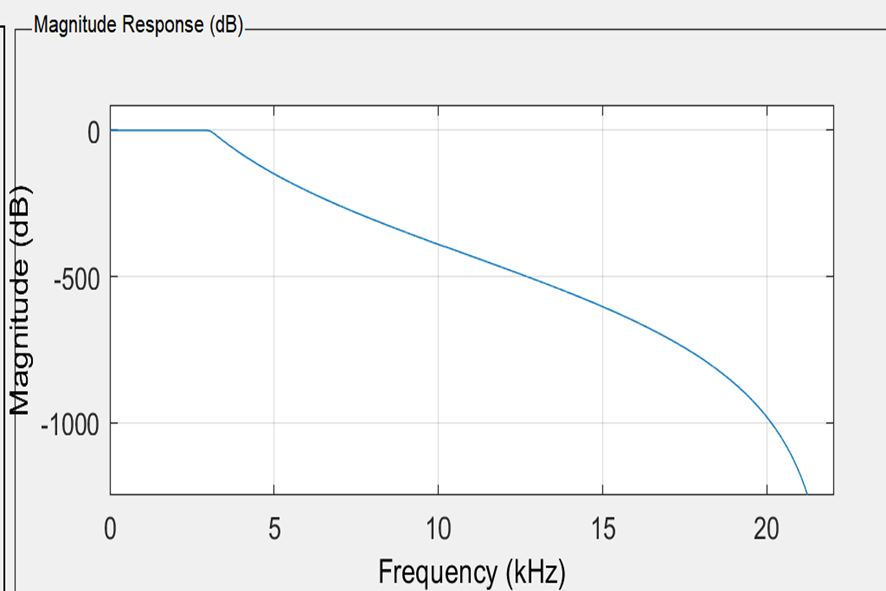
图 8低通滤波器频谱图
 
图 9低通滤波器单位冲激响应图

(6)对于加噪后的噪声进行滤波去噪
音频信号通过带通滤波器后的时域频域图如下：

 
图 10通过带通滤波器频谱图
 
图 11通过带通滤波器后时域图
 
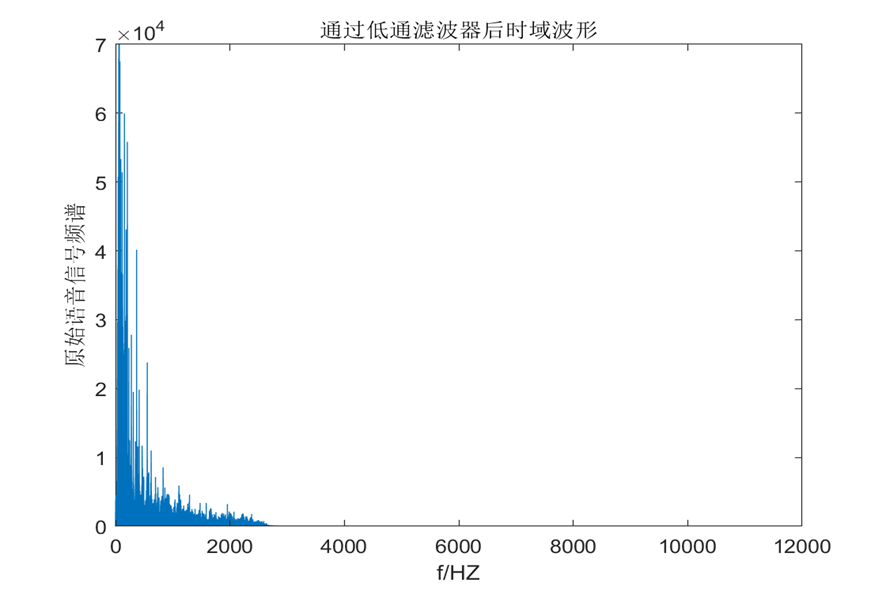
图 12通过低通滤波器频谱图
 
图 13通过低通滤波器时域图
从图中可以看出，音乐信号时域图和频域图都恢复原始波形。播放去噪后的音频已听不出噪声。
五、心得体会
1、在音频信号的加噪去噪实验中，信号的读取以及傅里叶变换分析、确定参数后滤波器的设计以及滤波在matlab中都是比较容易实现的，起初产生余弦噪声是直接使用余弦公式产生，但是对噪声画出的频谱图以及叠加噪声后画出的频谱图并不符合设计要求，最后通过对代码进行分析编译以及查阅相关资料发现是产生余弦噪声的采样率有问题，我们通过对产生余弦噪声的自变量矩阵进行修改使余弦噪声的长度和音频信号的长度相同，最后仿真得到的频谱图与所设计的一致。
2、在本次的实验中加深了我们对于信号采样快速傅里叶变换以及滤波器设计的理解，也学会了如何运用matlab处理语音信号和设计滤波器，提高了我们理论到实践的能力，收获颇多。
六、参考文献
[1]黄波.巴特沃斯数字滤波器的设计与仿真实现[J].河南科技,2021,40(36):10-12.
[2]郗华.基于MATLAB的语音信号处理[J].现代信息科技,2020,4(17):76-78.DOI:10.19850/j.cnki.2096-4706.2020.17.022.
[3]桂成东,谭平平,姜力铭,邓晓婿.基于MATLAB的IIR数字带阻滤波器的设计及研究[J].湖南理工学院学报(自然科学版),2018,31(03):41-46+77.DOI:10.16740/j.cnki.cn43-1421/n.2018.03.009.
七、代码
% clc;clear
[y,fs]=audioread('E:\作业\matlabtest\李荣浩 - 老街.mp3'); %读文件
x=y(:,1)';%双通道变单通道
N=length(x);%计算音频长度
X=fft(x,N); %做傅里叶变换
k=0:N-1;
D=fs/N;%计算频率分辨率
figure;
stem(k*D,abs(X),'Marker','none');
xlabel('f/HZ');
ylabel('幅度/v');
title('原始语音信号频谱');
axis([0,12000,0,70000]);
grid on;
 
t=0:1/fs:1/fs*(N-1);%产生余弦信号的自变量矩阵
figure;
plot(k/fs,x);
xlabel('t/s');
ylabel('幅度/v');
title('原始语音信号时域波形图');
grid on;
 
%绘制噪声信号频谱图
f=5000;
noise=1*cos(2*pi*f*k/fs);
figure;
plot(k/fs,noise);
xlabel('t/s');
ylabel('幅度/v');
title('余弦噪声波形');
axis([0,0.001*pi,-1,1]);
no=fft(noise,N);
figure;
stem(k*D,abs(no),'Marker','none');
xlabel('f/HZ');
ylabel('幅度/v');
title('余弦频谱波形');
xlim([0,6000]);
% noise=noise';
NOISE=x+noise;  
fft_NOISE=fft(NOISE,N);
figure;
plot(k/fs,NOISE);
plot(k/fs,noise);
xlabel('t/s');
ylabel('幅度/v');
title('加噪后时域波形');
 
figure;
stem(k*D,abs(fft_NOISE),'Marker','none');
xlabel('f/HZ');
ylabel('幅度/v');
title('加噪语音信号频谱');
axis([0,12000,0,70000]);
 
%采样频率
fp1=4900;fp2=5100;
fs1=4990;fs2=5010;
wp1=fp1/fs*2*pi;   wp2=fp2/fs*2*pi;   %通带截止频率
wp=[wp1,wp2];
ws1=fs1/fs*2*pi;   ws2=fs2/fs*2*pi;   %阻带截止频率
ws=[ws1,ws2];
Rp=1;As=30;         
[n,wc]=buttord(wp/pi,ws/pi,Rp,As) 
[b,a]=butter(n,wc,'stop') %求数字带阻滤波器系数
[H,w]=freqz(b,a);   
dbH=20*log10(abs(H)/max(abs(H))); 
figure;
plot(w/2/pi*fs,dbH,'r'); 
axis([0,7000,-40,2]);
 
y=filter(b,a,NOISE);
Y=fft(y,N);
figure;
stem(k*D,abs(Y),'Marker','none');
xlabel('f/HZ');
ylabel('原始语音信号频谱');
axis([0,12000,0,70000]);
 
figure;
plot(k/fs,y);
xlabel('t/s');
ylabel('幅度/v');
title('通过带阻滤波器后时域波形');
 %function Hd = ditong
%DITONG Returns a discrete-time filter object.
% MATLAB Code
% Generated by MATLAB(R) 9.6 and Signal Processing Toolbox 8.2.
% Generated on: 16-Dec-2022 16:55:08
% Butterworth Lowpass filter designed using FDESIGN.LOWPASS.
% All frequency values are in Hz.
fs = 44100;  % Sampling Frequency
N  = 20;    % Order
Fc = 2500;  % Cutoff Frequency
% Construct an FDESIGN object and call its BUTTER method.
h  = fdesign.lowpass('N,F3dB', N, Fc, fs);
Hd = design(h, 'butter');
lpf=filter(Hd,NOISE);
LPF=fft(lpf,N);
figure;
stem(k*D,abs(LPF),'Marker','none');
xlabel('f/HZ');
ylabel('原始语音信号频谱');
title('通过低通滤波器后时域波形');
axis([0,12000,0,70000]);
figure;
plot(k/fs,lpf);
xlabel('t/s');
ylabel('幅度/v');
title('通过低通滤波器后时域波形');
%sound(x,fs);
%sound(noise,fs);
%sound(NOISE,fs);
%sound(y,fs);
%sound(lpf,fs);
%clear sound;