化工原理 --- 流体流体 --- 习题课及复习

第一部分 --- 习题课

 

 

1.R1左边那部分空白的高度的计算方法：

在一开始阀门关闭的时候，A和B处的压力是相等的，所以U形管中处处压力相等，液面都是持平的

但是当阀门打开后A和B处的压力就不相等了，此时A处的压力大于B处的压力（伯努利方程），也就是说A会将指示液压下，此时另一边的指示液的高度就会对应上升（在等液面的前提下，下降R1 / 2的话，对面就会上升R1 / 2，此时两液面差就是R1）

中间的U形管中由于充满的是空气，所以压力可以忽略，所以空气两侧的液面的压力相等

 

 

 

1.看到这种涉及到重力的，阻力损失的，百分百要用到伯努利方程（机械能方程），先列一手方程，然后该消的消，消完之后再对计算结果进行分析

1.为什么A截面那只用算R段产生的液柱压强就可以了呢？

这是因为没计算的那段液柱产生的压强和B截面处液柱产生的压强发生了部分重合，直接相互抵消掉了，所以在计算的时候A，B截面的液柱压强都省略掉了这一部分（因为已经被抵消掉了）

---

第二部分 --- 知识点小结

1.在定态流动系统中，任何流体在任意截面处的质量流量都相等

2.在定态流动系统中，不可压缩流体除了在任意截面处的质量流量都相等外，它在任意截面处的体积流量也相等

1.Pe是有效功率

1.上图中公式的左边第一项是剪应力，右边第一项是粘度

1.抛物线分布值的是层流时的速度梯度分布，u是平均流速，umax是最大流速

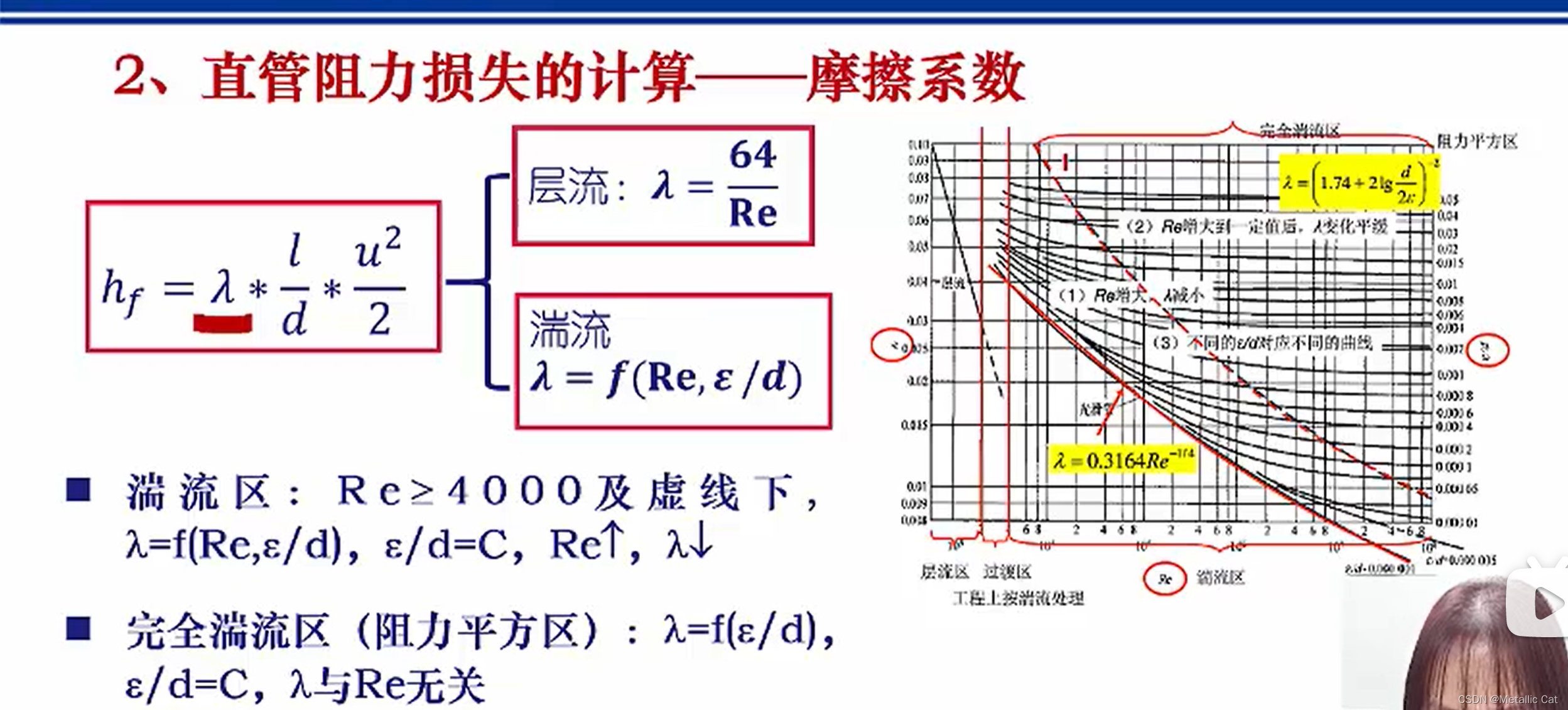
1.Re是雷诺数，nanda是摩擦系数

2.湍流的摩擦系数有两种求法：一种是查图法（两个参数查图，还有一种是公式法）

1.静止的时候流体的流速为0，不需要外界做功，且由于静止也没有阻力损失（阻力损失只有在动起来的时候才会表现出来）

2.结合1的条件以及伯努利方程（机械能方程）我们就能够得到流体的静力学基本方程式 

---

第三部分 --- 选择题

1.注意这一题的条件：流体是流动着的，所以不可以使用静力学基本方程，需要我们使用伯努利方程（机械能方程）来找关系 --- 上图中的公式就是通过伯努利方程找到的关系

当阀门开大的时候，阀门造成的局部阻力就会降低

1.水平管 --- 位能为0，等直径管 --- 连续性方程，速度不变，动能不改变

1.首先列出之前得到的R的通式

2.列出管的伯努利方程，将方程进行变形，使其尽可能的往R的通式靠

3.化简完后将得到的式子代入到R的通式中，代入后就能够得到R表示的是什么物理量的变化了

1.取管道中心为基准面，则两个截面到基准面的垂直距离为0（已经在上面了）

1.两个截面之间的位差指的是两个截面之间的垂直距离

2.流动在阻力平方区意味着流体的摩擦系数nanda和雷诺数没有关系

1.敞口截面具有的特点：表压强为0，流速可近似为无

1.A,C,D都是湍流流动出现阻力损失的原因

2.在层流流动的时候管壁粗糙度不会对阻力损失造成影响

---

第四部分 --- 填空题

注意第二题中的摩擦系数与雷诺数的关系只适用于层流体系

 

1.阀门开度关小，流量减小，流速降低，雷诺数降低，此时摩擦系数增大，但是摩擦系数的变化都很小，增大的量比不上流速减小的量，所以直管阻力hf降低

2.阀门开度关小，阀门的当量长度增大，此时流速的降低比不上阀门当量长度的增大，所以局部阻力hf' 增大

1.那个求和符号的意思是直管阻力 hf 和 局部阻力 hf' 二者求和

1.列直管阻力的方程时候不要忘了雷诺数也与管径和流速有关

2.管径就是管道的内圆的直径

 

1.做这一题的时候不要忘了流速也与管径有关

 

1.阀门关小，流量降低 --- 流量降低，流速降低

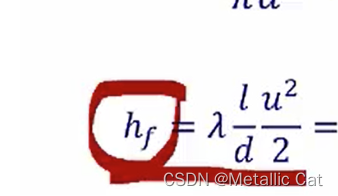
流速降低，直管阻力降低，而在1截面和A截面之间只有直管阻力，且gz1不变，所以压强增大

2.根据连续性方程可知，uA = uB ，所以ub也跟着降低，直管阻力也降低，但是！这些降低带来的总影响都比局部阻力（阀门半关）的增大带来的影响小，而gze1不变，所以压强降低