暑假个人积分赛--21/8/15（A未补）(期望DP个人理解)

暑假个人积分赛–21/8/15

暑假个人积分赛–21/8/15

A

A链接：
题面：
一年一届的比武大赛开始了，老大早姐姐就拉着凡凡来观看比赛，但是凡凡对这种打打杀杀的事情一点也不感兴趣，可是姐姐超爱看，因为姐姐是个花痴，尤其爱那些有腹肌的男人，每次相亲姐姐第一句话就是“你有腹肌吗？”，凡凡想偷偷溜掉，谁知被姐姐发现了，于是姐姐说，想走也可以，但是你得告诉我谁是冠军，不然就老老实实地留在这陪我吧，凡凡是个数学小辣鸡，你能帮凡凡推测出这次大赛的冠军吗？

​ 大赛规则如下：

​ 大赛会给每一个参赛者一个编号，编号从1到n，参赛者各自有一个武力值，武力值高的选手可以击败武力值低的选手，武力值相同擂主获胜。

​ 比赛开始后，选手会按照编号从小到大的顺序依次登上擂台成为擂主进行比武，当出现擂主后，编号比擂主大的选手会按照编号从小到大的顺序去和他PK，胜利者会积一分。

​ 注意：擂主被击败后会立即失去擂主身份,每一个选手都是武林高手，因此他们的恢复能力极强，两个选手PK后，他们的武力值会迅速恢复。

​ 最后积分值最高的选手获胜，当积分值最大的人数大于1个时，输出编号大的。
输入格式：
大赛一共有T场

​ 第一行输入一个数字T (1≤T≤106)

​ 每一场比赛第一行输入一个数字 n (1≤n≤106)，第二行输入各个选手的编号以及他们的武力值 wi (0≤wi≤109)

​ 题目保证：∑n≤106
输出格式：
输出 T 行，每一行输出胜利者的编号以及他的积分。
样例：
input：
2
9
1 7 6 8 9 3 2 4 5
7 18 15 15 11 8 6 17 19
5
5 4 2 1 3
12 12 18 1 5
output：
5 5
2 4

题意分析

题解说的是单调栈的板子题但是我现在还没弄懂咋写…等我晚上来填坑！！！

B

B链接
题面：

题外话：开始比赛的时候看见王宇*很快就过了这一题，我也去看了看这一题，一看这什么鬼，这只知道前面有几个比它小的，怎么确定这个数的值…后来看他们，都把这个题给过了，人都傻了，只有我一个人没见过这个题么，他们怎么都会？？ 原来这题是acwing上的“谜一样的牛”的树状数组板子题，还是我太辣鸡，比赛想了一下树状数组，但是没想到怎么写…

题意：

就是有一个乱序的1~n的全序列，给出n-1个数表示从第二个位置到第n个位置上的数前面有几个数比它小，输出这个序列

思路：

从后往前看来依次确定数字
模拟样例：a[5] = 0 即前面全比它大，那么一定有：ans[5]=剩下数中最小的数即1，剩余：2 3 4 5
a[4] = 1 即前面有一个比它小，那么一定有：ans[4]=剩下数中第二小的数即3，剩余2 4 5
a[3] = 2 即前面有两个比它小，那么一定有：ans[3]=剩下数中第三小的数即5，剩余2 4
a[2] = 1 即前面有一个比它小，那么一定有：ans[2]=剩下数中第二小的数即4，剩余2
a[1] = 0 即前面没有比它小的，那么一定有：ans[1]=剩下数中第一小的数即2
那么序列为：2 4 5 3 1
我们可以用树状数组来维护序列的前缀和，用过的数就是0，没用过的为1，二分来找第i小的数是几

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int tree[N];
int ans[N], a[N];
int n;

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int c)
{
    for(int i = x; i <= n; i += lowbit(i)) tree[i] += c;
}

int sum(int x)
{
    int res = 0;
    for(int i = x; i ; i -= lowbit(i)) res += tree[i];
    
    return res;
}

int main()
{
    scanf("%d", &n);
    for(int i = 2; i <= n; i++) scanf("%d", &a[i]);
    for(int i = 1; i <= n; i++) tree[i] = lowbit(i);
    
    for(int i = n; i >= 1; i --)
    {
        int k = a[i] + 1;
        
        int l = 1, r = n;
        while(l < r)
        {
            int mid = (l + r) / 2;
            if(sum(mid) >= k) r = mid;
            else l = mid + 1;
        }
            
        ans[i] = l;
        add(l, -1);
    }
    
    for(int i = 1; i <= n; i++)
        printf("%d\n", ans[i]);
    
    return 0;
}

F

F链接
题面：

一开始我用的是暴力的dfs,去搜m秒看能到1位置的所有情况，不出意外的T了，其实可以想下，每个人都只可能从他相邻两个方向传过来，那么这不就是dp么！！
状态表示：F[i] [j]:经过 j 秒传到 i 的情况
状态转移方程：F[i] [j] = F[i-1] [j-1] + F[i+1] [j-1]
同时一个人的转态确定之后就不用再搜一遍，直接返回直接用，所以这就是个记忆化的dp(搜索)

//F
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6 + 10;
int f[40][40];
int n, m;

int dfs(int i, int j)
{
	//不为-1，表示已经被更新过了，直接返回值
    if(f[i][j] != -1) return f[i][j];
   
    int last, ne;
    //处理1，n两个位置的特殊情况
    if(i == 1) last = n;
    else last = i - 1;
    if(i == n) ne = 1;
    else ne = i + 1;
    
    f[i][j] = dfs(last, j - 1) + dfs(ne, j - 1);
    
    return f[i][j];
}

int main()
{
    scanf("%d %d", &n, &m);
    
    //-1表示没更新过
    memset(f, -1, sizeof f);
    //在第0秒时：手绢在1号手中，不可能在其他人手中故：
    for(int i = 2; i <= n; i++) f[i][0] = 0;
    f[1][0] = 1;
    //从目标态向下找，一直找到已知态，回溯来更新父节点
    dfs(1, m);
    
    cout << f[1][m] << endl;
    //dsa
    return 0;
}

L

L链接：
题面：

解题思路：

样例遍历顺序：如下图
这个所谓的树的后序遍历就是一个先左后右dfs的过程

//F
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <deque>
#include <stack>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <unordered_map>
#include <string>
#include <vector>
#define PI acos(-1)
#define fi first
#define se second
#define debug freopen("1.in", "r", stdin), freopen("1.out", "w", stdout);
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e5+10, INF = 0x3f3f3f3f;
int n, m;
int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, -1, 1};
int ans[N];
char s[1010];

void dfs(int l, int r)
{
    if(l < r)
    {
        dfs(l, (l+r)/2);
        dfs((l+r)/2+1, r);
    }
    /*
    F -- 0; 
    U -- 1;
    */
    bool F = true, U = true;
    for(int i = l; i <= r; i++)
    {
        if(s[i] == '1') F = false;
        if(s[i] == '0') U = false;
    }
    if(F) printf("F");
    else if(U) printf("U");
    else    printf("O");
    return;
}


int main()
{
	int n;
	scanf("%d", &n);
	scanf("%s", s+1);
	
	dfs(1, 1 << n);
	
	return 0;
}

J

j题链接
题面：
小蝌蚪太可怜了，它又双叒叕找不到妈妈了！
最近青蛙妈妈带小蝌蚪们来到了水上迷宫，青蛙妈妈一再强调“一定要跟紧妈妈”，无奈小蝌蚪太贪玩了，它一会游到这一会游到那，不一会就看不到妈妈了，它很着急，都快哭了，你能帮帮它吗？
迷宫是一个有向无环图，其中包含n个点，m条边，任意两个点互相可达，小蝌蚪游过一条边需要花费一定的时间，
小蝌蚪会从点1出发，妈妈在点n，一个点如果有p条出边，那么小蝌蚪可以随意选择一条路径并且选择每一条路径的概率都是1p，请你帮帮小蝌蚪，算出它找到妈妈一共要游的路径总长期望值。
输入格式：
输入的第一行是两个整数，分别代表图的点数 n 和边数 m。

第 2 到第 m + 1 行，每行有三个整数 u, v, w，代表存在一条从 u 指向 v 长度为 w 的有向边。
输出格式：
输出一行一个实数代表答案，四舍五入保留两位小数。
样例：
input：
4 4
1 2 1
1 3 2
2 3 3
3 4 4
output：
7.00

题意分析：
据说这还是一道板子题…是期望dp的板子题…还是自己太辣鸡，开提高课已经急不可待了

updata:8/19
我是笨比，高中概率统计学了个什么勾八，想了这么长时间才想明白…

首先明白一点：
到达某个结果的期望值 = 这个结果 * 从起始状态到这个状态的概率
什么意思呢？
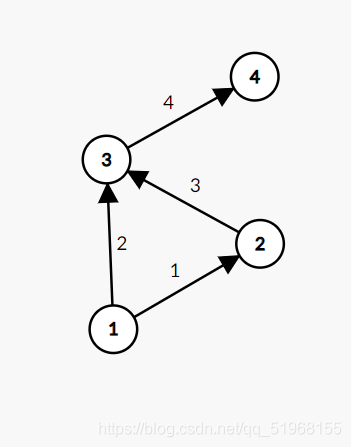
如图：
我们计算从1号点到3号点的期望距离：
$$\begin{gathered} 路径1.1->3:E_1=2\times \frac{1}{2}=1 \\ 路径2.1->2->3:E_2=1\times \frac{1}{2}+3\times \frac{1}{2}=2 \\ 这里路径2中从1到2概率为\frac{1}{2},但单看从2到3概率就是1， \\ 但是从1到3那就是从(1到2的概率)\frac{1}{2}\times 1(2到3的概率)=\frac{1}{2}，总结：概率是要叠乘的 \end{gathered}$$

这题是有正推和倒推两种写法的。
知道上面的东西之后那么我们就可以来搞正推的写法了
正推：
设：a1, a2, a3 … ak 到 j 的权值为 w1, w2, w3 … wk,
从起点到这k个点的概率为：p1, p2, p3 … pk
每个点的出度为：out1, out2, out3, … , outk
注：这里的1~k个点的从起点的到该点的概率一定是确定的也就是说这个点的概率是被更新完的，即此时这个点的入度为0！
那么就有：
$$\begin{gathered} E(i):表示从起点到i点的期望距离 \\ E(J)=\frac{E(a_1)+w_1\times p_1}{ou{t}_1}+\frac{E(a_2)+w_2\times p_2}{ou{t}_2} \\ +\frac{E(a_3)+w_3\times p_3}{ou{t}_3}+...+\frac{E(a_k)+w_k\times p_k}{ou{t}_k} \\ =\sum _{i=1}^k\frac{E(a_i)+w_i\times p_i}{ou{t}_i} \end{gathered}$$

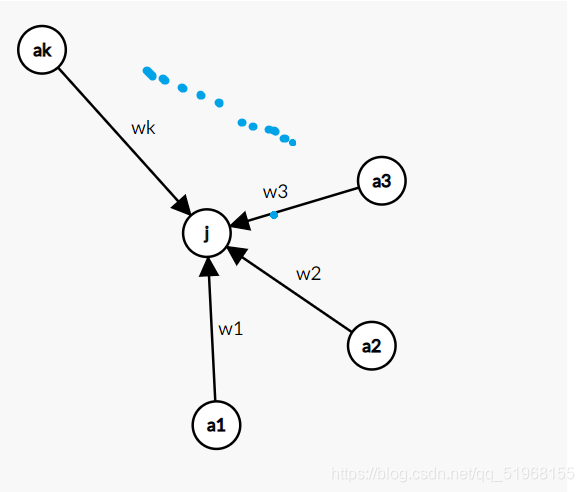
以上即是正推的递推式
代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], w[M], idx;
int n, m;
int out[N], in[N];
double f[N], p[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

double topsort()
{
    queue<int> q;
    for(int i = 1; i <= n; i++)
        if(!in[i]) q.push(i), p[i] = 1;
        
    while(q.size())
    {
        int t = q.front();
        q.pop();
        
        for(int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            f[j] += (w[i] * p[t] + f[t]) * 1.0 / out[t] ;
            p[j] += p[t] * 1.0 / out[t]; 
            in[j]--;
            if(!in[j]) q.push(j);
        }
    }
    
}


int main()
{
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <= n; i++) h[i] = -1;
    while(m--)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
        out[a]++, in[b]++;
    }
    
    topsort();
    // for(int i = 1; i <= n; i++)
    // printf("%d--%.2lf--%.2lf\n", i , f[i], p[i]);
    
    printf("%.2lf", f[n]);
    
    return 0;
}

现在学会了正推，那么咱们来看看逆推，即从终点找到起点
我们令：f(i)表示从i到n的期望距离，那么我们想要的答案即为f(1)
如图：点j通过x1，x2，x3，… , xk到n, 点j到这K个点的距离为：w1, w2, w3 ,… , wk
这K个点到n点的期望距离分别为f1, f2, f3, … , fk
outj:表示j的出度，1/outj:即为j到这K个点的概率
那么我们会有：
$$\begin{gathered} f(j)=\frac{f_1+w_1}{ou{t}_j}+\frac{f_2+w_2}{ou{t}_j}+\frac{f_3+w_3}{ou{t}_j}+...+\frac{f_k+w_k}{ou{t}_j} \\ =\sum _{i=1}^k\frac{f_i+w_i}{ou{t}_j} \end{gathered}$$
根据递推式我们可以看出我们想求f(j)，那我们要求与j相连的点，而求这些相邻的点则要求这些点相邻的点，对你是不是发现，这是个递归回溯的过程，所以我们可以记忆化搜索来解。

关于式子中一个疑惑的解答

$$\begin{gathered} 咱们先看j到x_k的这条路径的柿子：f(j)\stackrel{\text{+}}{=}\frac{f_k+w_k}{ou{t}_j} \\ 这里\frac{w_k}{ou{t}_j}我理解不就是j到x_k的概率乘路径权值嘛， \\ 但是\frac{f_k}{ou{t}_j}这个x_k的期望也要乘j的概率呀？？ \\ 来来来，看这里：咱们一开始就说了，从某个点到某个点的概率是会叠乘的，我们来看看式子中都表示什么含义： \\ f(x_k):仅表示从x_k到n的期望距离，不包含j这个点到x_k这个点概率的影响 \\ f(j):从j到n的期望距离，而在路径上是会经过x_1,x_2,...,x_k这些点的 \\ 所以我们在求f(j)的时候要将j到x_k点概率的影响加到f(x_k)上面即:f(j)\stackrel{\text{+}}{=}\frac{f_k+w_k}{ou{t}_j} \\ 综上：我们使用逆推记忆化搜索的递推式应为： \\ f(j)=((f(能到达状态的期望)+w(能到达状态的权值))\times P(j到能到达状态的概率) \end{gathered}$$

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], w[M], idx;
int n , m;
int dout[N];
double f[N];
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

double dfs(int u)
{
    if(f[u] >= 0) return f[u];
    
    f[u] = 0;
    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        f[u] += (dfs(j) + w[i])/ dout[u];
    }
    
    return f[u];
}

int main()
{
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <= n; i++) h[i] = -1, f[i] = -1;
    
    int a, b, c;
    for(int i = 1; i <= m; i++)
    {
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
        dout[a] ++;
    }
    
    f[n] = 0;
    dfs(1);
    
    printf("%.2lf", f[1]);
    
    return 0;
}