无线系统笔记（2）----麦克斯韦方程组

和田龙二

已于 2022-03-09 10:04:28 修改

阅读量1.2k

点赞数 2

文章标签：学习

于 2022-03-07 17:50:30 首次发布

本文链接：https://blog.csdn.net/qq_52201307/article/details/123333559

版权

概念简述--电场强度和电通量

电场强度

1. 多个点电荷产生的电场在某一点的电场强度

概念简述--电场强度和电通量

电场强度

1. 多个点电荷产生的电场在某一点的电场强度

现在存在如图所示的电场，试求图中四个点电荷对图中点的电场强度，只需单独求每个点电荷的强度再相加即可，即如下公式：

$\LARGE{}E (P)=\frac{1}{4 \pi \epsilon_0}\sum _{i} \frac{Q_{i}}{r_{i}^2} \hat{\boldsymbol{r_{_{i}}}}$

1. 不规则形状的电场在某一点的电场强度

对不规则的电场，同样可以将其视为多个点电荷的叠加，电场强度只需用积分求出即可，公式如下

$\LARGE\mathbf{E} = \int_V d\mathbf{E} = \frac{1}{4\pi\varepsilon_0} \int_V\frac{\rho}{r^2} \mathbf{\hat{r}}\,\mathrm{d}V = \frac{1}{4\pi\varepsilon_0} \int_V\frac{\rho}{r^3} \mathbf{r}\,\mathrm{d}V \,\!$

电通量

如前文所示，电荷的周围充斥着电场，电场可以由向外辐射的射线表示，称为电场线

可以粗略的认为通过某一个特定面积的电场线条数越多，这一面积的电通量就越大

斯托克斯定理

对于任意矢量F， $\int _{\mathbb {S} }\nabla \times \mathbf {F} \cdot \mathrm {d} \mathbf {a} =\oint _{\mathbb {C} }\mathbf {F} \cdot \mathrm {d} {\boldsymbol {\ell }}$ 。

因此，下文中出现的麦克斯韦方程组都具有积分和微分两种形式

正题----麦克斯韦方程组

麦克斯韦方程组清楚地描述了电场和磁场的特性以及他们之间的关系

其中共包含四个方程：

1. 电场的高斯定律

2. 磁场的高斯定律

3. 法拉第定律（变化的磁场产生电场）

4. 安培麦克斯韦方程（变化的磁场产生电场）

重提电场强度的计算

在前文中已经提到过电场强度计算的基本方法，这里再提出一些上述方法的运用案例

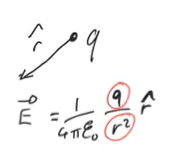
对于点电荷，按照公式计算即可

对具有固定电荷量的点状电场，按照叠加原理计算即可

对于长直导线，其周围具有圆形电场，对其圆形面积内的电荷叠加求场强即可

对于矩形平面，求面积再积分即可（后两个要再问

磁场大小的计算

与电场类似，磁场强度大小也可以用类似的方法计算

长直导线周围磁场大小：

环形导线磁场大小：

螺旋线圈磁场大小：

麦克斯韦方程组

接下来介绍麦克斯韦方程组，每个方程不仅有一个积分形式，也有一个偏微分形式

1. 电场的高斯定律

内容（截取wiki）：穿越出任意闭合曲面的净电通量等于该闭合曲面内的净电荷除以电容率。该闭合曲面称为高斯曲面

“da”是闭合曲面的面积，q是曲面电荷量

微分形式： $\nabla \cdot \mathbf{E} =\frac{\rho}{\epsilon_0}$ $\rho$ 为电荷密度

下图为微分形式示意图，可以理解为某个点不同电场强度的总作用

2. 磁场的高斯定律

定义：一个固定磁场的散度为0，也就是说，磁极的正负是成对出现的，不存在磁单极子

积分形式：

$\oiint{\displaystyle \scriptstyle S}\scriptstyle S {\displaystyle \mathbf {B} \cdot \mathrm {d} \mathbf {S} =0}{\displaystyle \mathbf {B} \cdot \mathrm {d} \mathbf {S} =0}$

微分形式：

$\nabla \cdot {\mathbf {B}}=0$

3. 法拉第感应定律

用来定量表示变化的磁场产生电场

积分形式：（截取自wiki）

$\oint _{{\partial \Sigma }}{\mathbf {E}}\cdot d{\boldsymbol {\ell }}=-\ \iint _{{\Sigma }}{\partial \over {\partial t}}{\mathbf {B}}\cdot d{\mathbf {A}} {\displaystyle =-\ {\partial \over {\partial t}}\iint _{\Sigma }\mathbf {B} \cdot d\mathbf {A} }=-\ {\partial \over {\partial t}}\iint _{{\Sigma }}{\mathbf {B}}\cdot d{\mathbf {A}}$

Σ为一被闭合围道∂Σ包围的曲面；Σ与∂Σ皆为固定的，不随时间变动；

E为电场；

dℓ为围道∂Σ的一无限小矢量元；

B为磁场；

dA为曲面Σ的一无限小矢量元，其大小相等于一块无限小曲面，而其方向与该块曲面成正交。

微分形式：

$\nabla \times {\mathbf {E}}({\mathbf {r}},\ t)=-{\frac {\partial {\mathbf {B}}({\mathbf {r}},\ t)}{\partial t}}$

$\nabla$ x代表旋度；

E为电场；

B为磁场。

图片表示：

简单来说就是固定平面磁通量的改变会产生电场

4. 麦克斯韦-安培定律

和3相反，这里是描述电场如何产生磁场

原版安培定律描绘了真空载流导线和闭合回路磁场之间的关系。公式为：

$\oint _{\mathbb {C} }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I_{\text{enc}}$

$\nabla \times {\mathbf {B}}=\mu _{0}{\mathbf {J}}$

然而，该公式仅在静磁学环境下适用。当引入时间维度时会无效。因为对微分公式求散度可得

$\nabla \cdot (\nabla \times {\mathbf {B}})=\mu _{0}\nabla \cdot {\mathbf {J}}$

根据相关运算规则可知旋度的散度恒等于0，因此电流密度的散度等于0

选取一正在充电的电容器，由于电流为0，因此选择不同曲面进行积分得到的结果不同，这是不被允许的

麦克斯韦修正的版本：

$\nabla \times {\mathbf {B}}=\mu _{0}{\mathbf {J}}+\mu _{0}\varepsilon _{0}{\frac {\partial {\mathbf {E}}}{\partial t}}$

$\nabla \times {\mathbf {H}}={\mathbf {J}}_{f}+{\frac {\partial {\mathbf {D}}}{\partial t}}$

仔细地观察麦克斯韦方程组，就可以发现这方程组很明确地解释了电磁波怎样传播于空间。根据法拉第感应定律，时变磁场会生成电场；根据麦克斯韦-安培定律，时变电场又生成了磁场。这不停的循环使得电磁波能够以光速传播于空间。（截取自WIKI）

和田龙二

关注

2
点赞
踩
6

收藏

觉得还不错? 一键收藏
0
评论
无线系统笔记（2）----麦克斯韦方程组

概念简述--电场强度和电通量电场强度1. 多个点电荷产生的电场在某一点的电场强度现在存在如图所示的电场，试求图中四个点电荷对图中点的电场强度，只需单独求每个点电荷的强度再相加即可，即如下公式：1. 不规则形状的电场在某一点的电场强度对不规则的电场，同样可以将其视为多个点电荷的叠加，电场强度只需用积分求出即可，公式如下电通量如前文所示，电荷的周围充斥着电场，电场可以由...
复制链接

扫一扫