机器学习——SVM

最新推荐文章于 2023-12-27 15:11:45 发布
最新推荐文章于 2023-12-27 15:11:45 发布
阅读量1.8k 收藏 3
点赞数 1
文章标签： 机器学习 sklearn python
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_52383774/article/details/119949126
版权

本文章是学习笔记，内容可能会有很多漏洞，如果有不正确的地方欢迎指正
**

一、SVM简述

   1、概念
   在机器学习领域，支持向量机SVM(Support Vector Machine)是一个有监督的学习模 型，通常用来进行模式识别、分类(异常值检测)以及回归分析。

SVM可分为3种。
（1）数据线性可分：硬件隔SVM
（2）数据近似线性可分：软间隔SVM
（3）数据不可线性分：核技巧

二、硬间隔优化问题导出（Hard Margin）

   1、线性模型
      通过对决策边界的平移来决定，保证决策边界在两个刚刚碰到数据集的的中间位置
在这里插入图片描述      1.1、决策边界
         数据集处于不同的位置，在决策边界的上方或者是下方，可分别归为+1类和-1类
在这里插入图片描述   2、线性可分SVM——硬件隔SVM
      2.1、优化问题的导出
         2.1.1、二维空间
在这里插入图片描述         2.1.2、三维空间
在这里插入图片描述         2.1.3、高维空间：超平面
         2.1.4、最大化d（间隔）
在这里插入图片描述直线2： ω x + b = 0 \omega x+b=0 ωx+b=0，而直线1、3都是由直线2平移过来的。

直线1： ω x + b = k \omega x+b=k ωx+b=k 直线3： ω x + b = − k \omega x+b=-k ωx+b=−k

对于两边都除以k，就得到 ω k x + b k = 1 \frac{\omega }{k}x+\frac{b}{k}=1 kω​x+kb​=1 和 ω k x + b k = − 1 \frac{\omega }{k}x+\frac{b}{k}=-1 kω​x+kb​=−1

对于直线2，两边都乘上 1 k \frac{1}{k} k1​ 得到 ω k x + b k = 0 \frac{\omega }{k}x+\frac{b}{k}=0 kω​x+kb​=0
在这里插入图片描述这时我们可以得到三个全新的式子。

直线1： ω x + b = 1 \omega x+b=1 ωx+b=1

直线2： ω x + b = − 1 \omega x+b=-1 ωx+b=−1

直线3： ω x + b = 0 \omega x+b=0 ωx+b=0
注意：这里的 ω \omega ω 和 b b b 的与上文中的不相同，这里的是更新过后的 ω \omega ω 和 b b b

上文说过，这里的 x ， ω x，\omega x，ω是向量，所以 x 1 − x 2 x_1-x_2 x1​−x2​ 得到的是 x 2 x 1 x_2x_1 x2​x1​ 的那一段向量
之后是向量相乘，注意上面的 c o s θ cos\theta cosθ 可以由公式表示出d，与 ω \omega ω 建立关系 d = 2 ∣ ∣ ω ∣ ∣ d=\frac{2}{||\omega||} d=∣∣ω∣∣2​。
m a x max max d 不就是 m i n min min 1 2 ∣ ∣ ω ∣ ∣ 2 \frac{1}{2}||\omega||^2 21​∣∣ω∣∣2 （ ∣ ∣ ω ∣ ∣ ||\omega|| ∣∣ω∣∣表示为模长，在这个式子中是有根号的，所以这里需要平方一下，以便更好的计算）

问题的转化：最大化间隔 d ⇒ \Rightarrow ⇒ 最小化 1 2 ∣ ∣ ω ∣ ∣ 2 \frac{1}{2}||\omega||^2 21​∣∣ω∣∣2

在这里插入图片描述分析约束条件，发现不论数据集的分布在直线1上还是直线3下，都成立以下的式子
在这里插入图片描述我们得到SVM优化问题：在这里插入图片描述
   3、例子

ω \omega ω 是法向量，这里设定的是二维平面，所以 ω \omega ω 有两个参数，就有了（ ω 1 \omega_1 ω1​ 和 ω 2 \omega_2 ω2​）
在这里插入图片描述在这里插入图片描述
在这里插入图片描述接下来进行化简，改变了约束条件
在这里插入图片描述最后解出 ω 1 \omega_1 ω1​ 和 ω 2 \omega_2 ω2​ 和 b
在这里插入图片描述   4、优化问题求解
      4.1、拉格朗日数乘法**
            拉氏乘数法主要用来求解带约束条件下的极值

            例子
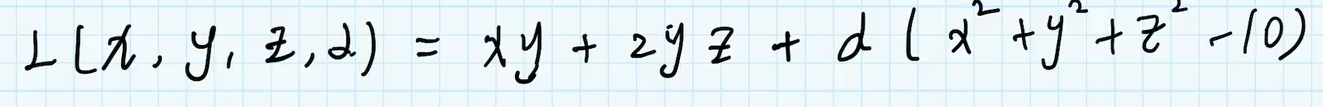
在这里插入图片描述             （1）构造拉氏函数
在这里插入图片描述
             （2）分别求导数
在这里插入图片描述在这里插入图片描述             （3）总结拉氏函数
                 注意：在给出的约束条件中，s.t 有几个约束，就可以有几个参数（系数）
在这里插入图片描述             （4）SVM优化问题的拉氏函数
                 因为 x , ω x,\omega x,ω都是向量，所以有许多的约束条件，在这里我们将其写成连加的形式。
在这里插入图片描述

      4.2、原问题与拉格朗对偶问题
            4.2.1、原问题
在这里插入图片描述在这里插入图片描述            4.2.2、对偶问题

                     先对拉氏函数求最小值，对参数 ω \omega ω求最小值（表示下确界的意思，就是无限的接近，有可能取的到，有可能取不到），在对拉氏函数求最大值（对 α , β \alpha,\beta α,β求最大值）

            4.2.3、KKT条件
             （1）定理1
                如果 ω \omega ω 是原问题的最优解，而 α , β \alpha,\beta α,β 是对偶问题的最优解。 那么就有 f ( ω ) ≥ θ ( α , β ) f(\omega) \geq \theta(\alpha,\beta) f(ω)≥θ(α,β)
                证明
                  先最小化原问题的最优解（意味着，随便带入一个 ω \omega ω 都比他大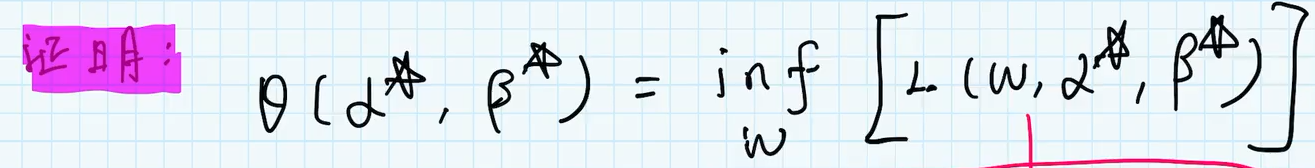）在这里插入图片描述根据上文提到 h ( ω ) = 0 h(\omega)=0 h(ω)=0 和 g ( ω ) ⩽ 0 g(\omega)\leqslant0 g(ω)⩽0的条件，得到

在这里插入图片描述             （2）定理2：原问题与对偶问题之间的间距
在这里插入图片描述             （3）强对偶定理

在这里插入图片描述拉氏函数的最小值，随便带入一个值都比它大
在这里插入图片描述在这里插入图片描述

三、参考

https://www.bilibili.com/video/BV1A4411y7qK?from=search&seid=11601349198549504545

本文章还未更新完毕未来会继续更新

白某啥也不会
关注
  • 1
    点赞
  • 踩
  • 3
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
【全解】基于OpenCv的SVM实现车牌检测与识别
cv君的博客
05-13 4万+
都说深度学习的出现极力地打压着传统机器学习算法的地位，作为一个二刷机器学习经典算法的小伙伴告诉你：还真多半是这样，咳，毕竟还是差距较大，深度学习处理真实世界多维度的问题更权威！不过，有的事情还是机器学习能做的，经典永不过时，下面我们来做一个实践。 前两篇博客比较仓促，今天我把全部整理了一遍，流程图过程也全部展现，让大家更好的明白流程 ，篇幅字数上万，建议细品！ 我们来看看车牌检测基本的识别流程： 我使用的是OpenCv自带的SVM模型，由于SVM的突出表现，得到了更多官方的青睐，就诞生出了很多方便使用的.
svm.rar_SVM模式识别_svm识别分类
09-20
本程序实现了用SVM进行模式识别分类，里面带有实例 非常有用
支持向量机SVM
Allmyg的博客
08-26 1179
SVM是什么 SVM（全称Support Vector Machine）中文名称支持向量机。SVM是一种二分类算法，所谓二分类即把具有多个特性（属性）的数据分为两类。它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。 线性分类 如果需要分类的数据都是线性可分的，那么只需要一根直线f(x)=wx+b就可以分开了，如下图所示，现在有一个二维平面，平面上有两种不同的数据，分别用圈和叉表示。由于这些数据是线性可分的，所以可以用一条
SVM详细讲解
张迁的博客
03-05 8298
1. 目标      SVM是一个二类分类器，它的目标是找到一个超平面，使用两类数据离超平面越远越好，从而对新的数据分类更准确，即使分类器更加健壮。      支持向量（Support Vetor）：就是离分隔超平面最近...
基于支持向量机（SVM）的人脸识别
热门推荐
Dania的思考与记录
05-06 3万+
下定决心开始写博客，希望能在写博客的过程中，总结思路，加深理解。在这里分享心得体会，共同进步。如有不足之处望批评指正。本博客包含本人学习SVM和PCA的笔记，简要的说明其原理和方法步奏，人脸识别程序的解释说明，一并奉上完整的Matlab代码和相关的学习资料。感觉自己在这上面花了不少时间但停留在一个较浅层次的了解上，希望后面学习SVM的朋友们能少走弯路。本人才疏学浅，博客难免有错漏，请见谅。如有转载请
SVM模型详解
tt丫的博客
04-01 2万+
入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。 一、SVM定义与解决目标 SVM是一个二类分类器。其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化成一个凸二次规划问题的求解。即找到一个超平面，使两类数据离超平面越远越好，这样就可以让模型对新的数据分类更准确，即分类器更加稳定。 🎈支持向量：离分隔超平面最近的一些点 🎈间隔最大化：寻找最大化支持向量到分隔超平面的距离，以此为目标来求出分隔超平面 🎈数据分类
机器学习之SVM
湫兮如风i的博客
10-20 4365
机器学习之SVM
SVM优缺点
XKira的专栏
06-04 8713
优点： 对高维空间适应良好； 即使在数据维度数比样本数多的情况下也表现良好； 只需训练集的一个子集（支持向量），因此很节约内存； 根据不同的目标可以使用不同的核函数，除了已提供的常用核函数，scikit-learn也支持自定义核函数。 缺点： 如果数据的特征数比样本数要多很多，则SVM的表现很差； SVM并不直接提供定量的可能性预计，这些通常通过代价高昂的交叉验证法实现。
svm.svm_什么是svm
weixin_26640663的博客
09-16 271
svm.svmSupport Vector Machine (SVM) is an approach for classification which uses the concept of separating hyperplane. It was developed in the 1990s. It is a generalization of an intuitive and simple ...
机器学习—SVM
cy925777075的博客
08-14 1336
支持向量机（SVM） 如果没学过SVM的话那就等于没有学过机器学习。SVM作为机器学习中最经典的算法之一在2012年之前曾叱咤风云，可以说除了集成算法或深度学习之外是一个最好的分类器。 SVM的类型有三种，即线性可分支持向量机、软间隔支持向量机以及非线性支持向量机。由于本文是对算法进行概括，因此手推支持向量机的任务这里就不描述了，感兴趣的话大家可以自己拿笔在纸上划拉划拉~~！ 线性可分支持向量机（硬间隔支持向量机），即样本数据是线性可分的，如图所示。 换句话说SVM总能找到一个超平面是距离超平面最近的样本
机器学习——SVM，微博不实信息分类
06-24
利用支持向量机对于微博爬取的不实信息进行分类，并且爬取正常的微博信息，判断微博是否不实。其中正常微博为0，不实微博为1
机器学习——SVM向量支持机
05-22
机器学习支持向灵机数学模型，包含上课时用的PDF以及PPT文档
OpenCV机器学习——支持向量机SVM
01-27
OpenCV中集成了多种机器学习算法供我们方便使用，如果我们要训练数据进行分类，不用自己写分类器，只需要调用相应的库和类即可轻松实现。本文重点不在于介绍机器学习原理及数学推导，着重介绍OpenCV中的机器学习相关...
机器学习——支持向量机SVM算法完整实战源码
05-16
基于Python和sklearn机器学习库实现的支持向量机算法使用的实战案例。 使用jupyter notebook环境开发。 支持向量机：支持向量机（Support Vector Machine, SVM）是一类按监督学习（supervised learning）方式对数据...
实验报告——SVM手写数字识别实现
01-22
实验报告——SVM手写数字识别实现
【应用篇】支持向量机SVM识别数字集（数据采集+模型训练+预测输出）
拨雪寻春，烧灯续昼
03-30 5728
使用SVM和OPNECV做了简单的数字识别和采集，电赛可用版
模式识别与机器学习-SVM（线性支持向量机）
最新发布
Kilig___的博客
12-27 834
谨以此博客作为复习期间的记录。
支持向量机（SVM）
星辰的博客
01-17 2万+
算法简介 支持向量机(SVM)是种二类分类模型。 它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机:支持向量机还包括核技巧，这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。 支持向量机学习方法包含构建由简至繁的模型:线性可分支持向量机、线性支持向量机以及非线性支持向量机。简单模型是复杂模型的基础，也是复杂模型的特殊情况。当训练数据线
SVM支持向量机原理详解
LinxRds的博客
10-20 1307
SVM 考虑一个二分类问题。假设输入空间与特征空间为两个不同的空间。输入空间为欧式空间或离散集合，特征空间为欧式空间或希尔伯特空间。线性可分支持向量机、线性支持向量机假设这两个空间的元素一一对应，并将输入空间中的输入映射为特征空间中的特征向量。非线性支持向量机利用一个从输入空间到特征空间的非线性映射将输入映射为特征向量。所以，输入都由输入空间转换到特征空间，支持向量机的学习是在特征空间进行的。 希尔伯特空间：一个完备的内积空间。其中的元素可以度量长度以及元素之间的角度。相比于欧式空间的基底常为正交的实数轴
Sklearn 损失函数如何应用到_Python机器学习笔记：SVM（4）——sklearn实现
05-31
Sklearn中的损失函数是通过模型的loss参数来设置的。在SVM中，常用的损失函数有hinge损失和squared_hinge损失。 hinge损失函数是一种基于最大间隔的分类器损失函数，常用于线性SVM中。它的数学表达式为： $$\max(0, 1 - y_i(w \cdot x_i + b))$$ 其中，$y_i$表示第$i$个样本的真实标签，$w$和$b$表示线性SVM的参数，$x_i$表示第$i$个样本的特征。 squared_hinge损失函数是hinge损失函数的平方，它的数学表达式为： $$\max(0, 1 - y_i(w \cdot x_i + b))^2$$ 在Sklearn中，我们可以通过设置SVC类的loss参数来选择使用哪种损失函数。默认情况下，Sklearn使用hinge损失函数，即loss='hinge'。如果想使用squared_hinge损失函数，我们可以将loss参数设置为'squared_hinge'。例如： ```python from sklearn.svm import SVC # 使用hinge损失函数的线性SVM linear_svm = SVC(kernel='linear', C=1.0, loss='hinge') # 使用squared_hinge损失函数的线性SVM linear_svm = SVC(kernel='linear', C=1.0, loss='squared_hinge') ```

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值