数学建模笔记（五）：简单优化模型

原创 已于 2022-07-12 11:01:44 修改 · 6.7k 阅读 · 142 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#优化模型 #数学建模

于 2022-07-02 17:42:36 首次发布
本文精选多个数学模型案例，包括存贮模型、森林救火、倾倒的啤酒杯等问题的分析与解决过程。每个案例均详细介绍了问题背景、模型假设、模型建立及求解方法等内容。

文章目录

前言

在这里插入图片描述

一 、存贮模型

1.问题背景（不允许缺货）

在这里插入图片描述

2.问题分析

由周期长度所决定日均费用
在这里插入图片描述
在这里插入图片描述

3.模型假设

先不做拓展，从最简单的情况出发，后续可以讨论生产时间（每日生产个数上限），需求量变化。
在这里插入图片描述

4.模型建立

在这里插入图片描述

5.模型求解

在这里插入图片描述

6.模型解释

在这里插入图片描述

7.模型应用

之前为离散，而此时视为连续，故计算结果不一致
在这里插入图片描述

8.允许缺货的模型建立

缺货补全，用于补全的产品视作直接被销售，不会贮存
在这里插入图片描述
在这里插入图片描述

但是 Q ′ Q^{'} Q′未考虑补全缺货的生产量，所以即便 Q ′ < Q Q^{'}<Q Q′<Q，仍然有实际意义
在这里插入图片描述

二、森林救火

1.问题背景

在这里插入图片描述

2.问题分析

在这里插入图片描述

3. 模型假设

火势蔓延速度表示 d B d t \frac{dB}{dt} dtdB​的变化率，与 t t t相关，通过积分可以求出损失面积
在这里插入图片描述

4.模型建立

在这里插入图片描述
在这里插入图片描述

5.模型求解

在这里插入图片描述

6.结果解释

在这里插入图片描述

7.模型应用与评注

在这里插入图片描述

三、倾倒的啤酒杯

1.问题背景

在这里插入图片描述

2.问题分析与模型假设

在这里插入图片描述
在这里插入图片描述

3.模型一建立（不考虑杯底）

重心的合成
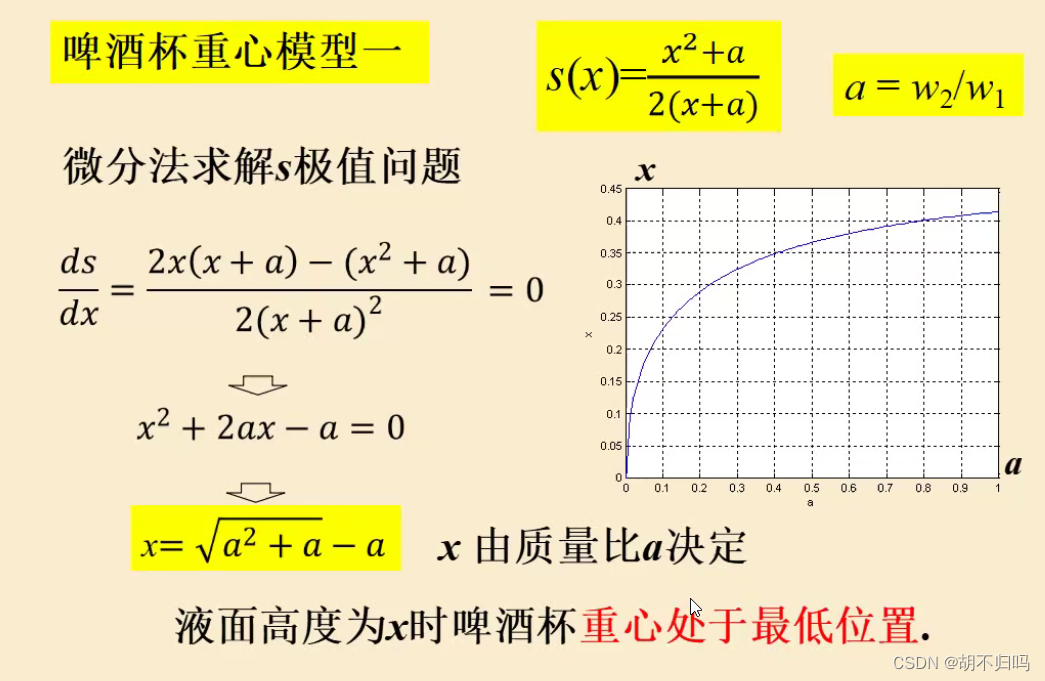
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

4.模型一结果分析

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

5.模型二建立（考虑杯底）

在这里插入图片描述
在这里插入图片描述

6.小结与批注

在这里插入图片描述

四、铅球掷远

1.问题背景

在这里插入图片描述

2.问题分析

在这里插入图片描述

3.模型一建立（不考虑铅球出手的高度）

在这里插入图片描述

在这里插入图片描述

4.模型二的建立（考虑出手高度）

在这里插入图片描述
在这里插入图片描述

5.敏感性分析

在这里插入图片描述
在这里插入图片描述

6.小结与批注

在这里插入图片描述

五、不买贵的只买对的

1.问题背景

在这里插入图片描述
在这里插入图片描述

2.效用函数介绍

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
等值线
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.模型建立

在这里插入图片描述

4.模型求解

寻找相切点，视作连续
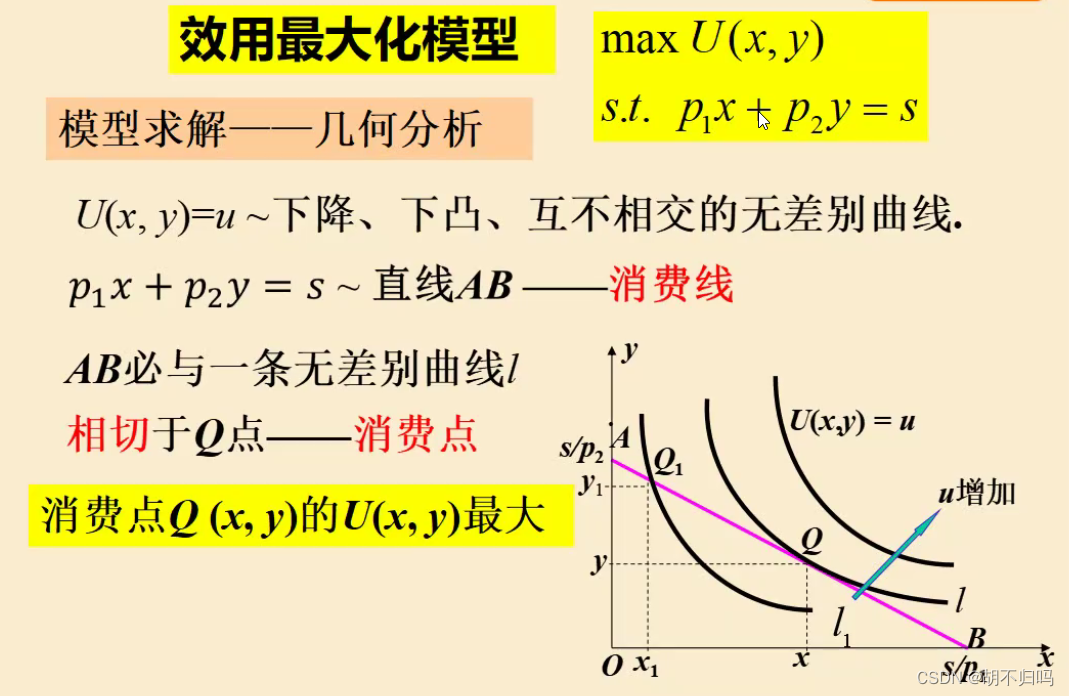
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

5.向n类商品的推广

在这里插入图片描述

6.模型应用

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

贪心思想，选择单位金额边界效用最高的商品
在这里插入图片描述

7.小结与批注

在这里插入图片描述

六、血管分支

1.问题背景

在这里插入图片描述

2.模型假设

在这里插入图片描述
在这里插入图片描述

3.模型建立

在这里插入图片描述

4.模型求解

在这里插入图片描述

5.模型解释

依照最小能量原则推出的结果，提出合理推论
在这里插入图片描述

七、冰山运输

1.问题背景

在这里插入图片描述
在这里插入图片描述

2.问题分析

在这里插入图片描述
在这里插入图片描述
融化速率解释：
在这里插入图片描述

在这里插入图片描述

3.模型假设

在这里插入图片描述

4.模型建立

考虑两种费用和水最终的保留情况，求出最后水每立方米的费用，进行比较
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
离散值，使用枚举法进行比较
在这里插入图片描述

5.模型求解

在这里插入图片描述

6.结果分析

在这里插入图片描述

7.小结与批注

在这里插入图片描述

八、影院里的视角和仰角

1.问题背景

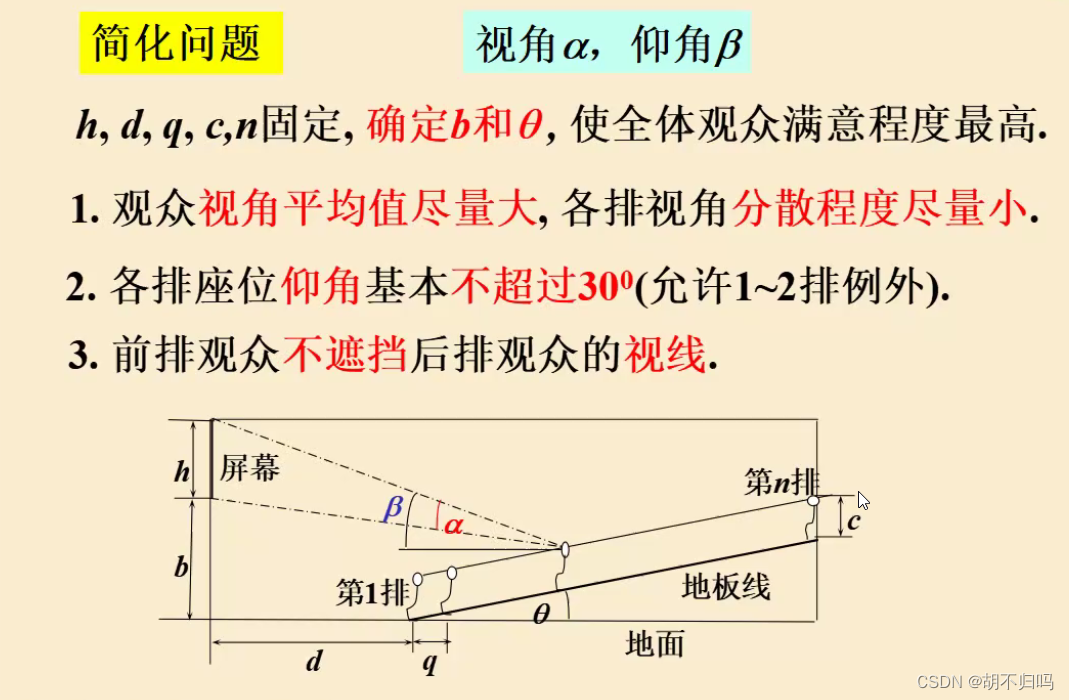
在这里插入图片描述

2.问题分析

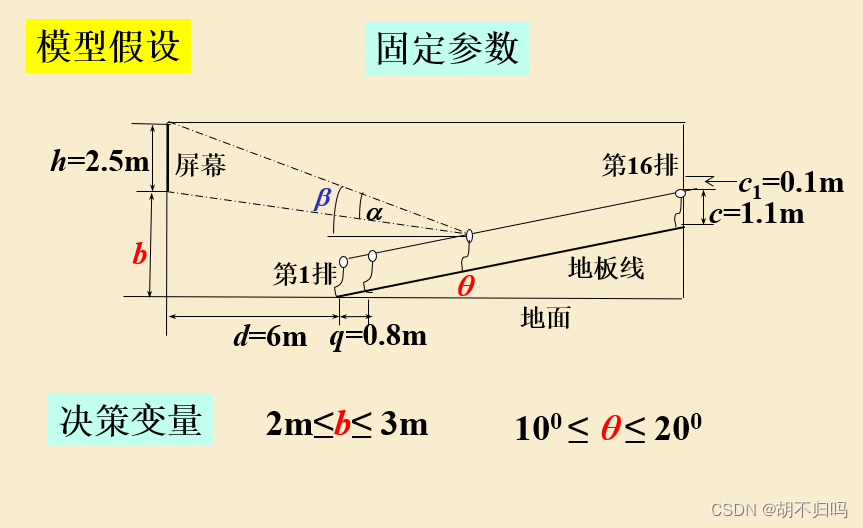
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.模型假设

在这里插入图片描述
在这里插入图片描述

4.模型建立

标准差的求解涉及了概率统计，分母为 n − 1 n-1 n−1与无偏估计有关
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

5.模型求解

微分法难以求解，可以通过离散值的枚举，从中选出最优解
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

6.小结与批注

在这里插入图片描述

数学建模笔记总结
专注大数据与人工智能技术分享，欢迎私信加群互相学习！
05-04 3216
​​​​​​本文主要介绍数学建模常用方法、工具及论文相关模版，正文主要介绍数据建模常见算法及利用python数据分析流程，后续将逐步对每个模型算法展开详细介绍。
数学建模 影院座位设计
03-18
数学建模 习题 影院座位设计 对影院等公共场合的座位进行优化设计
数学建模影院座位设计问题
06-06
关于影，值得一看院座位设计的经典设计问题。详细的解决了该问题
数学建模习题 影院座位优化设计
03-18
数学建模习题 影院座位优化设计 对影院等公共场合的座位进行优化设计
电影院座位的设计 数学建模
07-15
电影院座位的设计应满足什么要求，是一个非常现实的问题。根据题意观众对座位的满意程度主要取决于观看时的视角 和仰角 ， 越大越好，而 越小越好，最佳位置就是要在这两者之间找到一个契合点，使观众对两者的综合满意程度达到最大。
数模3—Matlab线性规划、非线性规划、多目标规划（超全解法合集）
热门推荐
惟愿一生无悔也无憾
09-12 2万+
生产两种机床，利润分别为XXX, A机器和B机器加工，两种机器工作时间…✨若不存在不等式约束，用"[]”代替A和b: [x, fval ] = linprog (f,[],[], Aeq, beq, lb, ub)✨若不存在等式约束，用"[]”代替Aeq和beq: [x, fval ] = linprog Cf,A,b,[],[] ,lb,ub)A机器和B机器加工，有顺序要求，有不同损耗费用，不同的工作时间…每种资产的平均收益率…结论，4个人攻碉楼，2个人追替身的情况下，百姓的士气最大，最大值为220。
数学建模 简单的优化模型
03-18
存储模型、森林救火、最优价格、消费者均衡、冰山运输、生猪的出售时机、血管分支等简单的数学建模优化模型
简单的优化模型
weixin_44936346的博客
07-14 1999
简单的优化模型 以下是根据MOOC西北工业大学肖老师数学建模课程整理的学习笔记（MOOC指路：MOOC数学建模） 1. 两辆平板车装货问题 （1）问题描述 ​ 有其中规格的包装箱要装到两辆平板车上。包装箱的宽和高是一样的，但厚度t（厘米）和重量w（公斤）是不同的。表1给出了每种包装箱的厚度，重量以及数量。 表1 包装箱参数信息： 包装箱类型 C1C_1C1​ C2C_2C2​ C3C_3C3​ C4C_4C4​ C5C_5C5​ C6C_6C6​ C7C_7C7​ 厚度t
数学建模30种基本模型_数学建模中简单的优化模型
weixin_39622562的博客
12-05 2万+
本文介绍较简单的优化模型，归结微积分中函数的机制问题，可以直接用微分法求解。1. 存贮模型 工厂订购原料，出售商品，都需要确定贮存量。 1.1不允许缺货的存贮模型 经济批量订货公式（EOQ公式） 用于订货、供应、存贮情形 每天需求量 r，每次订货费 c1,每天每件贮存费 c2 T天订货一次(周期), 每次订货Q件，当贮存量降到零时，Q件立即到货。1.2允许缺货模型 原理较简单，使用时查...
第三章 简单的优化模型
weixin_45775472的博客
01-27 2961
第三章 简单的优化模型 本章介绍简单的优化模型，归结为微积分中的函数极值问题，直接用微分法求解。 建立优化模型的步骤： 做出若干合理简化的假设 首先确定优化的目标、寻求决策和决策受到的限制 运用数学工具（变量、常数、函数）解决 最后运用微分法求出最优决策 以下选出几个实例学习 1.存贮模型 1.1不允许缺货的存贮模型 问题： 配件厂生产若干种部件，每次生产因更换设备要付生产准备费（与生产数量无关），部件生产大于需求时占用仓库要付贮存费。设计生产计划，确定生产周期，单个周期产量，可使日均
数学建模笔记（一）
weixin_34319111的博客
09-09 998
问题：全国大学生数学建模竞赛2012年A题第一题第一小问——分析附件1中两组评酒员的评价结果有无显著性差异。 工具：Excle、SPSS19中文版 以两组红葡萄酒的评分为例，综合运用t检验、方差分析、χ2检验，符号检验和秩和检验分别求解。其中t检验和方差分析属于参数检验，需要总体服从正态分布且需要检验方差齐性。χ2检验、符号检验和秩核检验属于非参数检验。 1）首先用Excle对原数据进...
数学建模笔记
04-26
数学建模笔记
数学模型（姜启源） 第三章 简单的优化模型
09-19
1．建立数学模型 重点：数学模型的基本方法和步骤 难点：人口模型 2．初等模型 重点：公平席位的分配 难点：实物交换 3.优化模型 重点：存储模型 难点：最优价格 4. 数学规划模型 重点：奶制品的生产模型 难点：奶制品的销售模型 5. 微分方程模型 重点：经济增长模型 难点：经济增长模型 6. 差分方程模型 重点：蛛网模型 难点：蛛网模型 7． 离散模型 重点：层次分析模型 难点：效益的合理分配模型 8． 概率模型 重点：随机人口模型 难点：随机人口模型 9． 统计回归模型 重点：GDP和物价指数 难点：GDP和物价指数
数学建模实验答案_简单的优化模型.doc
10-04
数学建模实验答案_简单的优化模型.doc
数学建模笔记全套资料
12-08
"数学建模笔记全套资料"包含了多种建模方法和技术，这些内容对于理解和应用数学建模至关重要。以下是对这些知识点的详细介绍： 1. **层次分析法 (Analytic Hierarchy Process, AHP)**: AHP是一种结构化决策方法，...
数学建模笔记——动态规划
最新发布
lbm666666的博客
09-11 1753
动态规划的基本想法就是将原问题转换为一系列相互联系的子问题，然后通过逐层地推来求得最后的解。目前，动态规划常常出现在各类计算机算法竞赛或者程序员笔试面试中，在数学建模中出现的相对较少，但这个算法的思想在生活中非常实用，会对我们解决实际问题的思维方式有一定启发。你有三种硬币，分别面值2元、5元和7元，每种硬币都有足够多，买一本书需要27元，如何用最少的硬币组合起来正好付清，不需要对方找钱。虽然我们不知道最优策略是什么，但是最优策略肯定是有k校硬币，，除了这枚硬币，前面的面值加起来是。状态转移方程：对于第。
纽约大学数学建模课笔记：系统化扰动理论分析
### 数学建模笔记知识点 #### 1. 正则扰动理论介绍 正则扰动理论是数学中的一个重要概念，尤其在数学建模和物理学中，当遇到无法精确求解的问题，或者解的形式过于复杂而难以应用时，该理论提供了一种方法来系统地...
数学建模笔记一
叶子心情你不懂
09-25 643
1.1.4 （1） 对于任意的x，存在u， v &gt;= 0 满足x = u - v; |x| = |u + v|。 1）x=0,u = v = 0; x &gt; 0, u = x, v = 0; x &lt; 0, u = 0, v = -x; 也就是u = (|x| + x) / 2, v = (|x| - x) / 2。 （2）Matlabe最后参数可以省略。 functio...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值