KMP的那点事（庖丁解牛）一篇文章彻底看懂KMP算法

最新推荐文章于 2025-04-26 23:01:23 发布

木木木丫

最新推荐文章于 2025-04-26 23:01:23 发布

阅读量1k

点赞数 11

文章标签：算法 c语言数据结构 c++

本文链接：https://blog.csdn.net/qq_52803642/article/details/145609513

版权

背景介绍：

上述题目就是经典的KMP算法的模版题

首先我们介绍传统的暴力做法，不过显示是ac不了这道题的

暴力做法：两个串依次比较

该算法的时间复杂度对于本题而言就是O（mn）

如何优化呢？

对于下面这种情况而言：

当浅蓝色框内的部分匹配，A[5]!=B[4]时：

暴力做法就是 A串 i=2 这个元素与 B串首字母重新进行匹配

显然这个过程每次遇到不匹配的都是A串向前一位 B串从头开始比较非常繁琐

故这里就有大佬创造了 KMP算法！！！！！！！！！！

其核心就是优化上述过程

先简单解释一下 KMP算法主要做了什么工作哈

a b串黑色线之间部分已经匹配，后面一个元素（绿色圈里面的）不匹配

此时暴力做法就是：

a串向后移动一个位置，与b串从头开始比较，及也就是从紫线部分从头开始比较

KMP的思想就是，a串向后最多能移动几个位置，而保证不出错。

这里引入 最长前缀后缀相等 的概念（这里就不详细介绍了帖子很多也很简单以下用数组ne[]表示）

首先证明 x的 存在且必要：

（这部分绿线长度为非负 >=0）即就是不存在匹配的前后缀的串

又因为黑色线之间的部分 a b串本身就是匹配的故可以得到：

ZW这两部分是匹配的

因为x是非负的故一定存在

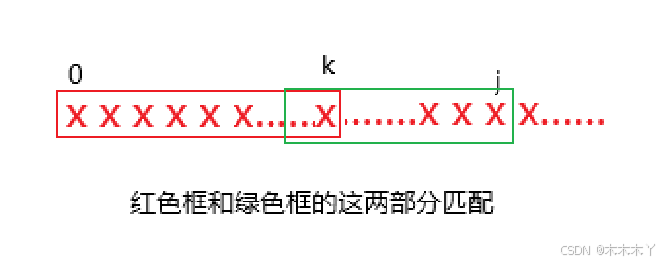
此时直接比较红色框内的这部分即可因为前面已经是配的了

一次KMP在字符串匹配上面的效率很快时间复杂度 O（n）！！！！！

以下这部分重中之重！！！！！！！-

理解了 KMP算法的思想下面主要就是求 ne数组存储前后串匹配位置的数组即可

用到的方法就是 递推的方法

首先解释一下 ne数组里面的数字表示啥：假设ne[ j ]=k;

意思是：数组下标从 0 1 2 一直到 j的这部分其前缀后缀的长度为 k+1

有了这个概念我们定义不匹配为 -1 表达式ne【j】=k；且前缀后缀长度均小于其自身即 k<j

所以已知 ne【0】= -1；

假设j=n时已知，ne【n】=x

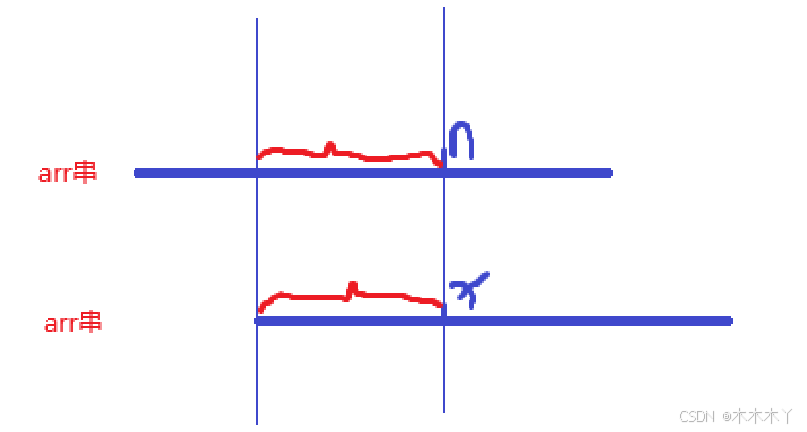
红的括号内的两部分匹配 即为前缀后缀字符串（且为最长哈定义保证了）

注释：其中 n x 为数组下标且数组下标从0开始

来计算j=n+1时有点数学归纳法的意思了哈这也是为啥代码体现为递推

这里就需要分情况讨论了：

第一种情况：arr【n+1】==arr【x+1】

此时ne【n+1】=x+1 结束

第二种情况：arr【n+1】!=arr【x+1】

此时就要自己去寻找 0~ n+1 下标是的最长相等前后缀的位置了

暴力做法（为什么每次都要提到暴力做法，因为好的做法都是从暴力做法去优化出来的！！！！）

首先看挪一步是否匹配：

挪动两步：

………………

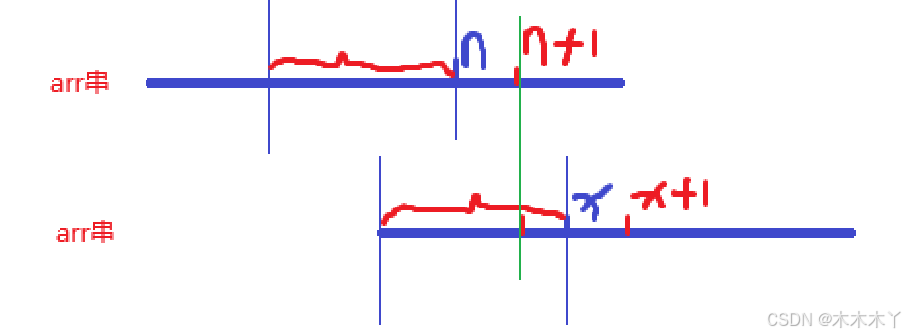
依次向下总到找到 ne【n+1】=y； y=-1,0,1,2……x 最大取到x嘛这里范围也不重要反正能找到就行了。

观察如下关系：

A点坐标n c点坐标为x B点坐标为y-1

绿线与arr的三个焦点分别为1 2 3 注意不是坐标哈

已知的ne【n】=x （我们的假设别忘了）

所以：1A段与2C段是匹配的

又因为 ne【n+1】=y

所以：1A段与3B段是匹配的

所以2C段与3B段也是匹配的所以这个东西出来你们有什么感悟嘛！！

是不是关系就得出来了：

即 B点是A点不断ne【】取出来的结果结束条件就是arr【n+1】==arr【y】当然了 y=-1的话就是不存在这个点（整个移到头就行）

当然了也有找不到的情况：

就是到这应该理解ne数组怎么求了

核心思想就是递推直到ne【0】 ne【1】可以推出ne【2】……一直递推

    //求Next数组 表示最长 相等前缀后缀字符串
    for(int i=1,j=0;i<=n-1;++i)
    {
      while(j>0 && arr[i]!=arr[j] )
           j=Next[j-1]+1;
      if( arr[i]==arr[j])
          j++;
      Next[i]=j-1;
    }

解释一下：因为ne【0】=-1 这是已知的所以 i就从1 开始也可以理解为上下要错开一个

代码不要从头开始分析只要记得我们求 i这个位置时（求ne【i】）前面 0~i-1 是已知的就行

这样方便初学者理解

所以这一步就是我们上面提到的

结束条件有两个找到了这两个点相等或者就是没找到因为没找到 ne【】=-1 所以j=0；

这个意思就是：经过上面我找到了他两匹配是不是就要看下一位是不是匹配所以j++了因为i++ 会在循环条件里面判断所以这里就不用多判断了

这里最后一步就是因为上面我们找到了 ne【i】的值所以来给他赋值

为什么减一呢因为上面我们有个if 使得j++了

如果j=0 就是没找到匹配的所以赋值为-1；

看到这里ne数组就取出来了

最后就是字符串的匹配过程：

#include<iostream>
using namespace std;

const int M=1000010;
const int N=100010;
char arr[N],brr[M];
int Next[N];

int main()
{
    Next[0]=-1;
    int n,m;
    cin>>n;
    scanf("%s",arr);
    cin>>m;
    scanf("%s",brr);
    //求Next数组 表示最长 相等前缀后缀字符串
    for(int i=1,j=0;i<=n-1;++i)
    {
      while(j>0 && arr[i]!=arr[j] )
           j=Next[j-1]+1;
      if( arr[i]==arr[j])
          j++;
      Next[i]=j-1;
    }
    
    


    //匹配过程
    for(int i=0,j=0;i<=m-1;++i)
    {
    
      while(j>0 && brr[i]!=arr[j])
          j=Next[j-1]+1;
    
      if( brr[i]==arr[j])
          j++;
    
        if(j==n)
      {
      printf("%d ",i-n+1);  
         j=Next[j-1]+1;
      }
  
    }
    
    
    
    
    
    return 0;
}

brr为我们被搜索的数组 arr为我们搜索的数组

匹配过程和求ne完全类似因为我们求ne其实就是两个数组来做的这里只不过就是两个数组不一样了

这里还是别从头分析只要写出递推关系就行了

假设i-1 j-1 前面部分匹配来看i j 两个位置如果不相等就一直取arr的 ne数组就行直到这两个位置匹配或者没找到匹配的

如果匹配了就直接就看下一个位置就行

这里的判断条件就与上面求ne数组的地方不太一样

主要就是看我们arr的数组是不是匹配完了

下标都是从零开始到n-1 这里为什么判断n呢

因为上面的if条件如果arr【n-1】匹配了那就会使用j++ 所以会多一个

然后就是打印 brr匹配的起始下标

这里的下一步就是接着搜索

首先来看一下暴力的话这一步怎么写

for(int i=0,j=0;i<=m-1;++i)
    {
    
      while(j>0 && brr[i]!=arr[j])
          j=Next[j-1]+1;
    
      if( brr[i]==arr[j])
          j++;
    
        if(j==n)
      {
      printf("%d ",i-n+1);  
       i=i-n+1;
      j=0;
      }
  
    }

就是 brr数组从匹配位置的下一个点和 arr从头开始我们最开始的那个过程

怎么优化呢画个图就明白了