简单线性回归分析

1. • 理论依据

【基本思想】

1.简单线性回归分析的基本思想

回归分析是定量反映数值型变量之间明显存在的相关关系的一种统计推断方法。回归分析根据自变量的多少可分为简单回归分析和多元回归分析，根据关系类型可分为线性回归分析和非线性回归分析。简单线性回归分析就是在一个因变量与一个自变量之间进行的线性相关关系的统计推断。简单线性回归分析的理论模型为：

2.简单线性回归分析中的拟合优度检验

3.简单线性回归分析中的F检验

4.简单线性回归分析中的残差分析

5.简单线性回归分析中的DW检验

在对回归模型的诊断中，需要诊断回归模型中残差序列的独立性。如果残差序列不相互独立，那么根据回归模型的任何估计与假设做出的结论都是不可靠的。检验残差序列相互独立性的统计量称为DW统计量。

6.简单线性回归分析的基本步骤

(1)由样本数据绘制散点图，判断变量之间是否存在线性相关关系。

(2)确定因变量与自变量，并初步设定回归方程。

(3)估计参数，建立回归预测模型。

(4)利用检验统计量对回归预测模型进行各项显著性检验。

(5)检验通过后，可利用回归模型进行预测，分析评价预测值。

【实验目的】

1.准确理解简单线性回归分析的方法原理。

2.熟练掌握简单线性回归分析的SPSS操作。

3.熟练掌握运用简单线性回归方程进行预测的方法。

4.培养运用简单线性回归分析解决身边实际问题的能力。

2. • 实验内容

20世纪90年代以来，世界已经从工业时代进入了信息时代。工业时代的经济增长多依赖于资本、劳动的投入，而信息时代的经济增长则主要来自科技进步。经济产出函数表现为：Y=AF(K，H，N)。经济的增长不仅依赖于资本(K)、劳动投入(N)，还在很大程度上依靠技术(A)的进步，而要取得技术进步，必须加大人力资本的投入。人才是提高生产率的关键。城市一方面为工业的发展提供基础设施，减少成本，另一方面又为工业的发展提供劳动力和智力支持。因此，城市化会相应增加对人力资本的投入，提高人的综合素质，促进科技进步，提高经济的产出。总之，城市化与经济发展能够相互促进、协调发展，两者具有极为密切的关系，这也是目前各国普遍重视城市化，城市化进程速度加快的根本原因。

国内外很多学者对此作了大量研究，并依据不同变量建立了不同的数学模型进行分析。下面，选取我国1985-2002年的人均GDP和城市化率的时间序列数据，以城市化率作为自变量x，以人均GDP为因变量y，建立一元线性回归模型，得出人均GDP与城市化率之间的回归方程，定量分析两者的内在关系。

本实验中的数据以1985年为可比价，其他年度人均GDP均为价格指数调整之后的真实值(参见数据集“data14-1. sav”)。此数据集中包含年度(n)、人均GDP(y)、城市化率(x)3个变量的21个观测。其中，人均GDP(y)、城市化率(x)均为数值型变量。

3. • 操作步骤

（1）绘制散点图，判断变量之间是否存在相关关系

1）选择菜单:【Graphs】→【Scatter】→【Simple Scatter】。

图6-1：选择菜单步骤

2）弹出如图6-2所示的“Simple Scatterplot”对话框。在对话框中选择人均GDP(元)[y]进入“Y Axis”框内,城市化率(%)[x]进入“XAxis”框内。

图6-2：“Simple Scatterplot”对话框

3）点击“OK”,得出如图6-3所示的输出结果。

图6-3：x与y散点图

4）由图6-3所示的输出结果可以初步判断出人均GDP与城市化率呈线性关系，该数据集适合建立简单线性回归模型。

（2）确定因变量与自变量，初步设定回归方程

以人均GDP为因变量，城市化率为自变量，建立简单线性回归方程：y=β₀+βix+ε

（3）估计参数，确定估计的简单线性回归方程

1)选择菜单:【Analyze】→【Regression】→【Linear】。

图6-4：选择菜单步骤

1. ,弹出如图6-5所示的主对话框，在此对话框中选择变量人均GDP进入“Dependent”框内，城市化率进入“Independent(s)”框内。

图6-5：“linear”对话框

2. 因为只有一个自变量,所以,在“Method”框中选择“Enter”选项即可。

3. 点击“Statistics”按钮,打开如图6-6所示的对话框,该对话框用来定义输出各种常用判别统计量。

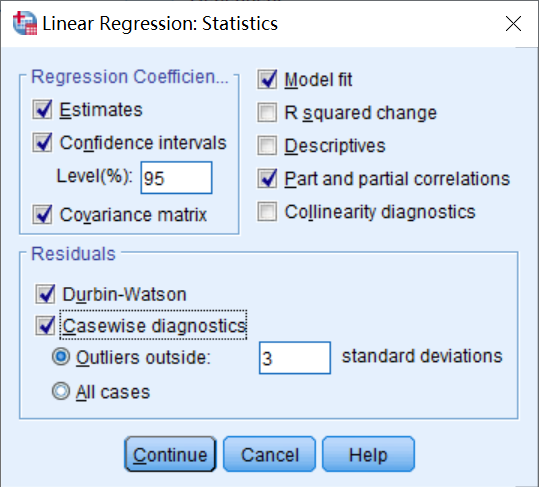
图6-6：“Statistics”对话框

①选择“Estimate”输出回归系数、回归系数的标准差、对回归系数检验的t值，t值双侧检验的P值。

②选择“Confidence intervals”输出每个非标准化回归系数的95%的置信区间;选择“Covariance matrix”输出回归系数的方差。

③选择“Model fit”输出各种默认值：判定系数R²、调整的判定系数、回归方程的标准误差、回归方程显著性的F检验的方差分析表。

④选择“Part and partial correlations”,输出解释变量与被解释变量之间的相关系数。

⑤选择“Durbin-Watson”判断相邻残差序列的相关性。

⑥选择“Casewise diagnostics”进行样本奇异值判断,并在“Outliers outside”的参数框中键入3，设置观测标准差大于等于3的奇异值。

⑦单击“Continue”按钮返回。

4. 在主对话框中点击“Plots”按钮，弹出如图6-7所示的对话框。该对话框主要通过图形进行残差序列分析。

图6-7：“Plots”对话框

窗口左边各变量名的含义如下:“DEPENDNT”表示被解释变量,“”ZPRED”表示标准化预测值,“”ZRESID”表示标准化残差,“”DRESID”表示剔除残差,“'ADJPRED”表示调整的预测值,“‘SRESID”表示学生化残差,““SDRESID”表示剔除学生化残差。

①选取“ZRESID”为Y轴,“ZPRED”为X轴绘制图形研究观测变量的分布规律、异常值，点击“Next”可以选择其他组合进行观察。

②在“Standardized Residual Plots”中选择“Histogram”输出带有正态曲线的标准化残差的直方图，观测残差序列是否服从正态分布。

③选取“Normal probability plot”输出标准化残差图,观测残差波动幅度。

④点击“Continue”返回主对话框。

5. 在主对话框中点击“Save”按钮，弹出如图6-8所示的对话框，该对话框主要是在数据编辑窗口中保存一些变量。

图6-7：“Save”对话框

①在“Predicted Values”框中选择“Unstandardized”,输出由方程计算出的因变量的非标准化预测值。

②在“Distances”框中,选择“Mahalanobis”,计算马氏距离,选择“Cook’s”,计算Cook距离,选择“Leverage values”,计算中心化杠杆值。这三个统计量的计算都是为了找到强影响点和高杠杆点。

③在“Prediction Intervals”框中,选择输出预测区间。选择“Individual”项,输出个别值预测区间。

④在“Residuals”框中,选择“Unstandized”项,输出非标准化残差。

⑤在“Influence Statistics”框中,选择“DfBeta(s)”输出因排除一个特定的观测值所引起的回归系数的变化值。一般情况下，如果此值大于临界值：2/n，则认为被排除的观测值有可能是影响点。

⑥选择“Save to New File”,将回归系数保存在一个指定的文件中。

⑦选择“Export model information to XML file”,可将模型的信息输出到指定的文件夹中。

⑧点击“Continue”按钮,返回主对话框。

6. 在主对话框中点击“Options”按钮，弹出如图6-8所示的对话框，做出有关选择。

图6-8：“Options”对话框

①在“Stepping Method Criteria”框中,选择“Use probability of F”选项,采用F检验的概率值作为依据。系统默认“Entry”值为0.05,“Removal”值为0.10。当一个变量的Sig值≤Entry值时，该变量被引入方程，当一个变量的Sig值≥Removal值时，该变量被从方程中剔除。

②选择“Include constant in equation”选项,在回归方程中加入常数项。

③在“Missing Values”框中,选择“Exclude cases listwise”选项,排除缺失值。

④点击【Continue】→【OK】, 输出全部结果。上述步骤的部分输出结果如下文所示。

（4）全面分析上述步骤的输出结果

分析散点图、残差图判断线性关系是否真实存在，以及模型假设是否成立。根据给定的显著性水平，检验各种统计量的取值及P值。得出有关的回归系数，从而给出估计的简单线性回归方程。

4. • 结果分析

从回归方法输入变量中可以看出，模型采用输入回归法（Enter），该方法在一元回归中不需要过分关注。

表6-1：回归方法输入变量

Variables Entered/Removeda
Model	Variables Entered	Variables Removed	Method
1	城市化率（％）b	.	Enter
a. Dependent Variable: 人均GDP(元)
b. All requested variables entered.

从模型摘要表中可以看出，模型的复相关系数R、R2、调整的R2，调整后模型解释度为97.2%，解释变量与被解释变量之间线性关系明显。

表6-2：模型摘要

Model Summaryb
Model	R	R Square	Adjusted R Square	Std. Error of the Estimate	Durbin-Watson
1	.987a	.973	.972	154.57285	.410
a. Predictors: (Constant), 城市化率（％）
b. Dependent Variable: 人均GDP(元)

线性回归分析不应只关注R方和线性回归方程，要重视数据检验。首先是ANOVA表，通过ANOVA表中的F检验，我们可以了解线性回归分析是否具有统计学意义。下表为回归变量的方差分析，其中F检验的P值为0.000 < 0.05，表明线性关系整体显著，即通过F检验，可以认为一元回归整体线性显著，具有统计学意义。

表6-3：回归模型方差分析表

ANOVAa
Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	16618144.989	1	16618144.989	695.530	.000b
	Residual	453962.564	19	23892.767
	Total	17072107.553	20
a. Dependent Variable: 人均GDP(元)
b. Predictors: (Constant), 城市化率（％）

从表中可以得到非标准化的回归系数、标准化的回归系数、t检验、显著性、置信区间、相关性等。其中城市化率的t检验显著性为0.000 < 0.05，说明回归系数显著，通过t检验，95%的置信区间给出了自变量为（137.012，160.634）的范围。同时自变量与因变量相关性 > 0，说明两者呈正相关。最终，得到模型的表达式为：

表6-4：回归系数及t检验表

Coefficientsa
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.	95.0% Confidence Interval for B		Correlations
		B	Std. Error	Beta			Lower Bound	Upper Bound	Zero-order	Partial	Part
1	(Constant)	-2820.635	180.714		-15.608	.000	-3198.873	-2442.397
	城市化率（％）	148.823	5.643	.987	26.373	.000	137.012	160.634	.987	.987	.987
a. Dependent Variable: 人均GDP(元)

从表6-5中可以得到回归模型的残差统计表，从表中可以知道预测因变量、预测标准差、预测值的标准误差、调整的预测值等统计量的最大值、最小值、平均值、方差、个案数。

表6-5：残差统计表

Residuals Statisticsa
	Minimum	Maximum	Mean	Std. Deviation	N
Predicted Value	707.9625	3577.2734	1861.5547	911.54114	21
Std. Predicted Value	-1.266	1.882	.000	1.000	21
Standard Error of Predicted Value	33.825	73.281	46.514	10.841	21
Adjusted Predicted Value	686.0243	3464.2207	1857.2444	904.14475	21
Residual	-197.27534	389.94891	.00000	150.65898	21
Std. Residual	-1.276	2.523	.000	.975	21
Stud. Residual	-1.344	2.865	.013	1.052	21
Deleted Residual	-218.90964	503.00165	4.31037	176.17894	21
Stud. Deleted Residual	-1.376	3.701	.050	1.178	21
Mahal. Distance	.005	3.543	.952	.944	21
Cook's Distance	.000	1.190	.092	.255	21
Centered Leverage Value	.000	.177	.048	.047	21
a. Dependent Variable: 人均GDP(元)

下图为回归标准化残差直方图，横轴表示与回归相联系的标准化残差，纵轴表示残差的评率，并且右上可以看到标准差和平均值。本题数据符合正态分布的假设。

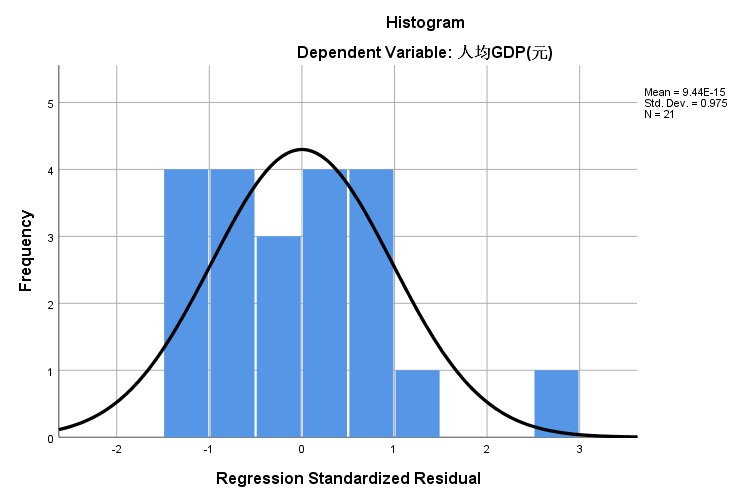
图6-9：回归标准化残差直方图

下图为残差P-P图，横轴是实测累计概率，纵轴表示预期累计概率。由图可见所有散点均匀分布在正方形斜对角附近，表明模型满足随机扰动项服从正态分布这一假设。

图6-9：残差P-P图

下图为残差散点图，本例中反映了GDP作为因变量其散点图的标准化残差。以纵轴0点为对称轴，各散点平均分布在其附近，没有明显的偏正或偏负，也没有表现出明显的规律性，因此可以认为随机扰动项不存在序列相关和异方差问题。

图6-10：残差散点图