UVW运算

在工业视觉中每一个对位项目都会涉及到平台的使用，而UVW平台是较为常见的一种，理解UVW平台的计算规则主要从两个方面的计算出发，其一是平台本身的轴运动方式，其二是实际运动距离与平台轴运动的转换关系。

 一、认识UVW平台

图一

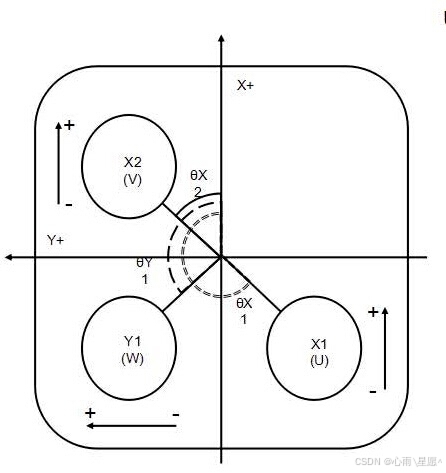
图一是UVW平台的轴运动模式，由UVW三轴构成，这三根轴也被称为X1X2Y1轴。在具体使用中轴运动会体现为平台的平移和旋转，即X方向，Y方向和角度，其中X1X2轴共同控制角度和X方向上的变化，Y1轴单独控制Y方向上的移动。 

 那么，轴是如何控制平台的旋转和移动的呢？每一根轴本身是由电机带动丝杆进行旋转，丝杆每旋转一圈，轴就会运动一定的距离，这个距离称为丝杆导程。而丝杆的旋转需要发送固定的脉冲，每旋转一圈所需要的脉冲量即为脉冲当量，也可以被称为细分。轴运动的运动规则为绝对脉冲，即每次运动前会将先前已有的脉冲量进行累加后以这个累加脉冲进行运动，从而减小了运动误差。丝杆导程由机构提供，脉冲当量由驱动器参数进行设置。

了解了上述的一些基本概念后，问题来了，电机的旋转本身与平台的移动并无联系，软件是如何将这两者关联起来的呢？答案是平台参数。 

图二

 图二为胶片丝印项目使用到的平台参数，胶片丝印项目使用的平台是正方形平台（应该大部分项目使用的都是正方形平台）。其中参数设置为U：255°，V：45°，W：135°，旋转半径为229.810.
结合图一不难发现，轴角度参数的设置就是由图一中的X轴逆时针旋转一定角度到达对应的轴位置。旋转半径则是指平台中心坐标到每一个控制轴运动的电机的距离。

二、UVW运算 

 通过一想必已经对UVW平台有所了解，而UVW运算就是将平台需要移动的距离转换成脉冲发送给电机进行旋转，电机控制了轴的运动从而实现了平台在X，Y，R上的移动。

图三

 我们先从最简单的开始，不考虑角度上的变化。图三要求平台只在X方向和Y方向上移动1mm，可以发现UVW三个轴都移动了1mm（注意，这里使用的是最新版本的视觉软件，UVW运算改成了平台运算，区别在于值由原来的脉冲改为了轴的移动量）。结合图一不难发现X正向移动1就是U轴V轴往正向移动1，Y正向移动1就是W轴正向移动1。

下面对角度进行旋转，正向旋转1° 

图四

 图四所示为正向旋转1°后的结果，UVW的移动量均为2.861，只是运动方向不同，下面我以V轴为例来分析这个数据是如何计算出来的。

图五

 首先确认V轴移动时关联的坐标系轴为X，然后判断正向旋转1°后，V轴的移动方向，不难看出V轴将向负方向运动。可以得出结论，V轴的移动距离就是45°时的X坐标减去46°时的X坐标。接下来就是简单的三角函数运算了：abs(cos(45)*229.810-cos(46)*229.810)=2.860769=2.861，负方向取反为-2.861，即为图四中的V轴结果。

 W轴，U也是一样的
W轴：abs(cos(45)*229.810-cos(46)*229.810)=2.860769，负向取反为-2.861。
U轴：abs(cos(45)*229.810-cos(46)*229.810)=2.860769，正向不变为2.861。

 

---

 反向旋转1°后也是同理
V轴：abs(cos(45)*229.810-cos(44)*229.810)=2.811270，正向不变。
W轴：abs(cos(45)*229.810-cos(44)*229.810)=2.811270，正向不变。
U轴：abs(cos(45)*229.810-cos(44)*229.810)=2.811270，负向取反。

软件计算验证结果无误。

图六

（注意：上述计算使用的都是正向角，你也可以使用反向角进行计算，留意角度大小和轴运动方向即可）

---

以上就是标准的正方形UVW平台的运算方式。当然，如果平台不是正方形而是长方形也是适用的，下面以宽长比为  的长方形平台为例，我们将他正向旋转 10°，如图六所示

图六

该长方形平台的UVW三轴分别旋转了240°，60°和120° 。可以计算得到：

V轴：abs(cos(60)*229.810-cos(70)*229.810)=36.305351，负向取反为-36.305351。
W轴：abs(cos(40)*229.810-cos(30)*229.810)=22.976625，负向取反-22.976625。
U轴：abs(cos(60)*229.810-cos(70)*229.810)=36.305351，正向不变为36.305351。

软件验算无误。 其他宽长比的平台也是同理。

图七

总之，UVW运算本身只是最简单的三角函数运算，只要对平台运动的原理和轴的位置与方向有明确的认知就很容易理解了。