【Coq学习】Formal Reasoning About Programs 阅读笔记第九章_dataflow analysis invariant operations-CSDN博客

本文链接：https://blog.csdn.net/qq_53287459/article/details/134124083

第九章抽象解释和数据流分析 Abstract Interpretation and Dataflow Analysis

对应的coq代码在Abstractlnterpretation.v

前两章展示了如何从一个程序自动建立一个变迁系统（第九章，通过小步语义），以及如何自动找到一个变迁系统的不变量（find an invariant for a transition system automatically）（第八章，模型检测，对状态空间的穷尽搜索自动构造不变量）。现在让我们结合这些思想，用数据流分析（dataflow analysis）的技术（多用于编译器优化），自动找到程序的不变量（find invariants for programs automatically）。本章依然继续使用上一章研究语义时使用的小型命令式语言的例子，以及它用关系代表的基本的小步语义。

命令式语言的例子：

其小步语义：

第八章学的的模型检测，是在系统中建立越来越大的有限可达状态集（finite sets of reachable states）。我们举的命令式语言的例子，状态(v, c)包含了控制状态c（control state c，即下一个要执行的命令）和数据状态v（control state c，即变量的值），因此模型检测会找到限制这两个状态的不变量。我们说模型检测是路径敏感的（path-sensitive），因为它的不变量可以区分与同一个控制状态相关联的不同数据状态，这些数据状态在程序执行过程中沿着不同的路径到达。路径敏感分析往往比路径不敏感分析（path-insensitive analyses）的计算量大得多，路径不敏感分析的不变量包含了到达相同控制状态的所有路径。数据流分析就是这样一种路径不敏感的方法，其基础理论是抽象解释（abstract interpretation）。

根据对程序路径的分析精度来分类：

流不敏感分析（flow insensitive）：不考虑语句的先后顺序，按照程序语句的物理位置从上往下顺序分析每一语句，忽略程序中存在的分支
流敏感分析（flow sensitive）：考虑程序语句可能的执行顺序，通常需要利用程序的控制流图（CFG）
路径敏感分析（path sensitive）：不仅考虑语句的先后顺序，还对程序执行路径条件加以判断，以确定分析使用的语句序列是否对应着一条可实际运行的程序执行路径

9.1 一个抽象解释的定义 Definition of an Abstract Interpretation

抽象解释是一种特殊的抽象，是我们在第八章研究模型检测时讲过的那种抽象。在更一般的情况下，我们可以用任何形式的抽象状态来表示具体状态。在抽象解释中，我们通常将每个变量与一个独立的抽象描述联系起来。举一个稍后会更详细进行形式化的例子：将每个变量标记为“even偶数”、“odd奇数”或“either两者之一”。

定义9.1：对于我们命令式语言的例子，一个抽象解释是一个元组，其中是一个集合（分析的域，the domain of the analysis）；

里面的元素是对数字的所有抽象值。
T 代表Top，是最不具体的抽象值，代表任何具体值。
C 将任何常数映射到其最精确的抽象。
通过算术运算符，计算它们最精确的抽象。
代表join，计算两个抽象值的最小上限（least upper bound）：能代表两个抽象值的任意取值的最具体的值。
形式化了抽象值代表具体值的概念。

对于，定义表示也就是b至少和a一样通范general。一个抽象解释必须满足以下代数定律：

举一个例子：考虑如下奇偶分析的形式化，其正确性的证明留给读者作为练习。(虽然对减法的处理可能看起来不太精确，但我们在这里使用的是自然数而不是整数，因此减法在结果为负的情况下“保持”为零。)

接下来要证明定义的关于奇偶性的抽象解释parity_absint满足抽象解释类型规定的所有laws：

lattice 格的补充知识：

https://www.cnblogs.com/XBWer/p/8005772.html

我们一般认为一个抽象解释是形成一个格lattice（实际上是一个半格semilattice：任意元素都有最小上界（并）或有最大下界（交）），当真的返回其两个参数中最具体（most specific）或最小（least）的上界时，格lattice大致是以运算符为特征的代数结构。我们把奇偶格even-odd lattice可视化为如下的样子：

即：把两个元素连接起来，使我们在格上向上移动，到达它们最低的共同祖先。

一条从a上升到b的边表示举另一个例子，考虑一个跟踪数的质因数的格，直到5，那么图片版本可能是这样的：

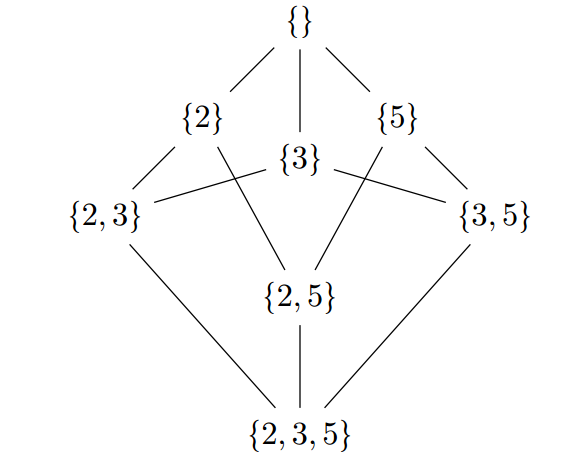
由于显然具有传递性，跨越多个节点的向上移动路径也蕴含着它们端点之间的关系。值得快速验证的是，上图中的任何两个节点都有唯一的最低公共祖先，这是对这些节点进行操作的正确结果。

对于读者来说，另一个值得做的练习是为这个域找出的正确定义。

9.2 流不敏感的分析 Flow-Insensitive Analysis

现在，我们给出从一个抽象解释构建一个程序抽象的方法。我们应用一个流不敏感的抽象（flow-insensitive），这意味着我们找到了一个完全不依赖于一个完整状态(v, c)的控制部分c的不变量。也就是说，不变量只取决于数据部分v。具体来说，代表变量的集合，状态，将域作为我们选择的抽象解释。一个具体的估值映射v的一个抽象状态s为每个x分配一个抽象值s(x)，使得。这里重载操作符，通过来表示这种兼容性。

作为初步定义，我们将一个表达式的抽象解释的语义定义如下：

定理9.2：如果估值映射v和抽象状态映射s满足insensitive_compatible关系，那么算术表达式e的具体值与算术表达式的抽象解释就满足Represents关系。

接下来，我们对命令可能产生的影响进行建模。上面说过，我们的流不敏感分析会忘记一个命令中的控制流，但这在形式上意味着什么？在不考虑控制流的情况下，这种语言的状态只是变量的估值映射（States are just variable valuations），一个命令能影响一个估值映射的唯一方式就是通过执行赋值。因此，忘记命令的控制流相当于只记录它在语法上包含了哪些赋值（recording which assignments it contains syntactically），丢失了有关到达每个赋值需要通过哪些布尔测试（Boolean tests）的所有上下文。这个简单的句法提取过程可以用命令的赋值函数来形式化。

最后，对于抽象状态，通过定义。

现在，只在抽象状态的基础上，我们将流不敏感的步进关系（flow-insensitive step relation）定义为要么什么都不做，要么选一个赋值语句执行，将结果合并到不断增长的候选不变量中：

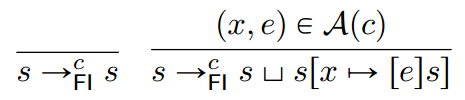
我们可以正式地证明忘记赋值的顺序是一种有效的抽象技术。

定理9.3：给定命令c，初始映射v以及初始抽象状态s，使得。通过在估值映射和抽象状态之间强制执行的模拟关系，使得初始状态为s、变迁关系为的变迁系统模拟了初始状态为(v, c)以及变迁关系为的系统。

现在，一个简单的过程就可以为抽象的系统找到一个不变量：

用定理9.3中描述的抽象状态初始化s。
计算。
如果，那我们就完成了，s就是不变量。
否则，执行赋值然后回到第2步。

上述步骤的每一步都是可计算的（computable），因为抽象状态总是有限的映射（finite maps）。

定理9.4：如果上述的步骤能终止，则“s（来自上面的循环的最终值）是每个可达状态的一个上界”是流不敏感抽象系统的一个不变量。即，对于每一个可达的。

为了检验一个具体的程序，我们首先用定理9.3把它抽象成一个流不敏感的版本，然后用定理9.4找到一个有保证的不变量（a guaranteed invariant）。这里的一个问题是，我们上面写的非正式的循环是否总是会终止并不明显。然而，如果我们的抽象域有有限的高度（finite height），它总是会终止的，这意味着没有无限的不同元素的上升链使得对所有的i都成立。我们之前说的奇偶性的例子很显然具有这个性质，因为它只包含有限多个不同的元素。

值得强调的是，当满足这些条件时，我们的不变量查找过程是保证会终止的，即使底层语言是图灵完全（Turing-complete）的导致大多数有趣的分析问题都是不可计算的（uncomputable）！问题是，找到的不变量总会有可能是一个没多大意义的（a trivial one），其中抽象状态将每个变量映射到。

在下面这个程序中，对流不敏感的奇偶分析给出了最准确的答案（相对于它简化的假设，即我们必须在执行的每一步赋给变量相同的描述）。

我们最终得到的抽象状态是。

9.3 流敏感的分析 Flow-Sensitive Analysis

流敏感分析，是指在分析时，区分程序的执行顺序的分析

流敏感分析，针对的是同一个代码块内部的语句的顺序执行的数据流分析的要求；路径敏感分析，针对的是同一个方法内里面，能够区分不同分支的分析要求（数据流分析是路径不敏感的）

静态代码分析敏感性概念-云社区-华为云

流不敏感的不变量不允许我们为不同行的程序代码记录关于变量的不同事实。这样的分析甚至会被随着我们的前进而变化的变量奇偶性的直接代码所绊倒。下面是一个简单的示例程序，其中流不敏感的分析返回无用的答案，而最准确的答案(关于执行后的程序状态)是：

这个问题的解决方案可以转到流敏感的分析，其中一个抽象状态S是从命令(原始命令的所有中间“程序计数器”)到9.2节的抽象状态的一个有限映射。

程序计数器的功能是存储下一条要执行的指令的内存地址。

定义一个函数来计算从出发经过一步可以到达的所有形如的状态。实际上，对于每一个被非形式化的描述所覆盖的，该函数返回一个从键到值的映射。它的思想就是函数将该步骤包装在没有直接参与该步骤的任何其他命令的上下文中。看看在下面的sequencing的例子中，是如何被修改以达到其目的的：

注意最后的两种条件控制流的情况，完全忽略了测试表达式（test expression），这当然是可靠的(sound，不包含错的结果)，尽管它可能导致分析不精确。这种近似称为路径不敏感性（path insensitivity）。定义来作为的缩写。

现在我们可以定义一个新的抽象步骤关系（a new abstract step relation）：

也就是说，当我们在s中抽象地运行c的结果中查找到键c'对应的值为s'时，我们正好从步进到。

现在，我们可以遵循与上一节中类似的思路。

定理9.5：给定命令c和初始估值映射v。通过一种用于强制命令等价性的模拟关系，以及在估值映射和抽象状态之间的模拟关系，使得初始状态为(s, c) 、变迁关系为的变迁系统模拟了初始状态为(v, c)以及变迁关系为的系统。

将两个流敏感抽象状态的连接写为。当c恰好在之一的域中时，与对应的映射一致。当c不在上述两个域中时，它也不在的域。最后，当c同时在两个域中时，有。

同时，定义表示当，存在使得。

程序步骤如下：

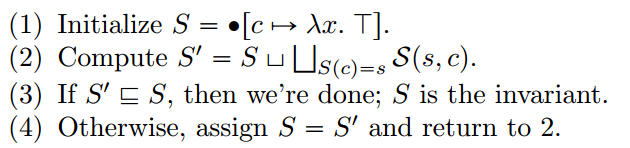
和上一节一样，程序中的每一步都是可计算的。

定理9.6：如果上述步骤能终止，则“对于可达的，对于一些的有”是流敏感抽象系统的一个不变量。

同样，最后两个定理一起为我们提供了在循环终止时自动计算不变量的方法。流敏感的程序保证提供的不变量至少与流不敏感的程序得出的结果一样强，而且通常要强得多。然而，流敏感分析通常在计算上(在时间和内存上)要昂贵得多，因此需要权衡。

9.4 拓宽 Widening

考虑区间（intervals）的一个抽象解释，其中域的每一个元素都是的形式，。出于阐述的目的，将a和b的值限制在0和1之间，我们有下面这个域的图（diagram of the
domain），其中最下面的元素表示一个空集。

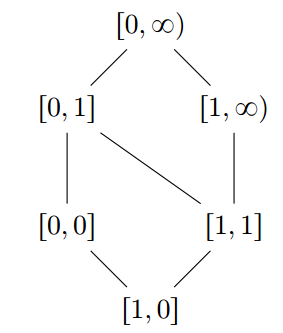
抽象运算符（abstract operators）具有直观而简单的定义，例如，将不同类型的区间展平为一个共同的记号，按照通常的和做算术的含义来定义

同样，上面的格图被简化为只包含作为合法常量的0和1。我们可以定义区间格，从完整的、无限的自然数集合中绘制。在这种情况下，我们很快就会陷入抽象解释的困境。例如，考虑这个无限循环程序：

一个(流不敏感的)不变量是，表示为抽象状态。然而，即使是流敏感的分析，当它一遍又一遍地遍历循环时，也会不断扩大a的范围！我们看到a初始化为[7, 7]，然后在一次循环迭代后增长到[7, 10]，然后在另一次迭代后增长到[7, 13]，以此无限类推。

注意，之前提到，当格具有有限的高度时，终止是有保证的，而我们刚刚展示了这对于一般的区间是不成立的，因为我们的示例程序生成了不同区间的无限上升链。

补充：

可靠性Soundness：不包含错的结果。

对于提出的东西，我把它拿去验证具体情况，结果都对。从抽象到具体

完备性completeness：包含所有对的结果。

我拿具体的所有情况去验证你提出的东西是否都满足。从具体到抽象

证明时属于两个不同的方向

这个问题的标准解决方案是使用一个扩展操作符（widening operator）。该运算符具有与相同的可靠性（soundness）要求，但我们不要求它给出其两个操作数的最小上界。它只需要给出某个上限（some upper bound）。事实上，我们不希望它给出最小的上限；我们希望它在必要时跳过该顺序（skip ahead in that ordering），以促进终止。通常，我们不想把所有的都替换为。例如，我们可能只对循环开始的命令用代替，以保证程序中没有无限的路径避免与的无限多次相遇，以避免无限的上升链。