【Coq学习】Formal Reasoning About Programs 阅读笔记第十章

本文链接：https://blog.csdn.net/qq_53287459/article/details/134978992

第十章通过Simulation Arguments证明编译器的正确性 Compiler Correctness via Simulation Arguments

补充：

编译器是一种计算机程序，它将一种高级程序设计语言（源代码）翻译成另一种目标语言（通常是机器代码或中间代码）。编译器是软件开发过程中的关键组件之一，它在程序的构建阶段起到重要作用。

以下是编译器的主要功能和工作流程：

词法分析（Lexical Analysis）： 编译器首先对源代码进行词法分析，将源代码分割成一个个的词法单元，例如标识符、关键字、运算符等。

语法分析（Syntax Analysis）： 接下来，编译器进行语法分析，检查词法单元之间的语法结构，生成抽象语法树（AST）表示源代码的结构。

语义分析（Semantic Analysis）： 在语义分析阶段，编译器检查程序的语义，确保它在逻辑上是正确的。这包括类型检查、作用域分析等。

中间代码生成（Intermediate Code Generation）： 编译器生成一种中间表示形式，通常是一种抽象的、与机器无关的中间代码。这有助于简化后续的优化和目标代码生成阶段。

优化（Optimization）： 编译器执行各种优化技术，改进中间代码以提高程序的性能。优化可以包括常量折叠、循环优化、内联等。

目标代码生成（Code Generation）： 编译器将中间代码翻译成目标机器代码或其他形式的可执行代码。

链接（Linking）： 在某些情况下，编译器可能需要将多个源文件生成的目标代码链接在一起，以创建最终的可执行文件。

确保编译器正确转换源代码并生成高效的目标代码对于软件的正确性和性能至关重要。"Compiler Correctness via Simulation Arguments"可能是一种方法，通常涉及形式化的证明和推理技术。

操作语义的一个很好的应用是编译器转换的正确性。编译器由一系列阶段组成，每个阶段将某种源语言的程序翻译成某种目标语言。通常，在编译器的大多数阶段，源语言和目标语言是相同的，这些阶段通常被视为优化，在实践中往往会提高大多数程序的性能。当源语言和目标语言相同时，验证问题已经足够困难了，所以我们将在本章中将注意力集中在单一语言上。它几乎与前两章中的命令式语言相同，但我们增加了一个新的句法结构，如下所示。

命令out(e)输出表达式e的值，例如通过将其写入终端窗口。添加输出的有趣之处在于，现在不同的非终止程序具有不同行为：它们可能生成不同的输出序列，有限的或无限的。任何编译器阶段都应该保持输出行为不变。值得注意的是，我们的主力不变量技术在这方面不能直接帮助我们。输出等价性只能通过观看程序的完整运行来判断。但对于一个不终止的程序，就算到了某个点满足了我们选择的不变量，之后的运行可能仍然存在不满足不变量的情况。虽然安全性质（safety）的不变量是完备的（complete），但在这里，我们第一次系统地研究了一类活性性质（liveness）。我们还必须深入研究建立程序的关系（relational）属性，这意味着我们对两个不同程序的执行之间的联系进行推理。在我们的例子中，这样的一对程序即包括输入到一个编译阶段的程序，以及该阶段生成的程序。

安全性是指程序不会达到坏的状态，而活性是指程序最终达到一个好的状态。

为了开始形式化地表述正确性条件，我们需要修改我们的操作语义以跟踪输出。为此，我们采用一种带标签的变迁系统，在该系统中，步骤箭头用标签来注释，以解释与世界的互动。对于这种语言，唯一的交互类型是输出，我们将把它写成一个数字。我们也有静默标签（silent label），用于在没有输出时使用。为了完整性，下面是扩展语言的完整规则，其中上下文和插入操作符的定义继承之前8.3节上下文小步语义的定义。

为了对无限执行进行推理，与之前基于不变量的证明相比，我们需要一个新的抽象：traces，它是程序可能生成的输出序列(和终止事件)。我们归纳地定义一个命令的trace set。和第3章提到的一样，·表示是一个空列表，而执行列表的连接操作。

注意，trace可以在任何点结束，即使程序尚未终止。此外，由于我们的语言是确定性的，对于一个命令的任意两个traces，一个trace是另一个trace的前缀。然而，我们在这里建立的机制的许多部分也能很好地适用于不确定性系统，正如我们将在第21章看到的带标签的并发变迁系统一样。

定义10.1：trace的包含关系：对于命令c1和c2，当且仅当c1产生的trace包含于c2产生的trace时，定义

定义10.2：trace的等价关系：对于命令c1和c2，当且仅当c1产生的trace等于c2产生的trace时，定义

也就是说，对于本章确定性的程序，编译正确性应该遵循输出程序与输入程序具有相同的trace。

10.1. 基本Simulation Arguments和优化表达式 Basic Simulation Arguments and Optimizing Expressions

常量折叠（Constant Folding）、循环优化（Loop Optimization）和内联（Inline）是编译器中两种常见的优化技术，它们旨在提高生成的目标代码的效率。

常量折叠（Constant Folding）：

定义： 常量折叠是一种编译器优化技术，它在编译阶段对表达式中的常量进行计算，并将其结果替代为单一的常量值。
例子： 考虑表达式 2 + 3 * 4，常量折叠会计算乘法操作，将其简化为 2 + 12，最终得到结果 14。这样可以在编译阶段就避免在运行时进行相同的计算。

循环优化（Loop Optimization）：

定义： 循环优化是通过修改循环结构或优化循环体内的代码，以提高循环执行的效率的一类编译器优化技术。
例子：
循环展开（Loop Unrolling）： 将循环体内的代码复制多次，减少循环迭代的开销，但可能增加代码大小。
循环合并（Loop Fusion）： 将多个相邻的循环合并为一个循环，减少循环的开销。
循环变量分析（Loop Invariant Code Motion）： 将循环内部与循环无关的计算移到循环外，避免重复计算。

3. 内联（Inline）：

定义：是一种编译器优化技术，它用于在调用函数的地方直接插入函数体，而不是通过常规的函数调用机制来执行。这样做的目的是减少函数调用的开销，提高程序的执行效率。内联通常应用于短小的函数或频繁调用的函数。

这些优化技术旨在减少程序运行时的时间和空间开销，提高程序的整体性能。编译器通过分析源代码并应用这些优化技术，可以生成更为高效的目标代码。

第一个编译器阶段的示例，我们考虑一种有限形式的常量折叠，其中具有静态已知值的表达式被常量替换。整个优化过程是(1)找到所有不包含变量的最大程序子表达式，(2)用已知的常量值替换每个这样的子表达式。将在命令c上应用此优化的结果记为。(对于本章中的程序转换，这里只对它们如何操作进行非形式化的描述，细节将留给附带的Coq代码。)

与原始的、未优化的程序相比，以这种方式优化的程序以一种非常有规律的方式进行。小步骤一一排列。因此，原始程序和优化后的程序满足模拟关系。(这个概念与第7.2节Abstracting a Transition System中的概念非常相似，不过现在它包含了标签。)

定义10.3：模拟关系：我们称目标语言状态上的二元关系R为模拟关系当且仅当以下两个条件成立：

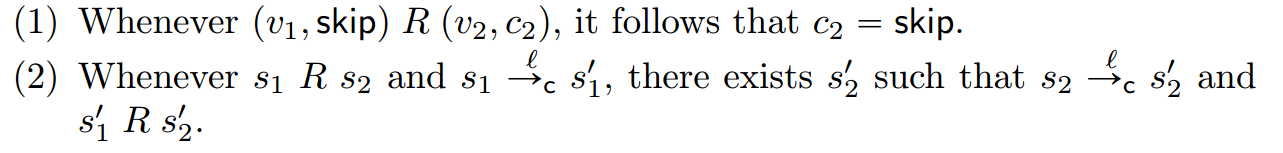
非常关键的第二个条件可以用下图表示：

上图告诉我们，当存在沿左侧的路径到时，也存在匹配的右边路径到。也就是说，左边的任何一步都可以与右边的一步相匹配。注意与我们到目前为止主要依赖的不变量归纳法原理的相似性。我们没有说明每一步都满足一个单状态参数的谓词，而是说明了每一步都以一种特定的方式满足了一个双状态参数的谓词。对于关联程序，模拟方法是通用的，就像不变量方法用于验证单个程序一样。

定理10.4：如果存在一个模拟关系R使得成立，那么状态s1和s2满足trace等价性。

证明思路：

分别证明两个trace包含的方向：从左到右的方向是通过对左侧trace定义的归纳来进行的，而从右到左的方向是通过在右侧进行类似的归纳来进行的。虽然大多数证明在带标签的变迁系统的细节上是通用的，但对于从右到左的方向，我们确实依赖于这种目标语言的两个重要性质的证明：首先，语义是完全的（ semantics is total），即：命令不是Skip的任何状态都可以执行一步；其次，语义是确定的（ semantics is deterministic），因为从特定的起始状态在一个步骤中最多可以到达一个标签或者状态对（label/state pair）。

在从右到左包含证明的归纳步骤中，我们知道右边的系统已经往前进了一步。左边的系统可能是Skip，在这种情况下，根据模拟的定义，右边的系统必定也是一个Skip，这与右边的步骤的假设相矛盾。否则，根据语义是完全的（ semantics is total），左边的系统可以走一步。根据模拟的定义，右边存在一个匹配步长。根据确定性（ determinism），匹配步骤与我们已经知道的步骤相同。因此，我们有一个新的R关系连接到这一步并应用归纳假设。

我们可以将这个非常普遍的原理应用于常量折叠。

定理10.5：对于任意的v和c，状态(v,c)和状态(v, cfold1(c))的trace是等价的。

证明方法：通过使用如下关系的 simulation argument:

我们所做的是把原来的定理陈述转换成二元关系的语言，因为这个简单的例子不需要等价的强化归纳假设。在证明的内部，我们需要定义估值上下文C的常量折叠，并且我们需要证明原始步骤在改变后可以在常数折叠的状态上使用，这是通过对推导的不同情况分析进行的第二个证明。另一个更明显的工作是一个引理，它表明表达式的常量折叠遵循了语义解释的结果。

10.2. 允许跳过步骤的模拟 Simulations That Allow Skipping Steps

考虑上述常量折叠优化的一个扩展：利用IF条件判断表达式的已知值，根据值是否为零，我们可以将整个IF语句替换为它的两种分支情况之一。我们将这个扩展的优化记为，并努力证明它的可靠性。然而，我们不能再使用上一节对模拟的定义，因为这个优化有意减少了程序需要执行的步骤。源程序的一些步骤现在在目标程序里找不到相应的匹配步骤，比如当我们单步执行具有已知值的IF条件判断表达式时。

让我们先来看看如何使模拟更加灵活。

定义10.6：(允许跳过步骤的模拟关系(错误版本!))。我们说，对象语言状态上的二元关系R是一个允许跳过步骤的模拟关系当且仅当以下两个条件成立：

和上一节定义的模拟关系的不同之处在于第二条的(b)，也就是当一个命令没有任何输出且执行该步得到的后续命令依旧和先前的s2满足模拟关系，即当原系统状态走silent的一步时，模拟系统的相应状态不用做任何改变也依然满足模拟关系。换句话说，为了匹配一个无声的步骤，只要之后R仍然成立，它什么都不做也可以。

我们并没有无缘无故地将该定义标记为错误版本，因为它实际上并不蕴含trace等价。考虑一个有问题的“优化”，定义为“withAds( while 1 do skip) = while 1 do out(0)，withAds(c) = c” 用于所有其他c。它向特定的无限循环中添加了一个额外的输出值0。现在我们定义一个候选模拟关系。

这种可疑的关系没有记录任何关于c2的信息。模拟的跳过条件被处理得很简单，R不允许c1=skip。检查模拟的执行匹配条件，c1要么是while 1 do skip，要么是（skip;while 1 do skip），每一步都silently走到另一步。我们可以通过保持c2在适当的位置来匹配任一步，因为R根本不约束c2。因此，R是允许跳过步骤的模拟关系，并且，对于c=while 1 do skip时，它将c与withAds(c)关联起来。从这里，我们期望得出trace等价的结论。然而，显然withAds可以将一个从不输出的程序变成一个无限频繁输出的程序！

让我们修补一下我们的定义。

定义10.7：