【Coq学习】Formal Reasoning About Programs 阅读笔记第一章第二章

Present*

已于 2024-01-08 09:31:18 修改

阅读量961

点赞数 1

分类专栏：程序形式化推理FRAP（Coq学习）文章标签：学习

于 2023-02-09 01:07:08 首次发布

本文链接：https://blog.csdn.net/qq_53287459/article/details/127186625

版权

程序形式化推理FRAP（Coq学习）专栏收录该内容

8 篇文章

订阅专栏

《Formal Reasoning About Programs》是MIT的一个计算机科学的教授Adam Chlipala写的，是一本非常经典的关于程序形式化推理的书，阅读本书需要一定的数学和计算机科学基础。此外，这本书是使用 Coq 作为主要的形式化推理工具，因此在读书之前需要先熟悉 Coq 的基本概念和语法。可以从 Coq 官方网站下载 CoqIDE，并跟随官方文档和教程学习 Coq 的基本语法和证明策略。

全书共22章，148页，书中的案例研究都提供了相应的 Coq 代码和证明脚本，可以自己动手编写和运行这些代码，并逐步理解其中的推理思路和技巧。

书和源代码的下载网址：

Formal Reasoning About Programs

Coq官网：

Welcome! | The Coq Proof Assistant

摘要

简要介绍了这本书的内容主要是关于一种使软件工程跟上更传统的工程学科的方法，为实际的计算机系统的严格分析提供数学基础。

比如土木工程师会运用他们的数学准则来确定桥梁不会倒塌，软件工程师也应该运用不同的准则来证明程序运行正常。其他工程学科都有计算机辅助设计工具，计算机科学也有用于逻辑论证的证明助手和集成开发环境。这本书就将介绍如何应用这些工具来证明程序的行为符合预期。

具体来说，本书主要介绍两个相互关联的主题：

(1) 用于机器检查数学定理证明的工具：Coq证明助手

(2) 关于程序正确性的形式化逻辑推理

第一章为什么要证明程序的正确性 Why Prove the Correctness of Programs?

作者阐述了程序的正确性证明相当于建立一个相应的公认标准，在程序被应用之前，能够获得对程序的安全性、可靠性和正确性的信心。

程序正确性证明的相关概念和工具可能还没有完全准备好被广泛的采用，但它们已经发展了几十年。因此这本书介绍一种特殊的工具也就是Coq，以及如何把它应用到程序证明的不同任务当中的一系列思想。

我们会通过这本书学习各种不同的方法来形式化一个程序应该做什么，并证明一个程序做了它应该做的事情。这些学习内容是基于两个common foundations：一方面，本书会使用Coq证明助手来证明所有的定理。Coq是一个用于编写和机器检查证明的强大框架。Coq本身基于一个相对较小的核心功能，很像一种设计良好的编程语言，在此之上越来越复杂的抽象构建为库。Coq的core features核心功能可以被认为是所有数学推理的核心。

另一方面是程序证明通常会考虑的4个元素：

1、编码。每一种编程语言都有句法和语义，句法定义了程序长什么样子，语义定义了程序运行时的行为。之所以会考虑这个元素，是因为在定义句法和语义时，有时看似微小的决定可能会对我们后续的证明是否顺利产生重大影响。

2、不变量。几乎每一个关于程序的定理都是以一个转换系统的形式表述的，系统有一些状态集和一个状态间的转换关系。几乎每个程序证明都是通过寻找转换系统的不变量，或者是每个状态都保持成立的一个属性来进行证明的。不变量的概念非常接近于数学归纳法的思想，也就是归纳的起点满足的属性在归纳组装的过程中一直保持成立。

3、抽象化。通常，由于转换系统太复杂而不能直接分析。因此，需要将它抽象为另一个更易于处理的转换系统，然后证明新系统保留了原始系统的所有相关属性。

4、模块化。当一个转换系统过于复杂时，我们还可以将其分解为单独的模块，然后使用一些组合操作符将它们重新组合成一个整体。通常抽象化和模块化是同时使用的，也就是我们可以使用模块化把系统分割成更易于管理的部分，再通过抽象以保留关键属性的方式来简化部分。我们甚至可以交替使用这两个策略，先将一个系统模块化，分解为多个部分，然后将分解后的部分抽象为更简单的部分，再进一步将该部分模块化分解为多个部分，等等。

（抽象能省略细节，模块化能专注特定部分，提高效率。）

这本书不会完全正式地定义以上这些技术，而是提供很多例子，对这些例子进行概括，可以帮助读者对何时使用每个元素以及应用的常见设计模式建立一种直觉。

最后的两段内容说明本书遵循一组特定的统一术语和符号，这些符号约定几乎都是用LATEX实现的。此外，本书的每一章都有一个相应的Coq源文件。当本书给出定理和引理陈述时，很少给出它们的书面证明，但所有证明都可以在附带的Coq源代码中找到。

第二章形式化程序的句法 Formalizing Program Syntax

2.1 具体的句法 Concrete Syntax

一个程序的定义是从编程语言的定义开始，而编程语言的定义从它的句法开始。句法规定了哪些类型的短语是符合格式要求的。下一章会介绍语义，也就是说明程序的含义，它可能会施加进一步的有效条件。目前这章我们从具体的句法开始，它规定了哪些字符序列是可接受的。举例来说，对于简单的算术表达式语言，我们接受下面这些字符串是有效字符串。

还有很多其他字符串可能是无效的，比如下面这些：

接着我们用BNF范式的语法去形式化上面的具体的句法。BNF是推导规则也就是产生式的集合，定义的左边是符号也就是指非终结符，右边是使用符号的表达式，可以由竖杠分隔的多个符号序列构成。有些符号是通过使用现有的集合来定义的，比如下面的常量集n是用已知的自然数集合N来定义的。

因此以上表达式的定义就包含了常量、变量、加法和乘法。加法和乘法可以递归的用较小的表达式构建更大的表达式。

这里作者提到本书最重要的工具之一是归纳定义，解释如何从较小的集合构建更大的集合。上述语法的递归性质隐含地给出了归纳定义，因为递归的终点就是归纳的起点。归纳定义的一个更通用的表示法提供了一系列定义一个集合的推理规则inference rules 。用这个推理规则表示的话，集合的定义就是满足所有规则的最小的那个集合。这里每条规则都有前提和一个结论。我们可以用以下的四个规则来等价定义上面的BNF语法定义的Exp集合。推理规则的读法是: 如果线上方的前提成立，那么线下方的结论也成立。对于元变量比如n和e1的所有取值，规则都要保持成立。就相当于线上方每个元变量前面都有个隐式的全称量词一样。

2.2 抽象的句法 Abstract Syntax

对我们人的大脑来说，文本字符串比较自然简单，但要完全形式化的处理它们就很麻烦，因此更喜欢用抽象的句法。我们考虑程序的抽象语法树，也就是以树状的形式表现编程语言的语法结构，它对应于Coq中的归纳类型定义或者Haskell里面的代数数据类型。下面枚举了算术运算那个例子在coq语法里面的构造函数以及它们的类型。这就定义了Exp集合所包含的元素就是由这些构造子函数构造出来的。

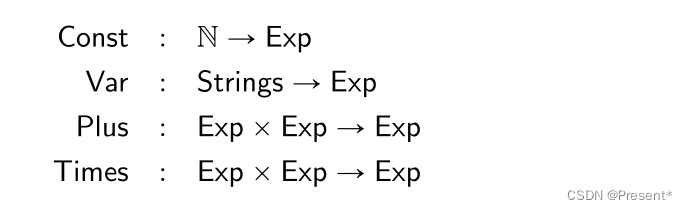
这里的符号表示笛卡尔积，也就是表示前一个Exp集合中的成员作为第一元素，后一个Exp集合中的成员为第二元素构成的所有的有序对组成的集合。

对应的Coq代码定义：

  (* The following definition closely mirrors a standard BNF grammar for expressions.
   * It defines abstract syntax trees of arithmetic expressions. *)
  Inductive arith : Set :=
  | Const (n : nat)
  | Plus (e1 e2 : arith)
  | Times (e1 e2 : arith).

  (* Here are a few examples of specific expressions. *)
  Example ex1 := Const 42.
  Example ex2 := Plus (Const 1) (Times (Const 2) (Const 3)).


(* Let's shake things up a bit by adding variables to expressions.*)
  Inductive arith : Set :=
  | Const (n : nat)
  | Var (x : var) (* <-- this is the new constructor! *)
  | Plus (e1 e2 : arith)
  | Times (e1 e2 : arith).

  Example ex1 := Const 42.
  Example ex2 := Plus (Const 1) (Times (Var "x") (Const 3)).

知识点补充：

抽象语法树（Abstract Syntax Tree，AST），或简称语法树（Syntax tree），是源代码语法结构的一种抽象表示。 树上的每个节点都表示源代码中的一种结构。之所以说语法是“抽象”的，是因为这里的语法并不会表示出真实语法中出现的每个细节。

过程：

先对原始语进行词法分析获得token表之后，再使用语法分析，将一维无结构的token表转化为树形结构。

作用：

通过操纵这棵树，我们可以精准的定位到声明语句、赋值语句、运算语句等等，实现对代码的分析、优化、变更等操作。

例子：

AST抽象语法树的基本思想_孙新404的博客-CSDN博客_ast树

statement_list语法单元，用来表示子节点都是并列依次执行的语句

用推理规则的语法表示的话就是下面这样，和之前提到的相比就是结论都用了构造子函数。

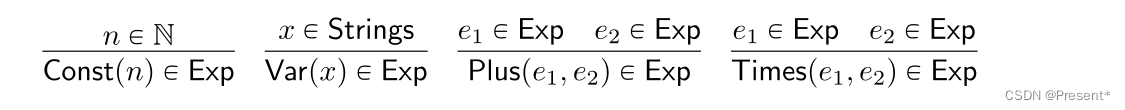
纸上的证明不方便写这种冗长的描述，都是用的具体的句法相关的那些符号。但是coq代码都是从抽象的句法开始的。本书后面的例子就不特意关注这个转换过程了，而是直接用抽象的句法介绍coq相关的代码。

抽象的句法便于编写函数的递归定义。下面举例了一个递归定义的例子。

对应的Coq代码定义：

  (* How many nodes appear in the tree for an expression?
   * Unlike in many programming languages, in Coq,
   * recursive functions must be marked as recursive explicitly.
   * That marking comes with the [Fixpoint] command, as opposed to [Definition].
   * Note also that Coq checks termination of each recursive definition.
   * Intuitively, recursive calls must be on subterms of the original argument. *)
  Fixpoint size (e : arith) : nat :=
    match e with
    | Const _ => 1
    | Plus e1 e2 => 1 + size e1 + size e2
    | Times e1 e2 => 1 + size e1 + size e2
    end.

  (* Here's how to run a program (evaluate a term) in Coq. *)
  Compute size ex1.
  Compute size ex2.

(*******************************************************************)

  Fixpoint size (e : arith) : nat :=
    match e with
    | Const _ => 1
    | Var _ => 1
    | Plus e1 e2 => 1 + size e1 + size e2
    | Times e1 e2 => 1 + size e1 + size e2
    end.

  Compute size ex1.
  Compute size ex2.

这里很重要的一点是每个归纳类型的构造子函数都要有一个子句，否则的话这个递归定义的size函数就不是完全函数，而是偏函数，也就是存在有函数的输入没有与之对应的输出值。例子中size函数的输入就是构造子函数。

另外为了确保终止，只对构造子函数的参数进行递归调用。Coq采用的终止准则叫做原始递归primitive recursion。

原始递归函数：原始函数或者原始函数经过复合或递归得到的函数。

原始递归函数有个特点是: 它总能停机。所以在设计一个类型系统或者自动证明机的时候, 就会尽量在原始递归函数的基础上定义类型运算, 这样编译器就能保证停机了。

下面是举例说明我们可以在定义递归函数的时候直接写新的符号记法。

类似的我们可以用另一个新的符号表示Exp集合里的元素e的深度，也就是也就是从语法树的根节点到任意叶子节点的最长路径。

对应的Coq代码：

  (* What's the longest path from the root of a syntax tree to a leaf? *)
  Fixpoint depth (e : arith) : nat :=
    match e with
    | Const _ => 1
    | Plus e1 e2 => 1 + max (depth e1) (depth e2)
    | Times e1 e2 => 1 + max (depth e1) (depth e2)
    end.

  Compute depth ex1.
  Compute depth ex2.

(************************************************************************)

  Fixpoint depth (e : arith) : nat :=
    match e with
    | Const _ => 1
    | Var _ => 1
    | Plus e1 e2 => 1 + max (depth e1) (depth e2)
    | Times e1 e2 => 1 + max (depth e1) (depth e2)
    end.

  Compute depth ex1.
  Compute depth ex2.

2.3 结构归纳原理 Structural Induction Principles

说到归纳法，我们最熟悉的是对自然数的数学归纳法。但这本书不会详细讨论关于自然数的许多证明，而是提出更普遍和更强大的结构归纳法的思想。如果将自然数视为一个简单的归纳定义的集合，那么结构归纳法在形式意义上也包含数学归纳法。

保持成立就是在构造前成立的, 构造后也成立。

chrome-extension://cdonnmffkdaoajfknoeeecmchibpmkmg/assets/pdf/web/viewer.html?file=https%3A%2F%2Fcourses.engr.illinois.edu%2Fcs173%2Ffa2010%2FLectures%2Ftrees.pdf

对比数学归纳法来说，结构归纳不用找一个归纳变量，而是遵循集合元素递归定义的结构。

从归纳定义到相关的归纳原理有一个通用的方法。当我们归纳定义集合S时，我们得到了一个归纳原理来证明某个谓词P对S的所有元素都成立。为了得到这个结论，我们必须对归纳定义的每个规则都进行一个证明。拿上面的关于集合Exp的抽象语法的推理规则来说，为了推导出一个Exp结构归纳原理，我们对推理规则做两个关键的修改：

（1）对于结论中E属于S的形式，都要替换为P(E)，也就是要证明P对特定的项保持成立。

（2）对于前提中每个E属于S的形式，都增加一个前提P(E)，也就是假设P对特定的项保持成立。每个这样的假设就称为归纳假设inductive hypothesis (IH)。

*************************************************************************************************************

修改后就产生如下所示的4个proof obligations和与之相关的归纳证明：。

也就是说，为了建立这个证明，我们需要证明这些推理规则中的每一个都是有效的。下面作者举例证明了一个定理，对前面的两个递归定义进行了完整性检查: 深度永远不能超过大小。

证明遵循Exp集合元素e的归纳定义结构，分为4部分：

如果e是一个Const，depth为1，size也为1，满足depth<=size，定理成立
如果e是一个Var，depth为1，size也为1，满足depth<=size，定理成立
若定理对e1和e2都成立，也就是e1和e2都分别满足depth e1<=size e1，depth e2<=size e2，那么对于由e1和e2由Plus进行构造的新元素e3，其depth=max(depth e1 e2)+1，size=size e1+size e2+1, 因此e3的depth是小于size的, 定理成立。
若定理对e1和e2都成立，也就是e1和e2都分别满足depth e1<=size e1，depth e2<=size e2，那么对于由e1和e2由Times进行构造的新元素e3，其depth=max(depth e1 e2)+1，size=size e1+size e2+1, 因此e3的depth是小于size的, 定理成立。

对应的Coq代码：

(* Our first proof!
   * Size is an upper bound on depth. *)
  Theorem depth_le_size : forall e, depth e <= size e.
  Proof.
    (* Within a proof, we apply commands called *tactics*.
     * Here's our first one.
     * Throughout the book's Coq code, we give a brief note documenting each tactic,
     * after its first use.
     * Keep in mind that the best way to understand what's going on
     * is to run the proof script for yourself, inspecting intermediate states! *)
    induct e.
    (* [induct x]: where [x] is a variable in the theorem statement,
     *   structure the proof by induction on the structure of [x].
     *   You will get one generated subgoal per constructor in the
     *   inductive definition of [x].  (Indeed, it is required that 
     *   [x]'s type was introduced with [Inductive].) *)

    simplify.
    (* [simplify]: simplify throughout the goal, applying the definitions of
     *   recursive functions directly.  That is, when a subterm
     *   matches one of the [match] cases in a defining [Fixpoint],
     *   replace with the body of that case, then repeat. *)
    linear_arithmetic.
    (* [linear_arithmetic]: a complete decision procedure for linear arithmetic.
     *   Relevant formulas are essentially those built up from
     *   variables and constant natural numbers and integers
     *   using only addition, with equality and inequality
     *   comparisons on top.  (Multiplication by constants
     *   is supported, as a shorthand for repeated addition.) *)

    simplify.
    linear_arithmetic.

    simplify.
    linear_arithmetic.

  Qed.

作者在书中没有给证明的细节，因为作者认为检查证明是机器做的事而不是人做的，因此把证明细节都放在附带的coq源代码里了。作者说很多发表的文章也倾向于给这种简要的证明让读者自己去弄明白，实际上这样的证明可能经常存在逻辑错误，导致人们接受虚假的定理。出于这个原因，这本书单独提供用于机器检查的证明代码，而书中的章节则用来介绍概念、推理原则以及关键定理和引理的陈述。

2.4 可判定理论 Decidable Theories

但是，我们在做证明的时候确实需要填充所有的证明细节。最方便的例子之一是一个证明目标符合某个可判定的理论。在遵循可计算性理论的前提下，我们考虑一些决策问题，F通常是无限的公式集合，T是真公式的集合，它包含于 F，是F的子集，然后我们只考虑那些用有限的推理规则集能证明的。

决策问题是可判定的，当且仅当存在一个总是能终止的程序，当传入集合F里面的某个元素f作为输入时，当且仅当f也是集合T的元素时程序返回true。（可以简单理解为判别一个F里的元素是否包含在真公式子集T里面。）理论的可判定性很方便，因为只要我们的目标属于一个可判定理论的F集，我们就可以通过运行已经存在的判定程序去自动释放目标。

（1）一个常见的可判定理论是线性算术linear arithmetic，它的F集合由以下语法生成为φ（在由整数常量、变量和只使用加减法组成的公式的基础上进行相等、不相等和大小的比较以及合取运算）。

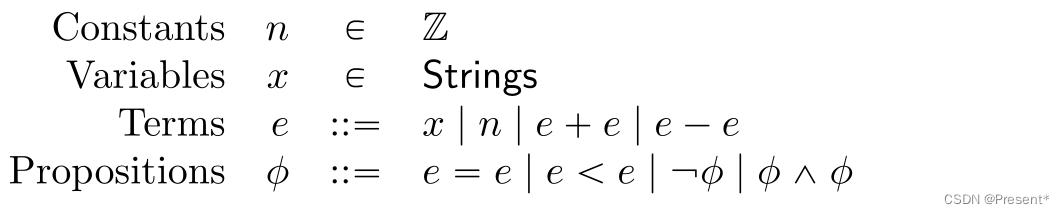
这里使用的算术术语与线性代数中的线性含义是相同的：也就是运算中只有加法和数乘，不出现平方等其他运算。但其实这里的语法定义把数乘都完全禁止了，不过我们在逻辑上允许用常数乘法作为重复加法的缩写。命题包含等式和小于检验，以及布尔否定(“not”)运算符和连接(“and”)运算符^。这组命题操作符就足以编码其他常见的不等式和命题操作符了。

在Coq这样的证明助手中使用可判定理论时，重要的是要理解一个理论如何应用于实际上不满足其语法的公式。作者举例说如果我们想证明f(x)-f(x)=0, 这里的f(x)可能是不同于上面的语法定义的其他奇奇怪怪的函数，但我们只需要引入一个新的变量y，并定义y=f(x)，我们就可以得到一个新的证明目标y-y=0。一个线性算术的程序可以很快地完成这个目标，然后我们可以再通过将y代回去推导出原始目标。在Coq里面，基于可判定理论的策略可以为我们完成以上所有的步骤。关键是我们一开始要能看出这个证明目标可以使用可判断理论。

（运用线性算术linear arithmetic的Coq代码示例见上一段Coq代码证明里用的linear_arithmetic策略。）

（2）另一个重要的可判定理论是带未解释函数的相等理论equality with uninterpreted functions (一个未解释的函数就是除了其名称和n元形式之外没有其他属性)。它的语法定义如下：

在这个理论里面，我们对所使用的变量或函数的详细属性一无所知，我们只能从判定相等的基本属性来进行推理:

自反性对称性传递性一致性

运用equality with uninterpreted functions的示例见如下Coq代码证明里用的equality策略：

  Theorem commuter_inverse : forall e, commuter (commuter e) = e.
  Proof.
    induct e; simplify; equality.
    (* [equality]: a complete decision procedure for the theory of equality
     *   and uninterpreted functions.  That is, the goal must follow
     *   from only reflexivity, symmetry, transitivity, and congruence
     *   of equality, including that functions really do behave as functions. *)
  Qed.

（3）还有可判定理论的另一个例子，algebraic structure of semirings半环的代数结构，它是类似于环但没有加法逆元的代数结构，它可能被称为“作用像自然数的类型”。

如果对于一个给定的x，存在一个x'使得x+x'=x'+x=0，则称x'是x的加法逆元

一个semiring半环是任何包含两个以0和1表示的元素的集合，在加法符号和乘法符号表示的二元运算下封闭。这里的符号0 1 + x都不是定死的，我们可以自由选择集合、元素和运算符，只要满足下面这些公理就行。

加法结合律：只要算子的位置没有改变，其运算的顺序就不会对结果有影响

加法幺元：当幺元和其他元素结合时，并不会改变那些元素

加法交换律：两个加数相加，交换加数的位置，和不变

乘法结合律

乘法幺元

乘法分配律：两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再将积相加

乘法零元：和其他数运算后还是0

（补充：逆元是运算后结果是单位元）

现在我们考虑只有满足以上这些公理得出的等式才是“正确的”，那么形式化的半环理论就是如下形式：

运用algebraic structure of semirings的示例见如下Coq代码证明里用的ring策略：

 Theorem commuter_constantFold : forall e, commuter (constantFold e) = constantFold (commuter e).

  Proof.
    induct e; simplify;
    repeat match goal with
           | [ |- context[match ?E with _ => _ end] ] => cases E; simplify
           | [ H : ?f _ = ?f _ |- _ ] => invert H
           | [ |- ?f _ = ?f _ ] => f_equal
           end; equality || linear_arithmetic || ring.
    (* [f_equal]: when the goal is an equality between two applications of
     *   the same function, switch to proving that the function arguments are
     *   pairwise equal.
     * [invert H]: replace hypothesis [H] with other facts that can be deduced
     *   from the structure of [H]'s statement.  This is admittedly a fuzzy
     *   description for now; we'll learn much more about the logic shortly!
     *   Here, what matters is that, when the hypothesis is an equality between
     *   two applications of a constructor of an inductive type, we learn that
     *   the arguments to the constructor must be pairwise equal.
     * [ring]: prove goals that are equalities over some registered ring or
     *   semiring, in the sense of algebra, where the goal follows solely from
     *   the axioms of that algebraic structure. *)

  Qed.

最后，半环理论的适用性和线性算术理论的适用性是不能比较的。因为有些目标可以用其中任意一种方法证明，而有些只能用半环理论证明，有些只能用线性算术理论证明。例如，通过半环理论，我们可以证明x(y+z)=xy+xz，而线性算术可以证明x-x=0。