【哈工大威海】模式识别总结

使用须知

动机：对我来说，整理这个笔记一方面是yq不敢出门，呆在家太闲了。另一方面，明年暑假，又或者12月可能会用到，其他专业课都打算整理下，现在前途未卜，只好做两手准备。
如果你是卷王，想直接看考试怎么考的，目录翻到最后，有我的考试回忆，不完全准确，仅供参考。
这个笔记是根据我备考整理的，比较适合对PPT已经比较熟悉的人。如果直接拿这个学，也不是不可以，但应该会比较吃力。此外，里面有一些自己的理解，可能不准确，欢迎探讨。
总的来说可以分成四部分
第1部分 第1讲 划水摸鱼
第2部分 第2-7讲 距离和线性分类器
第3部分 第8-13讲 概率论相关
第4部分 第14-15讲 划水摸鱼

复习笔记

第一讲 绪论

没啥好说的，没考。PPT主要是模式识别要学啥，祖师爷是谁，有哪些顶级会议、期刊，丁老师的经历。了解即可。

第二讲 距离分类器

一般形式和预备知识

1. $l-p$范数
   $\sqrt[p]{{\sum }_{i=1}^n{x}_i^p}$
2. 相似度与距离的负相关关系
   $S(x,\mu )=-d(x,\mu )$

最近邻分类器

原理

大二下的机器学习都学过了，不再赘述。

优缺点

1. 训练样本数量较多时效果良好
2. 计算量大(需要同所有训练样本计算距离)
3. 占用存储空间大(需要保存所有的训练样本)
4. 易受样本噪声影响

改进：模板匹配

选择模板，即每个类别构造出一个代表${\mu }_i$，即求解如下式子，$R^d$是d维特征空间，$d\left({\mathbf{x}}_k^{(i)},\mu \right)$用的欧氏距离。
${\mu }_i=\underset{\mu \in R^d}{\mathrm{argmin}}{\sum }_{k=1}^{n_i}d\left({\mathbf{x}}_k^{(i)},\mu \right)$
接下来求${\mu }_i$,误差平方和作为准则函数
$J_i(\mu )=\sum _{k=1}^{n_i}{\Vert {\mathbf{x}}_k^{(i)}-\mu \Vert }^2=\sum _{k=1}^{n_i}{\left({\mathbf{x}}_k^{(i)}-\mu \right)}^t\left({\mathbf{x}}_k^{(i)}-\mu \right)$
求导
$\nabla J_i(\mu )=\frac{\partial J_i(\mu )}{\partial \mu }={\sum }_{k=1}^{n_i}2\left({\mathbf{x}}_k^{(i)}-\mu \right)(-1)=2n_i\mu -2{\sum }_{k=1}^{n_i}{\mathbf{x}}_k^{(i)}=0$
其中用到了公式
$\frac{\partial ||\text{x}|{|}_2^2}{\partial \text{x}}=\frac{\partial ||{\text{x}}^T\text{x}|{|}_2}{\partial \text{x}}=2\text{x}$
最终解得
${\mu }_i=\frac{1}{n_i}{\sum }_{k=1}^{n_i}{\text{x}}_k^{(i)}$
结论：每个类别训练样本的均值作为匹配模板

衍生：多模板匹配

一个类别可以有多个模板，具体看PPT，理解就行
核心：$j=\underset{1\le i\le c}{\mathrm{argmin}}\left[\underset{1\le k\le m_i}{\min }(\mathbf{x},{\mathbf{\mu }}_i^k)\right]$，总共$c$类，第$i$类有$m_i$个模板。

K-近邻分类器

原理

大二下的机器学习都学过了，核心$j=\underset{1\le i\le c}{\mathrm{argmax}}{k}_i$。提下k的取值：

1. 过小：算法的性能接近于最近邻分类
2. 过大：距离较远的样本也会对分类结果产生作用，引起分类误差
3. 适合的K值需要根据具体问题来确定
   对于非平衡样本集，样本数多的类别总是占优势

优缺点

优点

1. 易于理解和实现
2. 训练时间短，有用的测试工具
3. 容易处理多分类
4. 非参数化
   缺点
5. 测试阶段的计算成本高
6. 易受数据分布的影响
7. 高维数据会降低 KNN 的精度

K-D树

K-D树用来解决计算成本的问题。

1. 一维特征
   退化为排序查找问题，快排+折半查找
2. 多维特征
   建树算法
   （1) 计算得到方差最大的第s维特征
   （2) 根据第s维特征，对D升排序
   （3) 选择中间样本为根节点、记录s，小于根节点放入左子集DL，大于根节点放入右子集DR
   （4) DL、DR递归建树，得到K-D树
   例子
   
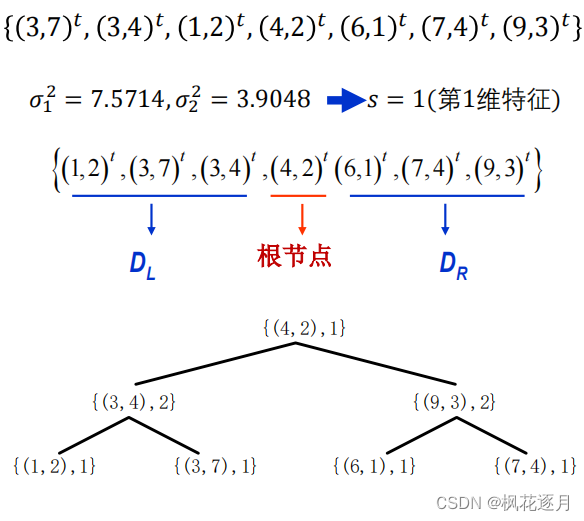
   用深度优先搜索找最近的点（样本）
   
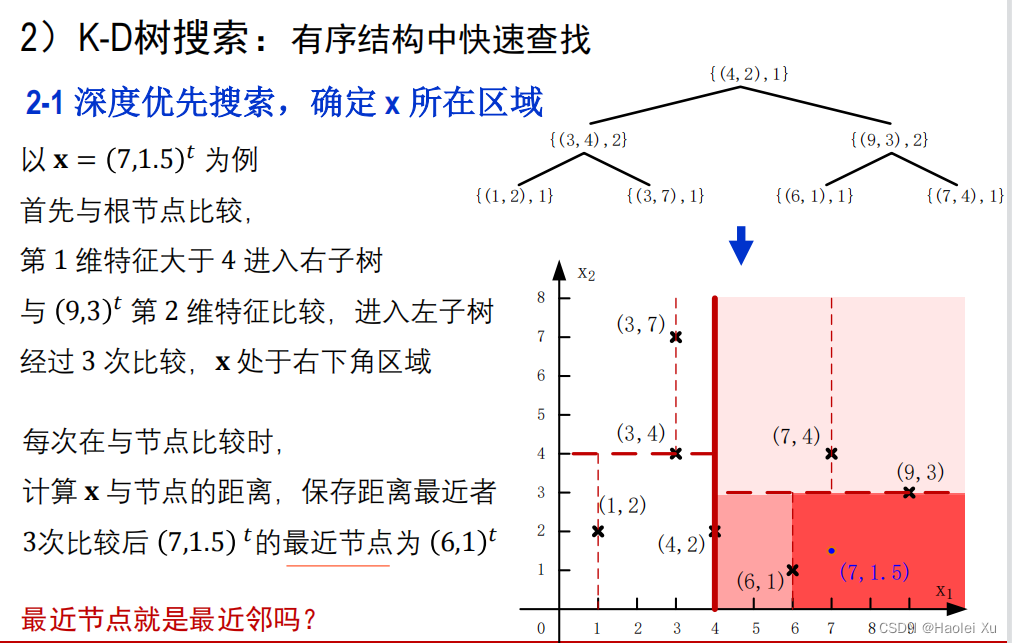
   进行检验，回溯搜索
   
   
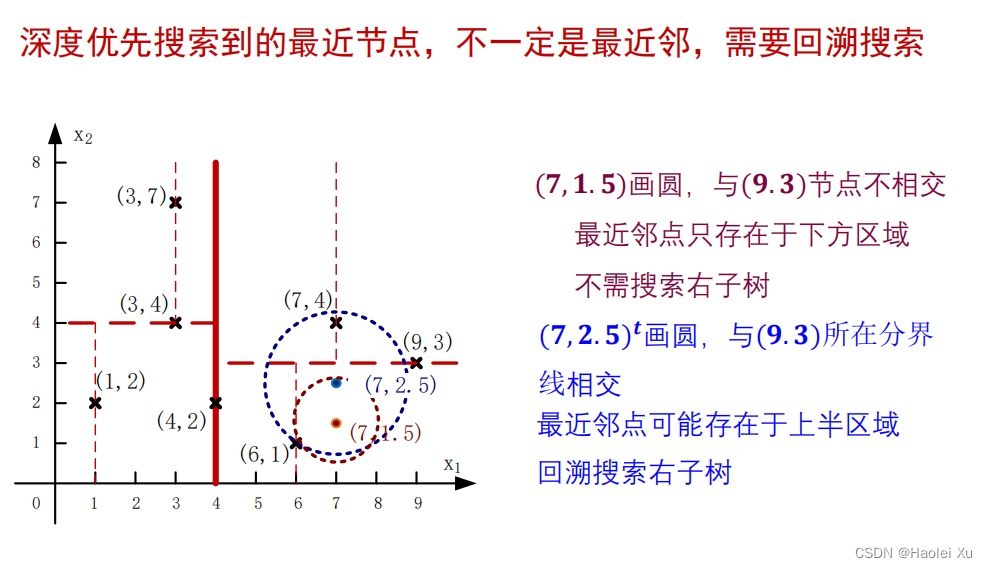
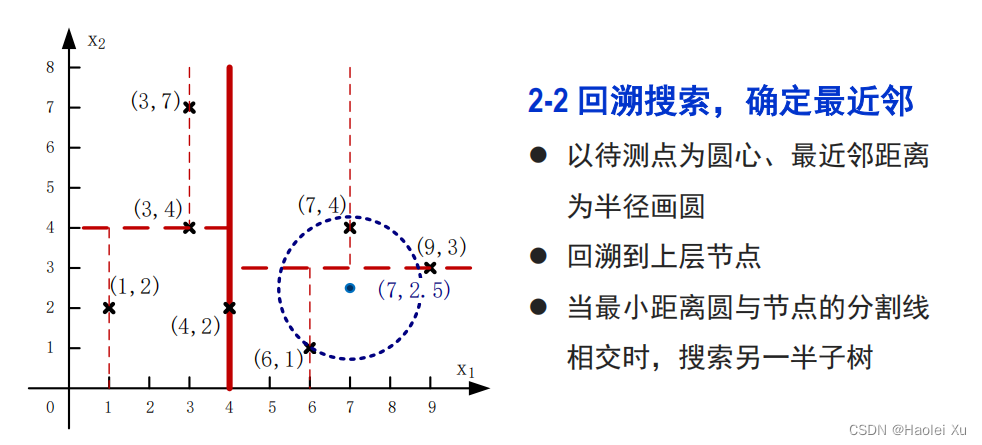
   再往上回溯时不会与（4，2）所在分界线相交了，停止搜索，算法结束。

距离和相似度度量

满足以下4个性质即可作为距离

1. 非负性：$d(\text{x},\text{y})\ge 0$
2. 对称性：$d(\mathbf{x},\mathbf{y})=d(\mathbf{y},\mathbf{x})$
3. 自反性：$d(\text{x},\text{y})=0,$当且仅当$\text{x}=\text{y}$
4. 三角不等式：$d(\text{x},\text{y})\le d(\text{x},\text{z})+d(\text{z},\text{y})$

常见的距离

1. 欧式距离$d(\mathbf{x},\mathbf{y})=\Vert \mathbf{x}-\mathbf{y}{\Vert }_2$
2. 街市距离$d(\mathbf{x},\mathbf{y})=\Vert \mathbf{x}-\mathbf{y}{\Vert }_1={\sum }_{i=1}^n\left|x_i-y_i\right|$
3. 车比雪夫距离$d(\mathbf{x},\mathbf{y})=\Vert \mathbf{x}-\mathbf{y}{\Vert }_{\infty }=\underset{1\le i\le d}{\max }|x_i-y_i|$
4. 汉明距离$d(\mathbf{x},\mathbf{y})={\sum }_{j=1}^d{\left(x_j-y_j\right)}^2$(二值矢量)
5. 加权距离 不同距离赋不同权重

相似性度量
角度相似性
当两个样本之间的相似程度只与它们之间的夹角有关、与矢量的长度无关时，可以使用矢量夹角的余弦来度量相似性
$s(\mathbf{x},\mathbf{y})=\cos {\theta }_{\mathbf{x}\mathbf{y}}=\frac{{\mathbf{x}}^t\mathbf{y}}{\Vert \mathbf{x}\Vert \cdot \Vert \mathbf{y}\Vert }=\frac{{\sum }_{i=1}^d{x}_i{y}_i}{\sqrt{{\sum }_{i=1}^d{x}_i^2}\cdot \sqrt{{\sum }_{i=1}^d{y}_i^2}}$
（注：若特征已经归一化，分母为1，直接计算内积即可，归一化在后面讲）
相关系数
$s(\mathbf{x},\mathbf{y})=\frac{(\mathbf{x}-{\mu }_{\mathbf{x}}{)}^t(\mathbf{y}-{\mu }_{\mathbf{y}})}{\Vert \mathbf{x}-{\mu }_{\mathbf{x}}\Vert \cdot \Vert \mathbf{y}-{\mu }_{\mathbf{y}}\Vert }=\frac{{\sum }_{i=1}^d(x_i-{\mu }_{x_i})(y_i-{\mu }_{y_i})}{\sqrt{{\sum }_{i=1}^d(x_i-{\mu }_{x_i}{)}^2}\cdot \sqrt{{\sum }_{i=1}^d(y_i-{\mu }_{y_i}{)}^2}}$

特征归一化、标准化

均匀缩放

假设各维特征服从均匀分布
$x_{j\min }=\underset{1\le i\le n}{\min }{x}_{ij},x_{j\max }=\underset{1\le i\le n}{\max }{x}_{ij},j=1,\cdots ,d$
$x_{ij}^{\prime }=\frac{x_{ij}-x_j\text{min}}{x_j\text{max}-x_j\text{min}},i=1,\cdots ,n,j=1,\cdots ,d$

高斯缩放

假设各维特征服从高斯分布
${\mu }_j=\frac{1}{n}{\sum }_{i=1}^n{x}_{ij},s_j=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(x_{ij}-{\mu }_j\right)}^2},j=1,\cdots ,d$
$x_{ij}^{\prime }=\frac{x_{ij}-{\mu }_j}{s_j},i=1,\cdots ,n,j=1,\cdots ,d$

分类器评价

评价指标

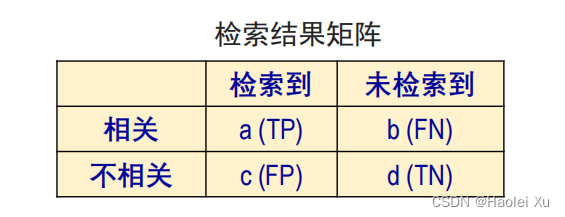
T：true，F：false，P：positive，N：negative
TP：真阳（识别正确，识别结果为阳性）
FN：假阴（识别错误，识别结果为阴性）实际应为阳性
FP：假阳（识别错误，识别结果为阳性）实际应为阴性
TN：真阴（识别正确，识别结果为阴性）
召回率： 多少阳性被找出来了
$Recall=\frac{TP}{TP+FN}=\frac{a}{a+b}$
查准率（精确率）： 找出来的阳的有多少是对的
$Precision=\frac{TP}{TP+FP}=\frac{a}{a+c}$
如何兼顾？

1. f1 score：即调和平均数
   $F_1=\frac{2}{\frac{1}{R}+\frac{1}{P}}=\frac{2RP}{R+P}=\frac{TP}{TP+\frac{FP+FN}{2}}$
2. $P-R$曲线

其他指标
敏感性$Se=\frac{a}{a+b}$，表示真正阳性能被检测出来的能力，就是召回率
特异性$Sp=\frac{d}{c+d}$，表示实际阴性不被误诊的能力，就是1-假阳率
两者结合有ROC曲线，了解

评价方法

1. 留出法
2. 交叉验证
3. 嵌套交叉验证
4. Bootstrap（有放回）
   偏差、方差、欠拟合、过拟合间的关系

第三讲 线性判别函数分类器（1）

线性判别函数和线性分类界面

线性判别函数

𝑑 维特征空间中的超平面方程
$H:g\left(\text{x}\right)={\text{w}}^t\text{x}+w_0=0$
超平面$H$的几何意义：

1. $g(x)>0$时，𝐱 处于 𝐻 上方 。$g(x)=0$时，𝐱 处于 𝐻 上 。$g(x)<0$时，𝐱 处于 𝐻 下方。
2. 权矢量𝐰垂直于分类面 𝐻，指向 $g(\mathbf{x})>0$ 的区域
3. 坐标原点到分类界面 𝐻 的距离：$r_0=\frac{{\text{w}}_0}{||\text{w}||}$
   性质1和3线性代数都学过。主要是性质2的证明。注意图中框出来的部分，应该理解前提，即$\overrightarrow{{\mathbf{x}}_p\mathbf{x}}$是根据$\overrightarrow{w}$的方向来构造的，在一开始就应该说明，PPT写的比较奇怪。
   

判别函数的学习

样本规范化与增广

直接看图，根据标签和偏置进行调整

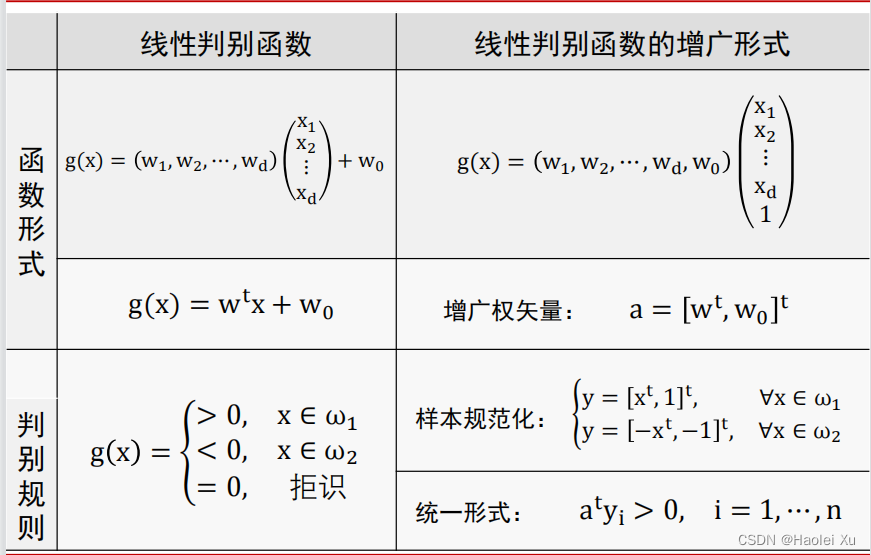
梯度下降算法

前置知识：导数、偏导、梯度、泰勒展开
准则函数的一阶近似
$\Delta \mathbf{a}$充分小，在 a 点附近可以用一阶展开式近似函数$\nabla J(\mathbf{a})$
$J(\mathbf{a}+\Delta \mathbf{a})\approx J(\mathbf{a})+\nabla J^t(\mathbf{a})\Delta \mathbf{a}$
学习率
也称为迭代步长，控制增量矢量 Δa 的长度
学习率过小，算法的收敛速度慢
学习率过大，算法有可能不收敛（振幅过大）
可以设置为常数，也可以设置为迭代次数 𝑘 的函数

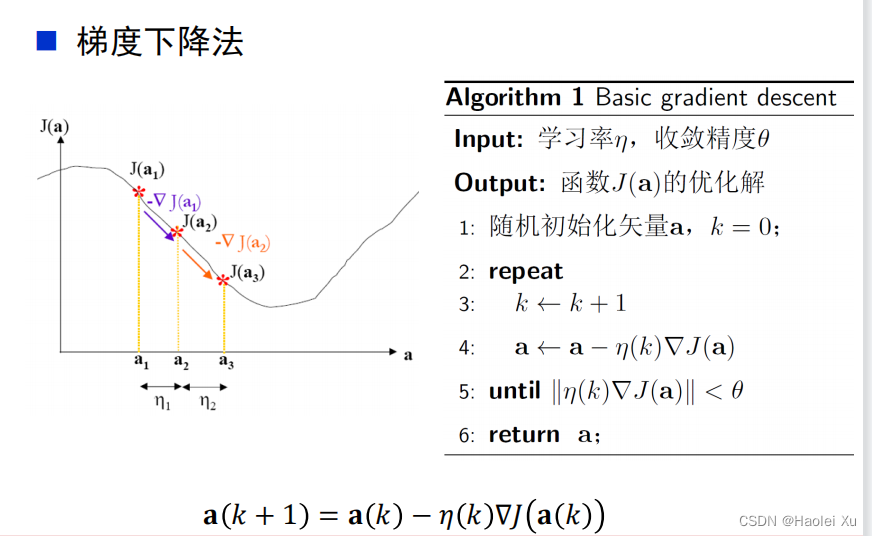
收敛性
对于一般的准则函数 𝐽(a)，梯度法只能收敛于局部的极值点，不能保证收敛于全局的最优点，与初始值的设置有关
二次准则函数具有唯一的极值点，梯度法可以保证收敛于最优解
所以一般得构造个凸函数

感知器算法

感知器算法的准则函数怎么选用？
第一种 直接以被错误分类的样本数量为准则优化
令 𝒴 为被判别函数错误分类的规范化增广训练样本集合
Y = { y i ∣ g ( y i ) ≤ 0 , i = 1 , ⋯   , n } \mathcal{Y}=\{\mathbf{y}_i|g(\mathbf{y}_i)\leq0,i=1,\cdots,n\} Y={yi​∣g(yi​)≤0,i=1,⋯,n}
$J_N(\mathbf{a})={\sum }_{\mathbf{y}\in \mathcal{Y}}1$
此方法问题较大

1. $J_N(\text{a})$是一个不连续函数，不连续点不可求导
2. 可以求导的区域，梯度为0，无法采用梯度法优化

第二种 以错误分类样本到判别界面“距离”之和作为准则
$J_P(\mathbf{a})={\sum }_{\mathbf{y}\in \mathcal{Y}}-g(\mathbf{y})={\sum }_{\mathbf{y}\in \mathcal{Y}}-{\mathbf{a}}^t\mathbf{y}$
样本规范化之后，被错误分类的训练样本 $g(y)<0$
当所有训练样本被正确识别时，$J_P(a)=0$，取得最小值
综上所述，这个准则函数是可以用梯度下降算法优化的
梯度为$\nabla J_P(\mathbf{a})=\sum _{\mathbf{y}\in \mathcal{Y}}-\mathbf{y}$
带入梯度下降公式的时候注意两个负号抵消了
例题
学会PPT上的例题即可，考试考了类似的题。




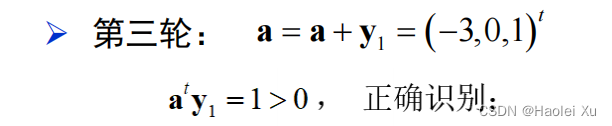
算出分类超平面后要会画图！

第四讲 线性判别函数分类器（2）

LSME算法

第三讲里面我们用的不等式来判断样本是否分对，第4讲改为等式。《最优化方法》这门课专门讲了下面这些东西，虽然是考查课，还是可以好好听听的，对数模等比赛都有帮助。
线性不等式组的求解可以转化为线性方程组的求解
$\{\begin{array}{l}{\mathbf{a}}^t{\mathbf{y}}_1>0\\ ⋮\\ {\mathbf{a}}^t{\mathbf{y}}_n>0\end{array}⟹\{\begin{array}{l}{\mathbf{a}}^t{\mathbf{y}}_1=b_1>0\\ ⋮\\ {\mathbf{a}}^t{\mathbf{y}}_n=b_n>0\end{array}$
注意上式都规范化了。
写成矩阵形式就是
$\left(\begin{array}{cccc}{y}_{10}& y_{11}& \cdots & y_{1d}\\ y_{20}& y_{21}& \cdots & y_{2d}\\ ⋮& ⋮& \ddots & ⋮\\ y_{n0}& y_{n1}& \cdots & y_{nd}\end{array}\right)\left(\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_d\end{array}\right)=\left(\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_n\end{array}\right)$
即$Ya=b,b>0$
一般来说这是一个超定方程组，只能求近似解。

1. 公式法
   定义误差矢量$e=Ya-b$
   定义准则函数（LSME）$J_S(a)=\Vert Ya-b{\Vert }^2={\sum }_{i=1}^n(a^t{y}_i-b_i{)}^2$
   目标是找到$a^{\ast }=\underset{a}{\mathrm{argmin}}{J}_S(a)$
   将LMSE准则函数展开：
   $J_S(\mathbf{a})=\Vert Y\mathbf{a}-\mathbf{b}{\Vert }^2={\left(Y\mathbf{a}-\mathbf{b}\right)}^t(Y\mathbf{a}-\mathbf{b})={\mathbf{a}}^t{Y}^{t}Y{\mathbf{a}-2\mathbf{b}}^{t}Y{\mathbf{a}+\mathbf{b}}^t\mathbf{b}$
   注意$2{\mathbf{b}}^{t}Y\mathbf{a}$是个1*1矩阵，动手推一下比啥都强
   求梯度和极值点
   $\frac{\partial J_S(\mathbf{a})}{\partial \mathbf{a}}=2Y^{t}Y\mathbf{a}-2Y^t\mathbf{b}=0$
   解得$\mathbf{a}={\left(Y^{t}Y\right)}^{-1}{Y}^t\mathbf{b}=Y^{+}\mathbf{b}$
   矩阵 $Y^{+}$称为伪逆矩阵
   所以最后就只要代个公式算一下，形式很简单，但是矩阵求逆计算量很大，考试时候丁老师会直接给逆矩阵，至少我们这届是。
   例题
   
   
   
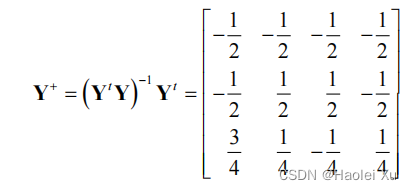
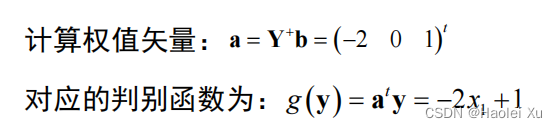
2. 梯度下降法
   既然刚才用公式法已经算出了梯度公式
   $\frac{\partial J_S(\mathbf{a})}{\partial \mathbf{a}}=2Y^{t}Y\mathbf{a}-2Y^t\mathbf{b}$
   那不妨代入梯度下降算法的迭代式，这对计算机来说友好的多
   

由线性到非线性

以上所有线性分类器都只适用于线性可分问题，无法解决非线性问题
著名的“异或问题”就无法解决
实现非线性分类的途径
广义线性判别函数（利用已有特征增加高次项，可能导致维数灾难）
分段线性判别函数（典型的有决策树）
多层感知器
核函数方法

多类别线性分类

以上讨论的都是二分类
接下来讨论三种多类别线性分类方法

一对多或一对一

这个考试考判别条件了

一对多

省流：c类需要c个分类面
每一类都有一个判别函数把自身和其他类区分开，第 i 类与其它类别之间的判别函数：$g_i(y)=a_i^{t}y$
准则：存在$i$使$g_i(x)>0,g_i(x)<0,j\ne i,$则判别$x$属于${\omega }_i$；如果不存在则拒识

一对一

省流：c类需要c(c-1)/2个分类面
第 i 类与第 j 类之间的判别函数为：$g_{ij}(y)=a_{ij}^{t}y,i\ne j$
准则：如果对任意$j\ne \mathrm{i}$，有$g_{ij}(x)>0$，则判别 $x$ 属于${\omega }_i$
一对一判别特例：最大值判别
每个类别构造一个判别函数：$g_i(y)=a_i^{t}y$
准则：$i=\underset{1\le j<c}{\mathrm{argmax}}{g}_j(\mathbf{x})$

拓展的感知机算法

基于上面的最大值判别，出现错分样本要同时修正多个权值矢量。

感知器网络

这个跟神经网络就很接近了
先说输出的编码方式，方法1类似onehot编码，方法2类似二进制编码

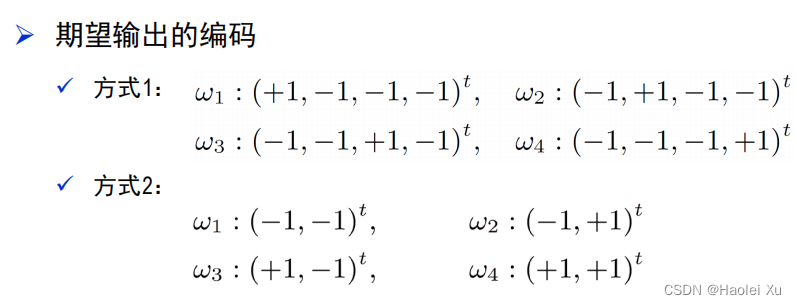
网络模型

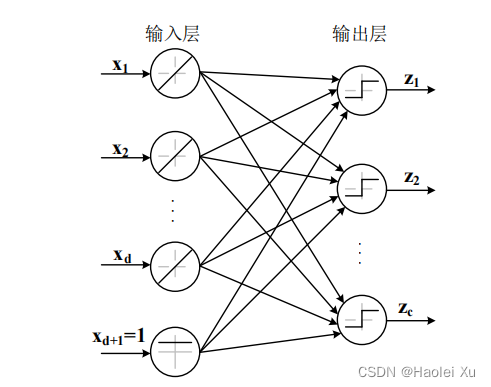
求解

第五讲 支持向量机

这部分明确说不考推导，就考了计算，一个小插曲是SVM的考题出错了，不过无伤大雅。功利点直接看例题，但是尝试理解推导很重要，如果《最优化方法》好好听的话会比较轻松，基本都讲过。

推导

推导过程

设分类面为$\begin{array}{r}g(\text{x})={\text{w}}^t\text{x}+w_0=0\end{array}$
函数间隔定义为$b_i=|g({\mathbf{x}}_i)|=|{\mathbf{w}}^t{\mathbf{x}}_i+w_0|$
几何间隔定义为${\gamma }_i=\frac{b_i}{\Vert \text{w}\Vert }$，说白了就是欧氏距离
支持向量和支持面的定义

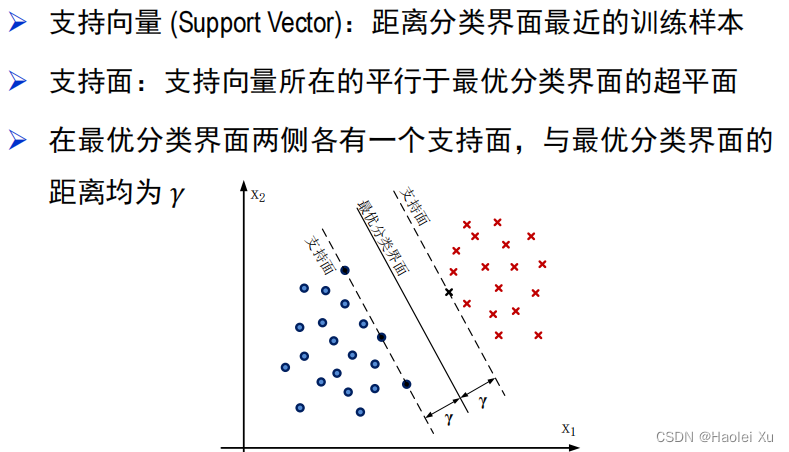
SVM的思想就是找到一个最优分类界面，即能够将线性可分样本集区分开的最大间隔超平面。说人话就是，使样本集到分类面的最小距离最大化。
定义完函数间隔、几何间隔后要做一个精彩操作：调整分类界面的函数间隔
当判别函数 $g(x)$ 能够正确区分训练样本时，有下式成立：
$z_i({\mathbf{w}}^t{\mathbf{x}}_i+w_0)\ge *{min}_{1\le j\le n}\left[z_j({\mathbf{w}}^t{\mathbf{x}}_j+w_0)\right]=b_{min}>0$
$z_i$是正负标签，这里没规范化
然后令$\text{w}\leftarrow \text{w/}{b}_{min},w_0\leftarrow w_0/b_{min}$
可以得到$z_i({\mathbf{w}}^t{\mathbf{x}}_i+w_0)\ge 1,i=1,\cdots ,n$
这个操作不会改变分类界面的位置，但可以将分类界面与样本集之间的函数间隔调整为 1。说人话就是把一个平面的表达式里的系数同比例放大或缩小。这个操作是为了减少变量方便后续推导和运算。
至此，问题转化为

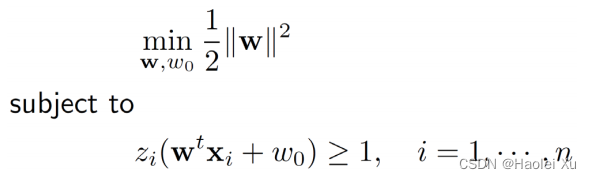
至于为什么要写成$\frac{1}{2}\Vert \mathbf{w}{\Vert }^2$，第三讲的笔记已经进行了说明，为了使得能够找到最优解，一般得整个凸函数，把问题转变为凸优化问题。
接下来用拉格朗日乘数法，高数学过，用来解决等式约束问题，但这里是不等式，多个KKT条件，KKT条件参考PPT。
$\text{L}(w,w_0,\alpha )=\frac{1}{2}\Vert w{\Vert }^2-{\sum }_{i=1}^n{\alpha }_i[z_i(w^t{x}_i+w_0)-1]$
根据KKT条件，${\alpha }_i\ge 0$
问题转换为求$\underset{w,w_0}{\min }\underset{\alpha }{\max }L(w,w_0,\alpha )$
该问题是强对偶问题（证明较难，了解），等价于求
$\underset{\alpha }{\max }\underset{w,w_0}{\min }L(w,w_0,\alpha )$
交换min和max的顺序后就可以先求解$w，w_0$。先看内层，即针对 $w，w_0$ 的最小值问题，分别对参数$w，w_0$ 求导，令导数为 0
$\frac{\partial \mathrm{L}(\mathrm{w},{\mathrm{w}}_0,\alpha )}{\partial \mathrm{w}}=\mathrm{w}-{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{z}}_{\mathrm{i}}{\alpha }_{\mathrm{i}}{\mathrm{x}}_{\mathrm{i}}=0$
$\frac{\partial \mathrm{L}(w,w_0,\alpha )}{\partial w_0}={\sum }_{\text{i}=1}^{\text{n}}{z}_{\text{i}}{\alpha }_{\text{i}}=0$
解得
$w={\sum }_{\mathrm{i}=1}^n{\mathrm{z}}_{\mathrm{i}}{\alpha }_{\mathrm{i}}{x}_{\mathrm{i}}(1)$
${\sum }_{\text{i}=1}^{\text{n}}{z}_{\text{i}}{\alpha }_{\text{i}}=0(2)$
这结论要记住，做题会用到
把$（1）（2）$两式代回$\text{L}(w,w_0,\alpha )$并化简，得到
$L(\mathbf{\alpha })=-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^n{\alpha }_i{\alpha }_j{z}_i{z}_j{\mathbf{x}}_i^t{\mathbf{x}}_j+{\sum }_{i=1}^n{\alpha }_i$
最后问题转化为

对偶问题的优点

做到这里可以发现转化为对偶问题的优点

1. 不直接优化权值矢量
   与样本的特征维数无关，只与样本的数量有关
   当样本的特征维数很高时，对偶问题更容易求解
2. 只用内积，不用坐标
   训练样本只以内积的形式出现
   优化求解过程中，只需计算内积

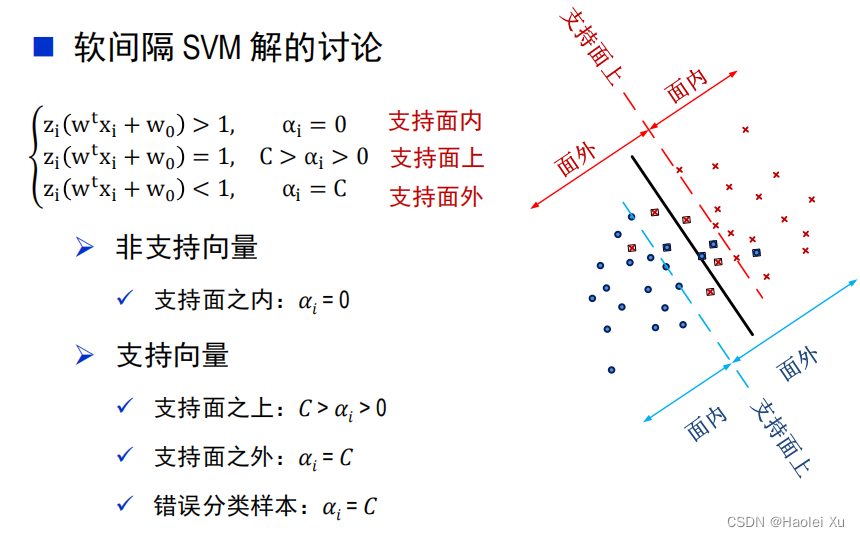
SVM解的讨论

事实上，样本里真正重要的是那些作为支持向量的样本。在拉格朗日乘数法中，只有支持向量的${\alpha }_i$才不为0，其他均为0。

例题

很简单，记住结论直接套公式

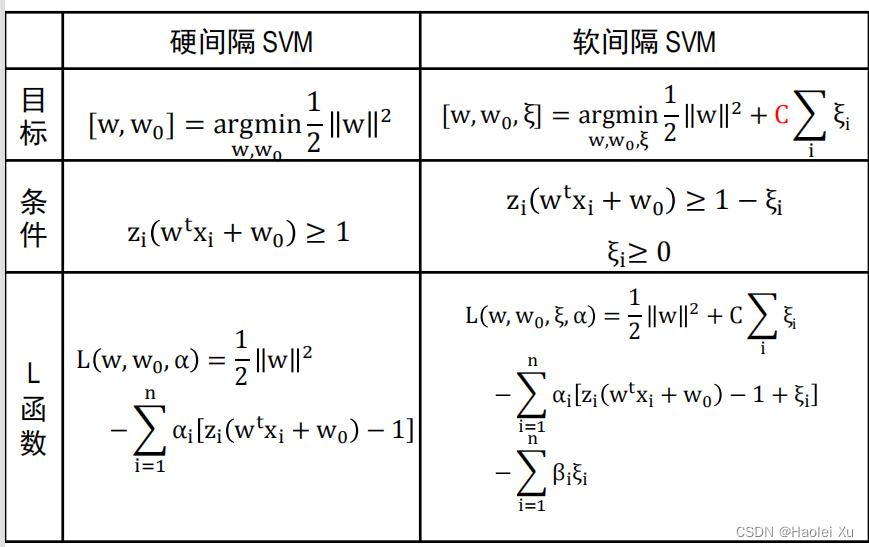
软间隔SVM

实际应用中，对于线性不可分的训练集，不等式约束不可能全部被满足（找不到解）。
于是引入了松弛变量${\xi }_i\ge 0$（每个样本对应一个松弛变量），将不等式约束变为
$z_i(w^{\mathrm{t}}{\mathrm{x}}_{\mathrm{i}}+w_0)\ge 1-{\xi }_{\mathrm{i}}$
只要选择一系列适合的松弛变量，不等式约束条件总是可以得到满足的。好的判别函数能够正确分类更多的样本，因此希望更多松弛变量满足${\xi }_i=0$。对于那些被错分的样本，引入惩罚系数$C$，于是软间隔SVM问题可以表述为

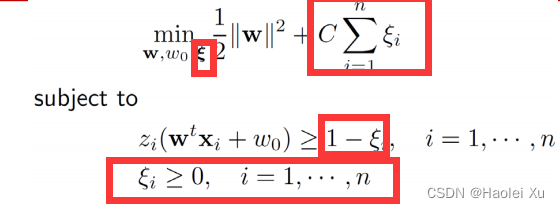
$C$越大，对错分的惩罚力度越大，$C$越小，获得的分类面间隔越大。

核函数

由来

第四讲提到了广义线性判别函数：将低维特征向量映射到高维空间中，学习线性判别函数。
根据已有的特征无法使用线性分类器，但可以根据已有特征构建高维特征，如建立非线性映射$\varphi :(x_1,x_2{)}^t\to (x_1^2,\sqrt{2}{x}_1{x}_2,x_2^2{)}^t$，下图经过转换后在三维空间就线性可分了。

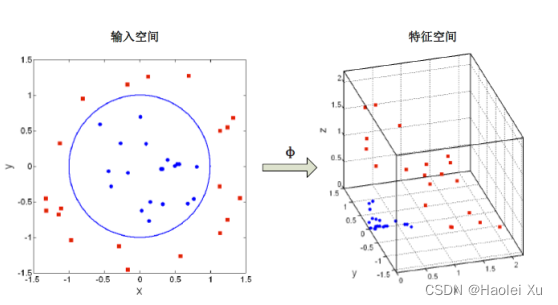
问题来了，如果采用这种非线性映射，我每个样本在输入训练时都得先带入函数$\varphi$进行转换。其计算复杂度与特征空间的维数$(D\gg d）$相关，可能引发维数灾难，当$D\to +\infty$，很难在特征空间中计算内积（原来是算x，y的内积，才d维，现在升维后整成D维的内积了）。
于是就引入了核函数（核技巧）。说实话就是化简了一下。比如刚才的非线性映射$\varphi :(x_1,x_2{)}^t\to (x_1^2,\sqrt{2}{x}_1{x}_2,x_2^2{)}^t$
$⟨\Phi (x),\Phi (y)⟩={\left(x_1^2,\sqrt{2}{x}_1{x}_2,x_2^2\right)}^{\text{t}}\left(y_1^2,\sqrt{2}{y}_1{y}_2,y_2^2\right)$
$={\mathrm{x}}_1^2{\mathrm{y}}_1^2+\sqrt{2}{\mathrm{x}}_1{\mathrm{x}}_2\sqrt{2}{\mathrm{y}}_1{\mathrm{y}}_2+{\mathrm{x}}_2^2{\mathrm{y}}_2^2=({\mathrm{x}}_1{\mathrm{y}}_1+{\mathrm{x}}_2{\mathrm{y}}_2{)}^2=⟨\mathrm{x},\mathrm{y}{⟩}^2$
$\varphi$对应的核函数就是$K(x,y)=(x^{t}y{)}^2=⟨x,y{⟩}^2$
若不采用核函数需要计算$<\varphi (x),\varphi (z)>$这么个D维的内积，现在不用了，还是像升维之前那样先计算d维的内积，把内积结果再丢到核函数$K$进行计算，两种算法等价，但计算量显著下降。

核函数需要满足的条件

Mercer 条件，了解

常用的核函数

RBF（又称高斯核）
Poly
Sigmoid

带核技巧的SVM

引入非线性后，SVM要强大得多。

第六讲 特征选择与特征提取（1）

刚才的核技巧是升维，但是有时候特征过多并不是好事。可能导致

1. 增大了分类学习过程和识别过程计算和存储的复杂程度
2. 降低了分类器的效率
3. 识别特征维数过大使得分类器过于复杂

这一讲主要是选择特征
好的特征应当使得不同类别之间差异大（距离远），同一类别之间差异小（距离近）

类别可分性判据

基于距离的可分性判据

类内距离准则

用每个样本与其所属类别中心之间的距离平方和来度量
$J_W(C_1,\cdots ,C_k)=\frac{1}{n}{\sum }_{j=1}^k{\sum }_{x\in C_j}{\Vert x-{\mathrm{m}}_j\Vert }^2$
${\text{m}}_{\text{j}}=\frac{1}{n_j}{\sum }_{x\in C_j}\text{x}$

类间距离准则

用每个类别的中心到样本整体中心之间的加权距离平方和度量
$J_B(C_1,\cdots ,C_k)={\sum }_{j=1}^k\frac{n_j}{n}{\Vert {\text{m}}_{\text{j}}-\text{m}\Vert }^2$
$\text{m}=\frac{1}{n}{\sum }_{x\in D}x$

基于散布矩阵的可分性判据

第 j 类内散布矩阵
$S_W^j=\frac{1}{n_j}{\sum }_{x\in C_j}(x-m_j)(x-m_j{)}^t$
总的类内散布矩阵
$S_W=\sum _{j=1}^k\frac{n_j}{n}{S}_W^j$
类间散布矩阵
$S_{\mathbf{B}}={\sum }_{j=1}^k\frac{n_j}{n}(m_{\mathbf{j}}-\mathbf{m})(m_{\mathbf{j}}-\mathbf{m}{)}^t$
总体散布矩阵
$S_{\mathrm{T}}=\sum _{x\in D}\frac{1}{n}(x-m)(x-m{)}^t=S_{\mathrm{w}}+S_{\mathrm{B}}$
基于上述矩阵，一般有如下判据，值越大说明特征越好
$J_1(X)=tr\left(S_W^{-1}{S}_{\text{B}}\right)$
$J_2(X)=\frac{tr(S_{\text{B}})}{tr(S_{\text{W}})}$
$J_3(X)=\frac{|S_B|}{|S_W|}=\left|S_W^{-1}{S}_B\right|$
$J_4(X)=\frac{|S_{\text{T}}|}{|S_{\text{W}}|}$
tr是矩阵的迹，对角线之和，忘了可以翻翻线性代数课本。

例题

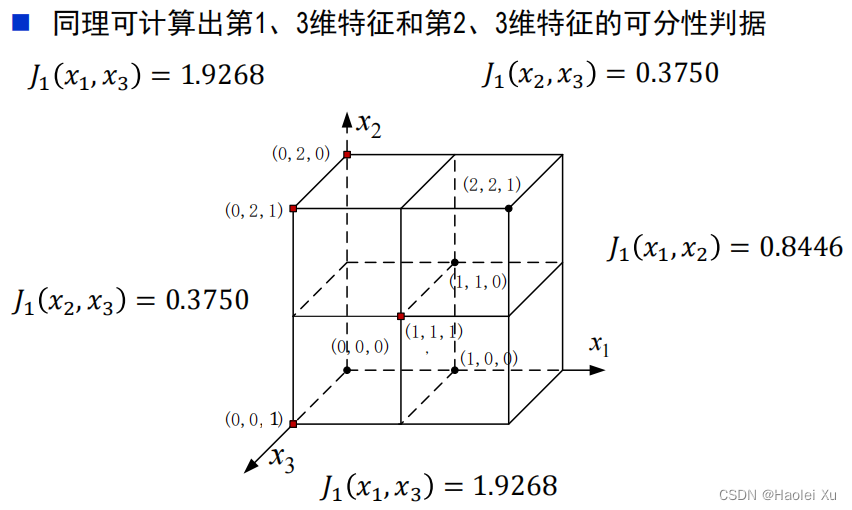
特征选择

分支定界法

上面的例题一共给了三个特征，要选出最好的两个，这样就有$C_3^2$种选择。如果从100个特征中选择10个时，组合数则变为$C_{100}^{10}=17310309456440$，显然难以计算。
当判据满足单调性时（加入新的特征后至少判据值不会更小），可以构建搜索树来选择特征。
例题



需要注意

1. 可分性判据必须具有单调性，否则不能保证得到最优选择
2. 最优解分支位置决定计算复杂度（看脸，脸好就快）
3. 当原始的特征维数很大时，搜索到最优解的计算量仍可观

次优搜索算法

思想类似局部最优，具体看ppt，了解算法和计算量就行。

1. 顺序前进法
2. 顺序后退法
3. 广义顺序前进（后退）法
4. 增 𝑙 – 减 𝑟 法（𝑙−𝑟法）

第七讲 特征选择与特征提取（2）

这部分老师说了不考推导，考试考了两个算法的区别

PCA

思想

建立新的坐标系，用更少的坐标重新表示数据，理想情况下，新的坐标表示可以完美地恢复数据
推导比较复杂，建议看PPT

算法

就考试来说，特征值是要会算的，忘了就去看线性代数课本。协方差矩阵会给。

例题

解的讨论

特征值描述了变换后各维特征的重要性，特征值为 0 的各维特征为冗余特征
PCA降维后各特征是不相关的（正交，独立）
PCA是无监督的，可以看到整个计算过程不需要样本标签值

LDA

Fisher 线性判别准则的思想

算法

要用到上一讲的散布矩阵，PPT这一讲给的的散布矩阵有点不一样，没取均值，不影响特征值计算。

解的讨论

与PCA不同，降维后的特征非正交
有监督，需要标签（散布矩阵那边）
新的坐标至多c-1维（c为类别数），即$S_W^{-1}{S}_b$ 至多存在 c-1 个大于 0 的特征值

其他方法

了解
PCA 与 LDA 的结合
LDA 作为线性分类器学习方法
PCA 的神经网络实现：AE（Auto-Encoder）
统计学方法

1. 独立成分分析 ( ICA, Independent Component Analysis )
2. 多维尺度变换 (MDS, Multidimensional Scaling)
3. 典型相关分析 (CCA, Canonical Correlation Analysis)
4. 偏最小二乘 (PLS, Partial Least Square)
   核方法
5. 引入核函数，将线性方法推广为非线性方法
   流形学习（Manifold Learning）
6. “非线性流形”在局部用“线性流形”近似，如 Isomap 和 Locally Linear Embedding（LLE）

第八讲 贝叶斯决策理论

从这里开始就都是概率论的东西了，开始新篇章。

概率论与统计学习

先复习下概率论
类别的先验概率 $P({\omega }_i),i=1,...,c$
后验概率 $P({\omega }_i|\mathbf{x})$
类条件概率密度（似然）$p(\mathbf{x}|{\omega }_i)$
样本的先验概率密度 $P(x)$
联合概率 $p(\mathbf{x},{\omega }_i)$
联合概率公式
$p(\mathbf{x},{\omega }_i)=P({\omega }_i|\mathbf{x})p(\mathbf{x})=p(\mathbf{x}|{\omega }_i)P({\omega }_i)$
全概率公式
$p(\mathbf{x})={\sum }_{i=1}^{c}p(\mathbf{x},{\omega }_i)={\sum }_{i=1}^{c}p(\mathbf{x}|{\omega }_i)P({\omega }_i)$
贝叶斯公式
$P({\omega }_i|\mathbf{x})=\frac{p(\mathbf{x}|{\omega }_i)P({\omega }_i)}{p(\mathbf{x})}$
例题


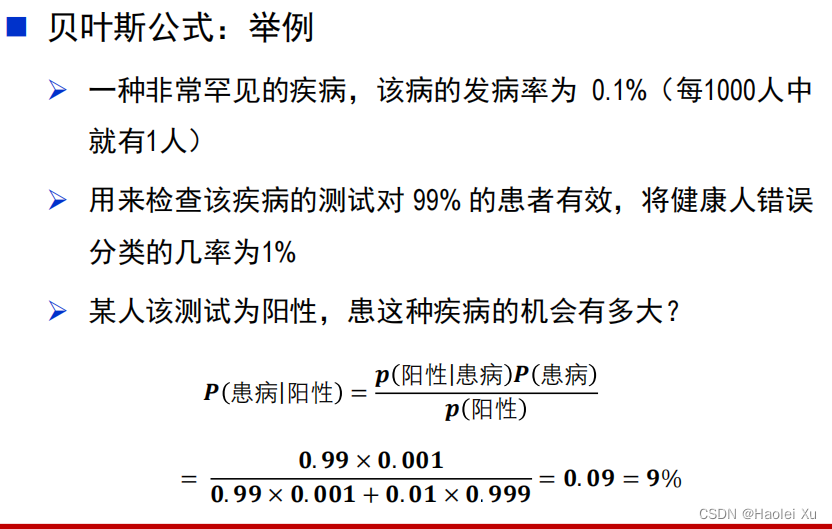
注意两次的区别，第一次的计算直接改变了第二次的先验概率。

贝叶斯决策理论

直接看题吧，不是什么新东西，最小风险稍微注意下

基于最小错误率的贝叶斯决策

算出来不患癌症，跟常识不符合，故引入风险。

基于最小风险的贝叶斯决策

${\lambda }_{ij}$表示把第i类识别成j类的风险。如果i和j相等，也就是识别对了，那当然没有风险，直接设为0，计算时忽略。
例题的${\lambda }_{12}$表示把第1类识别成2类的风险，即把癌症识别成正常人，漏诊了，要出人命肯定不行，风险设大一点为100。反过来把正常人识别成癌症要好不少，虚惊一场不出人命，风险设小一点为25。这样算出来是符合常识的。

第九讲 正态分布的贝叶斯分类器

贝叶斯分类器最重要的无疑是类条件概率密度函数，光靠统计比较困难，处理连续类的问题也比较困难。

判别函数和判别边界

判别函数的性质

判别函数不是唯一的
如果 { g i ( x ) } \{g_i(\textbf{x})\} {gi​(x)}是一组判别函数，$i=1,...,c$
对于任意的$\alpha >0$， { α g i ( x ) } \{\alpha g_i(\textbf{x})\} {αgi​(x)}是一组等价的判别函数
对于任意的$C\in R$，$g_i(\text{x})+C$ 是一组等价的判别函数
对于单调上升函数$f(\cdot )$， { f ( g i ( x ) ) } \{f\big(g_i(\mathbf{x})\big)\} {f(gi​(x))}是一组等价的判别函数
等价的判别函数具有相同的决策区域和判别边界

判别边界

判别区域之间的边界称为判别边界，在判别边界上相邻的两个判别函数值相等

正态分布贝叶斯

预备知识

一维正态分布
$p(x)\sim N(\mu ,{\sigma }^2)p(x)=\frac{1}{\sqrt{2\pi }\sigma }exp\left[-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2\right]$
多维正态分布
$p(\mathbf{x})\sim N(\mathbf{\mu },\mathbf{\Sigma })$
$p(\mathbf{x})=\frac{1}{{(2\pi )}^{d/2}|\mathbf{\Sigma }{|}^{1/2}}exp\left[-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^t{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathbf{\mu })\right]$
其中
均值矢量$\mu \approx \frac{1}{n}{\sum }_{i=1}^n{\text{x}}_i$
协方差矩阵$\Sigma \approx \frac{1}{n}{\sum }_{i=1}^n({\mathbf{x}}_i-\mu )({\mathbf{x}}_i-\mu {)}^t$
最大熵定理：在均值、方差确定的各种分布中，正态分布的熵最大
中心极限定理：大量小的、独立随机分布的总和等效为正态分布

推导

根据判别函数的性质
最小错误率贝叶斯判别函数的对数表示为
$g_i(\mathbf{x})=\ln p\left(\mathbf{x}|{\omega }_i\right)+\ln P\left({\omega }_i\right)$
假设类条件概念概率函数满足正态分布
$p\left(\mathbf{x}|{\omega }_i\right)=\frac{1}{{(2\pi )}^{d/2}|\mathbf{\Sigma }{|}^{1/2}}exp\left[-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^t{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathbf{\mu })\right]$
故有
$g_i(\mathbf{x})=-\frac{1}{2}{\left(\mathbf{x}-{\mu }_i\right)}^t{\mathbf{\Sigma }}_i^{-1}(\mathbf{x}-{\mu }_i)-\frac{d}{2}\ln 2\pi -\frac{1}{2}\ln \left|{\mathbf{\Sigma }}_i\right|+\ln P\left({\omega }_i\right)$
（其中，$\frac{d}{2}\ln 2\pi$是与类别无关的常数项，可以省略）

情况一

各类别的先验概率相同（常数）：$P({\omega }_i)=1/c$
各类别的协方差矩阵相同，且各向同性（常数）：${\mathbf{\Sigma }}_i={\sigma }^2\text{I}$ ($\text{I}$是单位矩阵)
化简并去掉常数项

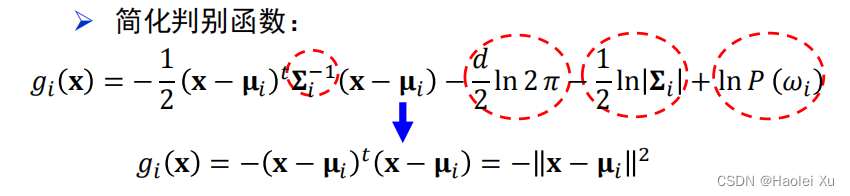
此时退化成为***距离分类器***

情况二

各类别的协方差矩阵相同，但非各向同性
${\Sigma }_i=\mathbf{\Sigma }$


这种情况等价于***线性分类器***$g_i(\mathbf{x})={\mathbf{w}}_i^t\mathbf{x}+w_{i0}$
其中
权重${\mathbf{w}}_i={\mathbf{\Sigma }}^{-1}{\mathbf{\mu }}_i$
偏置$w_{i0}=-\frac{1}{2}{\mathbf{\mu }}_i^t{\mathbf{\Sigma }}^{-1}{\mathbf{\mu }}_i+\ln P({\omega }_i)$

情况三

${\Sigma }_i$任意
$\frac{d}{2}\ln 2\pi$是与类别无关的常数项，可以省略，故有

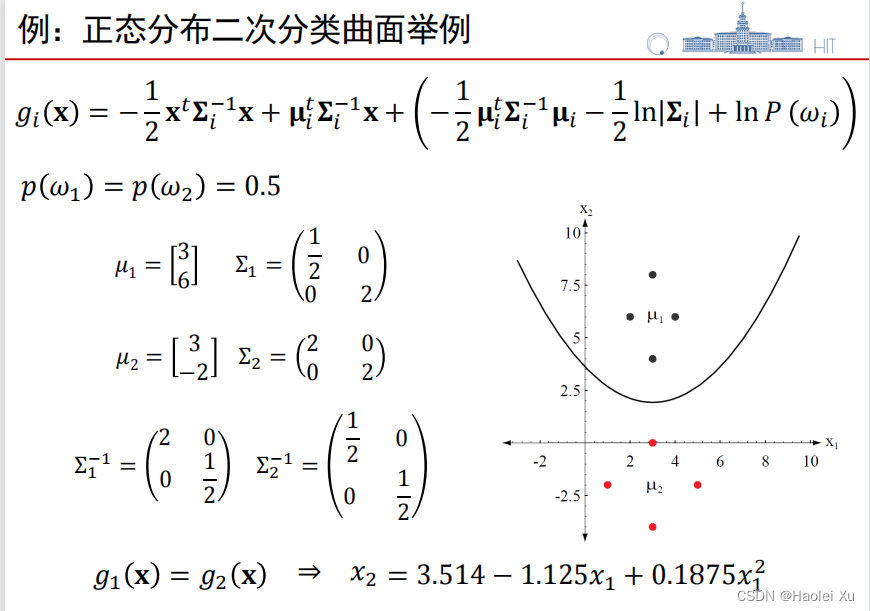
结果为***二次曲面***
求判别边界例题

朴素贝叶斯分类器

协方差矩阵经常很难估计
特征的维数较高、训练样本数量较少时，无法有效估计协方差矩阵
假设各维特征独立且服从相互独立的高斯分布
根据概率论知识就可以拆成各个独立特征的乘积
$p(\mathbf{x}|{\omega }_i)=\prod _{j=1}^{d}p(x_j|{\omega }_i)=\prod _{j=1}^d\left\{\frac{1}{\sqrt{2\pi }{\sigma }_{ij}}\exp \left[-\frac{(x_j-{\mu }_{ij}{)}^2}{2{\sigma }_{ij}^2}\right]\right\}$
取对数并化简，删掉常数项，得
$g_i(\mathbf{x})=\ln P\left({\omega }_i\right)-{\sum }_{j=1}^d\ln {\sigma }_{ij}-{\sum }_{j=1}^d\frac{{\left(x_j-{\mu }_{ij}\right)}^2}{2{\sigma }_{ij}^2}$
改进二次判别函数（MQDF）了解，不考

第十讲 非参数估计和参数估计

独立同分布假设
训练集 $D$ 中的样本抽样自同一分布， { x 1 , … , x n } ∼ p ( x ) \{\textbf{x}_1,\ldots,\textbf{x}_n\}\sim p(\textbf{x}) {x1​,…,xn​}∼p(x)
每个样本的抽样过程是相互独立的
独立同分布假设是统计学的一个基本假设

非参数估计

非参数估计的一般性描述

不需要任何关于分布的先验知识，适用性好
取得准确的估计结果，需要的训练样本数量远多于参数估计方法
令 $R$ 是包含样本点 $\mathbf{x}$ 的一个区域，体积为 $V$；$n$ 个训练样本中有 $k$ 个落在区域 $R$ 中，可对 $\mathbf{x}$ 的概率密度作出估计$\begin{array}{r}p(\text{x})\approx \frac{k/n}{V}\end{array}$

Parzen 窗法

Parzen 窗法估计的是每个类别的条件概率

定义

这个就是《信号处理》里的东西
Parzen 窗法使用窗函数来划定区域 $R$
以$x$为中心，边长为$h_n$的窗函数
$\phi \left(\frac{\text{u}-\text{x}}{h_n}\right)=\{\begin{array}{llc}1,& |u_i-x_i|\le \frac{h_n}{2},& i=1,\cdots ,d\\ 0,& otherwise& \end{array}$
判断样本$x_i$是否在超立方体$R$之内
$\phi \left(\frac{{\text{x}}_i-\text{x}}{h_n}\right)=\{\begin{array}{l}1,{\text{x}}_i\in R\\ 0,{\text{x}}_i\notin R\end{array}$
超立方体内的样本数
$k_n={\sum }_{i=1}^n\phi \left(\frac{\text{x}-{\text{x}}_i}{h_n}\right)$
代入求概率密度函数
$p(\text{x})\approx \frac{k/n}{V}$
$p(\text{x})=\frac{1}{n}{\sum }_{i=1}^n\frac{1}{V_n}\phi \left(\frac{\text{x}-{\text{x}}_i}{h_n}\right)$

算法

近邻分类器

定义

近邻法估计的是每个类别的后验概率
构造一个以待识别模式 $\mathbf{x}$ 为中心的区域 $R$，体积为 $V$
${\omega }_i$ 类联合概率的估计：
$p(\mathbf{x},{\omega }_i)\approx \frac{k_i/n}{V}$
${\omega }_i$ 类后验概率的估计:
$P({\omega }_i|\mathbf{x})=\frac{p(\mathbf{x},{\omega }_i)}{p(\mathbf{x})}=\frac{p(\mathbf{x},{\omega }_i)}{{\sum }_{j=1}^{c}p(\mathbf{x},{\omega }_j)}\approx \frac{k_i}{{\sum }_{j=1}^c{k}_j}=\frac{k_i}{k}$

算法

参数估计

参数估计方法需要关于分布形式的先验知识，估计的准确程度依赖于先验知识是否准确
由于有先验知识的存在，参数估计方法使用比较少的训练数据就可以得到较好的估计结果

最大似然估计

考试考了计算，建议翻看概率论课本找找例题

一维正态分布的最大似然估计

$p(x)=\frac{1}{\sqrt{2\pi }\sigma }exp\left[-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2\right]$
构造对数似然函数：
$l(\mu ,{\sigma }^2)={\sum }_{i=1}^n\ln p(x_i|\mu ,{\sigma }^2)={\sum }_{i=1}^n-\frac{1}{2}\left[\ln 2\pi +\ln {\sigma }^2+\frac{(x_i-\mu {)}^2}{{\sigma }^2}\right]$
计算偏导数：
$\frac{\partial l}{\partial \mu }={\sum }_{i=1}^n\frac{1}{{\sigma }^2}(x_i-\mu )$
$\frac{\partial l}{\partial {\sigma }^2}={\sum }_{i=1}^n\left[-\frac{1}{2{\sigma }^2}+\frac{(x_i-\mu {)}^2}{2{\sigma }^4}\right]$
求解
$\frac{1}{{\hat{\sigma }}^2}\sum _{i=1}^n\left(x_i-\hat{\mu }\right)=0$
$-\frac{n}{{\hat{\sigma }}^2}+\frac{1}{{\hat{\sigma }}^4}{\sum }_{i=1}^n(x_i-\hat{\mu }{)}^2=0$
解得
$\hat{\mu }=\frac{1}{n}{\sum }_{i=1}^n{x}_i$
${\hat{\sigma }}^2=\frac{1}{n}{\sum }_{i=1}^n{\left(x_i-\hat{\mu }\right)}^2$

多维正态分布的最大似然估计

推导跟上面类似，变成矩阵而已。
结论
$\hat{\mathbf{\mu }}=\frac{1}{n}{\sum }_{i=1}^n{\mathbf{x}}_i$
$\hat{\mathbf{\Sigma }}=\frac{1}{n}{\sum }_{\text{i}=1}^n({\mathbf{x}}_{\text{i}}-\hat{\mathbf{\mu }})({\mathbf{x}}_{\text{i}}-\hat{\mathbf{\mu }}{)}^{\text{t}}$

贝叶斯估计

没讲，愉快略过hhh

第十一讲 高斯混合模型

介绍

刚才的最大似然估计需要训练数据符合何种分布的先验知识，得先知道分布类型才能算参数
实际应用中一般不知道分布类型，GMM 可以看作是一种“通用”的概率密度函数，只要数量 𝑀 足够大，GMM 可以任意精度逼近任意分布密度函数
说人话，假设样本A、B来源于$p_1$这个正态分布，样本C、D来源于$p_2$这个正态分布，ABCD又是同一类标签，GMM要做的就是把这两个正态分布以加权的形式统一起来。
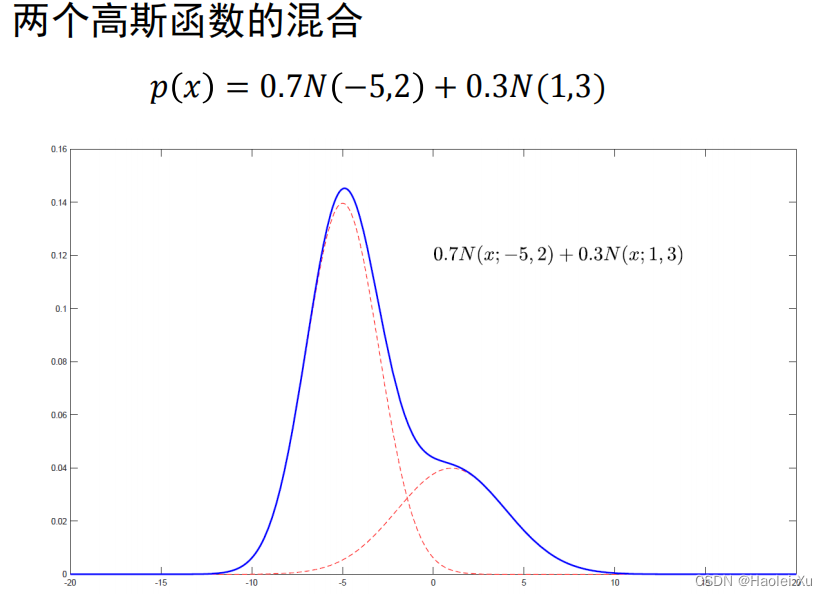
高斯混合模型(GMM)由多个高斯（正态分布）函数的组合构成，即多个高斯函数以不同的权重叠加起来
$p(\mathbf{x})={\sum }_{k=1}^M{a}_{k}N(\mathbf{x};{\mathbf{u}}_k,{\mathbf{\Sigma }}_k)$
例子

推导

GMM 需要估计的参数：
$\theta =({\alpha }_1,\cdots ,{\alpha }_M,{\mathbf{\mu }}_1,\cdots ,{\mathbf{\mu }}_M,{\Sigma }_1,\cdots ,{\Sigma }_M)$
如果取对数求导极值点方程是复杂的超越方程组，很难直接求解
一般使用 EM 算法
如何理解？
GMM就是在估计每个样本究竟来源于哪个高斯分布（标签，或者理解为PPT里的隐变量）并给出参数的估计结果，是一种聚类算法，下面的过程和KMeans聚类非常像，实际上KMeans就是退化后的GMM。
先将$\theta =({\alpha }_1,\cdots ,{\alpha }_M,{\mathbf{\mu }}_1,\cdots ,{\mathbf{\mu }}_M,{\Sigma }_1,\cdots ,{\Sigma }_M)$随机初始化，这个初始化实际上是有讲究的，后面说。

E步

如果是第一次E步，
就拿随机初始化的$\theta =({\alpha }_1,\cdots ,{\alpha }_M,{\mathbf{\mu }}_1,\cdots ,{\mathbf{\mu }}_M,{\Sigma }_1,\cdots ,{\Sigma }_M)$计算标签，开启迭代滚雪球。否则拿M优化调整过的参数。
${\hat{y}}_i=\arg \underset{1\le k\le M}{*max}{\alpha }_{k}N({\mathbf{x}}_i;{\mathbf{\mu }}_k,{\Sigma }_k)$
我的理解是，这玩意儿说白了就是最小错误率贝叶斯估计。
${\alpha }_k$可以理解为类别先验概率
$N({\mathbf{x}}_i;{\mathbf{\mu }}_k,{\Sigma }_k)$可以理解为类条件概率密度

M步

E步计算完了标签，那就把各个正态分布的参数重新计算下，并且根据各不同类别的数量计算概率${\alpha }_i$
${\hat{\alpha }}_k=\frac{1}{n}{\sum }_{i=1}^{n}I(y_i=k)$
${\hat{\mathbf{\mu }}}_k=\frac{{\sum }_{i=1}^{n}I(y_i=k){\mathbf{x}}_i}{{\sum }_{i=1}^{n}I(y_i=k)}$
${\hat{\Sigma }}_k=\frac{{\sum }_{i=1}^{n}I(y_i=k)({\mathbf{x}}_i-{\hat{\mathbf{\mu }}}_k)({\mathbf{x}}_i-{\hat{\mathbf{\mu }}}_k{)}^t}{{\sum }_{i=1}^{n}I(y_i=k)}$
公式里的$I$是指示函数
接着把更新好的参数丢回E步迭代

KMeans与GMM的关系

如果进一步假设，每个聚类的先验概率相同，协方差矩阵均为${\sigma }^2\text{I}$
则$p(\mathbf{x})=\frac{1}{K}{\sum }_{k=1}^{K}N(\mathbf{x};{\mathbf{\mu }}_k,{\sigma }^{2}I)$
这就是大名鼎鼎的KMeans
刚刚提到的初始化问题，我记得sklearn库的GMM源码就是拿KMeans做初始化的。提一句，GMM对初始化的参数非常敏感。

算法

一般形式的EM算法

伪代码

例题

硬币具体情况看PPT


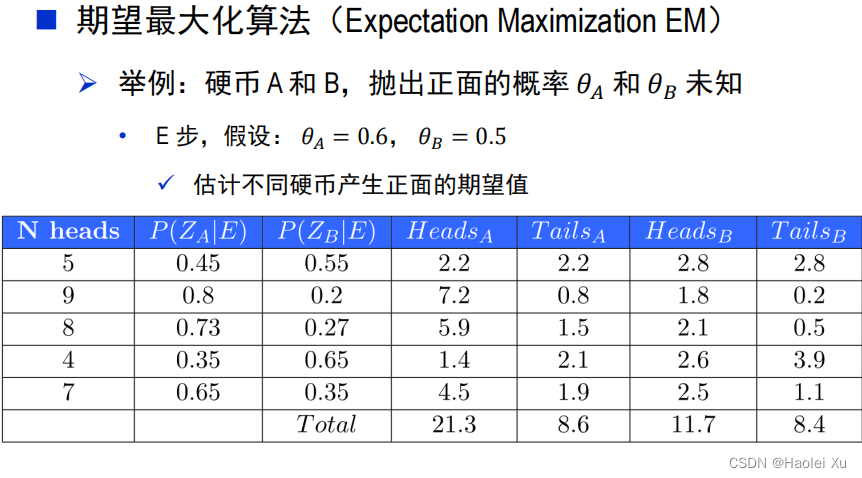
值得注意的是，抛硬币的例题用的是模糊数学，不是非此即彼。比如第一行，B朝上的期望为2.8要比A高，按照之前GMM那里的算法应该是把这个硬币认作B，计算总数的时候5个人头应该全是B类硬币的。这里不是。模糊数学的概念在第14讲也会出现。

第十二讲 隐马尔可夫模型（1）

我们讲到的隐马尔可夫模型都指一阶马尔可夫链

基本假设

假设1：马尔可夫假设（状态构成一阶马尔可夫链）
$P(w_i|w_{i-1}\dots w_1)=P(w_i|w_{i-1})$
假设2：不动性假设（状态转移概率与具体时间无关）
假设3：输出独立性假设（输出仅与当前状态有关）
$P(v_1,\cdots ,v_T|w_1,\cdots ,w_T)=\prod _{t=1}^{T}P(v_t|w_t)$

模型图

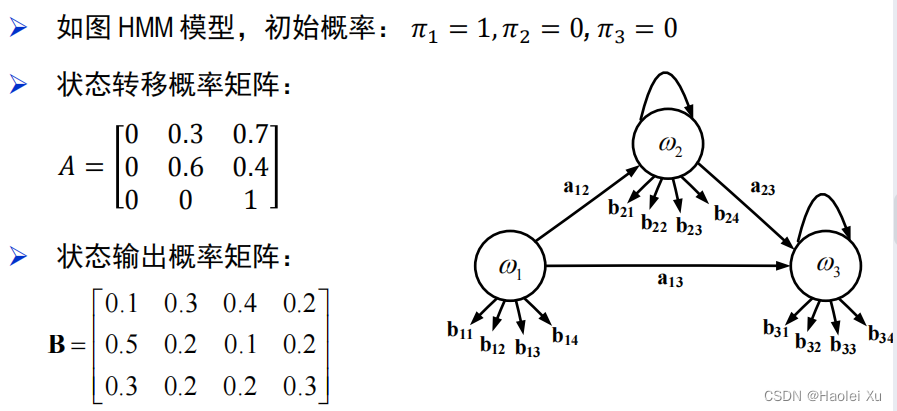
估值问题

呃，考试考了个最简单的估值问题

前向迭代算法

跟朱东杰讲的《算法》一模一样的，披个皮而已

例题

直接看题吧，上复习笔记，别算错就行。

第十三讲 隐马尔可夫模型（2）

解码问题

本质就是动态规划
跟朱东杰讲的那啥街区一模一样的

Viterbi算法

动规表达式
${\delta }_i(t+1)=\underset{1\le j\le M}{\max }[{\delta }_j(t)a_{ji}]b_{iO(t+1)}$

例题

虚线是动态规划过程中被淘汰掉的

学习问题

比较难，且明确不考
愉快跳过

第十四讲 聚类分析

这一部分《机器学习》讲得比较全了，基本都有，只是多讲了些指标啥的。考试考了无监督有监督的区别，送分。
直接看笔记吧，结合PPT看看就行。（博客越写越水了属于是

第十五讲 集成学习

Bagging

典型的比如随机森林，多棵树投票表决，多数通过

Boosting

Bagging 算法属于并行化的集成学习方法，基分类器之间互无关联
而Boosting 算法是序列化的集成学习，下一个基分类器的学习需要根据之前的学习结果来调整，比较有名的是AdaBoost
其思想是对样本进行加权抽样，根据前一个分类器的训练结果，下一个分类器抽到之前错误样本的概率增加，正确样本的概率减小。

Stacking

基本思想：与其使用普通函数（如：hard voting）来集成多个分类器的预测，为什么不训练一个模型来进行集成？

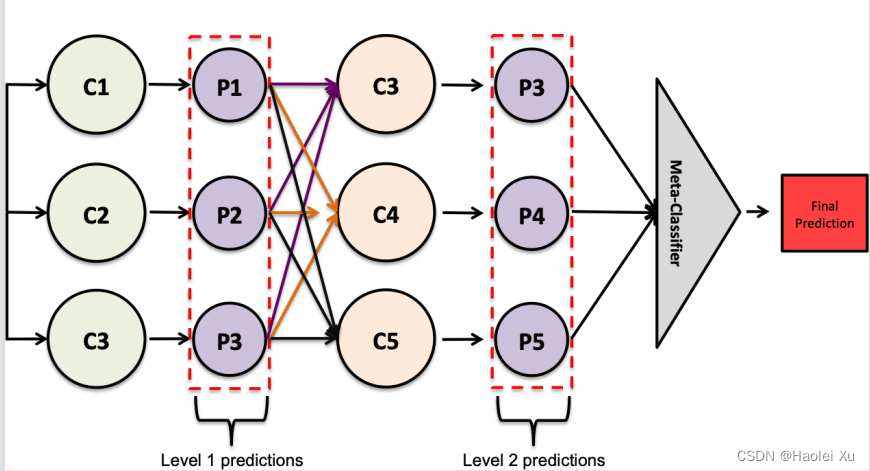
神经网络的集成

直接集成困难，因为训练一个神经网络模型计算量大，时间长
使用Dropout

写在最后

关于考试

考试占总成绩的60%，全是大题，总体来说非常简单，我的卷面是100。一查教务系统发现排第3，说明还有两个卷王连实验带卷子都是满分，果然我是废物。基本都是课上讲过的例题，稍微复习下有点印象都会做，丁老师老好人了。
以下是回忆，不一定准确
1、（1）计算准确率召回率f1（2）计算正确率错误率
2、（1）监督学习和非监督学习的区别（2）用kmeans对样本分类
3、（1）证明后验概率满足逻辑回归的分类面是线性（2）求泊松分布的最大似然估计函数
4、（1）画出HMM模型图（2）HMM估值问题
5、（1）感知器多分类算法中一对一和一对多的分类准则（2）感知器算法计算题（3）SVM计算题
6、（1）PCA降维和LDA降维哪些区别（2）PCA计算题

关于实验

实验占40%，总共4个实验，一个10分，前三个挺简单，好好做基本都能拿满。最后一个实验打榜赛，准确率越高分数就越高，我应该是这里扣了一分，最后这门课总分99hhh。给的Fashion-Mnist数据集，数据集经过了丁老师独家处理，经过了PCA降维（784到76维），每个维度做了随机线性变换，相当于加密处理了吧，因为是公开数据集，不然就都知道答案了。
这个实验个人感觉意义不大，最后大家几乎都是SVM调调参数，网格搜索下，最后测试集听天由命。因为特征是给死的，所以也整不出新活，建议不要做无用功。说下自己的情况，神经网络都试了，没啥用，因为特征是一维，神经网络效果不佳意料之中。当时还想了歪主意，想把这些PCA处理过的还原成784（28*28）维，毕竟2D特征肯定更适合CNN。有些大佬还试过transformer和GAN，都没用，这么少数据量直接劝退。某许姓男子还给我推荐了autolearning的深度学习框架，确实🐂🍺，一键训练了20多个机器学习模型，决策树、随机森林、boosting等等等一大堆，还自带超带参数搜索的，但是这些模型都不如SVM，最好的还是差了SVM一个多百分点。
至于原因吗，无疑是一维的特征没活可整。如果你细究原因的话会发现，一维特征很难区分Fashion-Mnist里相近的一些服装，比如T恤、衬衫，当时我记得是有3种极易混淆的，自己看下面的混淆矩阵热力图体会下。一维特征+机器学习算法几乎束手无策，至少班上没人做出来。去paper with code上看排行榜，最强的想都不用想是2D特征，先做了个锐化，然后效果出奇的好。

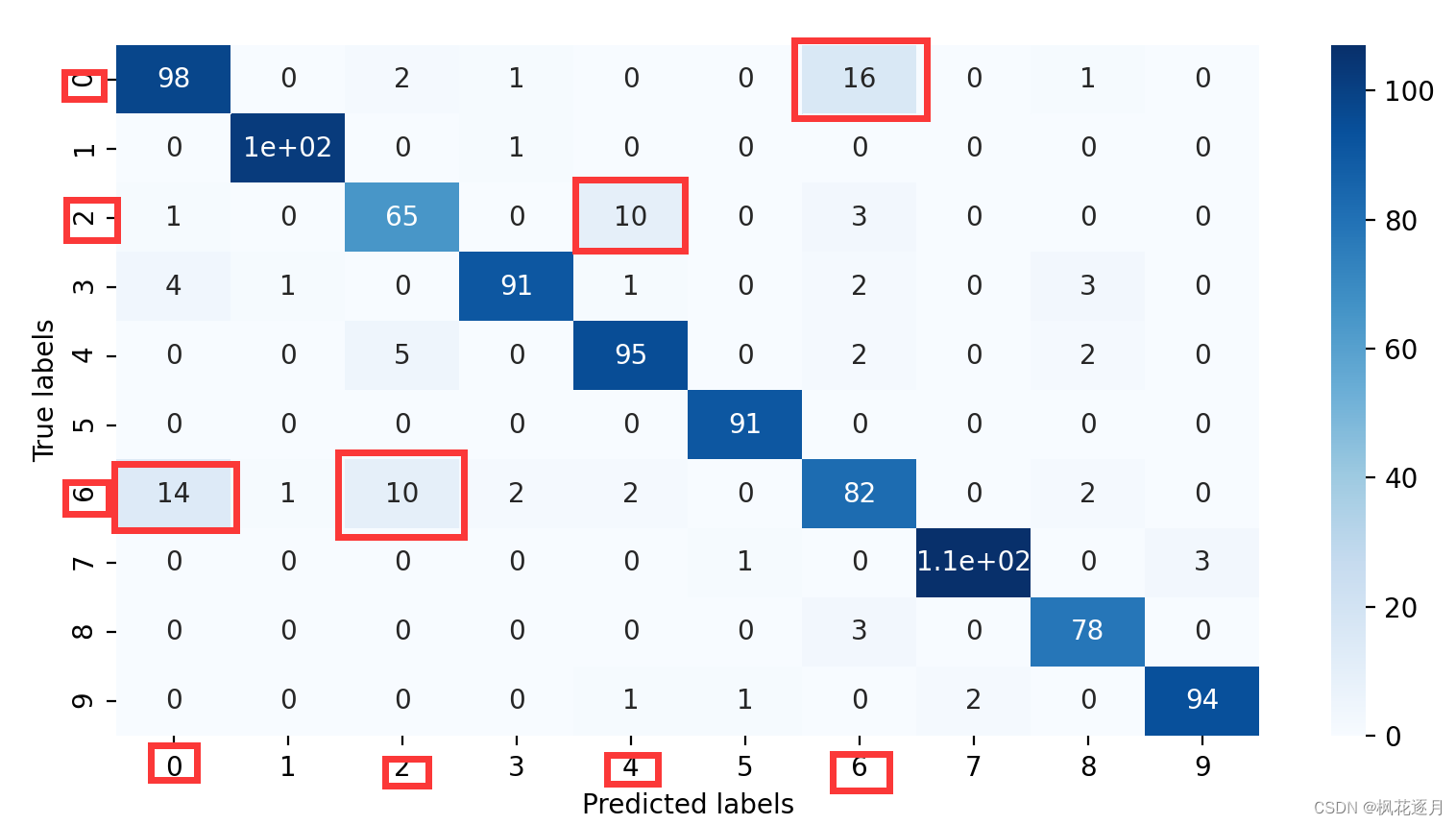
省流：建议直接摆烂，SVM永远滴神。

总结

祝大家都能学有所成，取得好成绩。