了解EM算法

最新推荐文章于 2023-12-20 10:16:34 发布

qq_53303365

最新推荐文章于 2023-12-20 10:16:34 发布

阅读量1.6k

点赞数 2

文章标签：算法

本文链接：https://blog.csdn.net/qq_53303365/article/details/123161721

版权

EM算法是数学建模中很重要的一中方法，在老师的介绍下，我决定自学这个算法。

一、EM算法的思想和作用：

思想：首先，根据已经观测到的数据估计参数值，然后由参数值估计出缺失数据的值，再根据估计出的缺失数据和之前已经观测到的数据对参数值重新估计，反复迭代，直至收敛。

作用：隐变量估计。

二、预备知识：

1.极大似然估计：

似然函数：似然函数和概率函数密不可分，可以说是采用不同角度对一个问题看法。

以下转自一位博主（极大似然估计也在他的文章中有讲解，我认为举的例子很形象）：

对于这个函数：

P ( x ∣ θ )

输入有两个：x表示某一个具体的数据；θ表示模型（如正态分布）的参数。

如果 θ 是已知确定的，x 是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点x，其出现概率是多少。

如果 x 是已知确定的，θ 是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现x这个样本点的概率是多少。
————————————————
版权声明：本文为CSDN博主「nebulaf91」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/u011508640/article/details/72815981

注意：通常在得到似然函数后，会对似然函数进行对数化，再进行求导，从而得到使某样本点出现概率最大的参数 θ 的值。

2.Jensen不等式：

如果f是凸函数（二阶导都不小于0），X是随机变量，那么： $E(f(X))\geqslant f(E(X))$ 。当且仅当X是常量时，该式取等号。其中，E(X)表示X的数学期望。

注：Jensen不等式应用于凹函数时，不等号方向反向。当且仅当x是常量时，该不等式取等号。

下面例子转自一位博主：

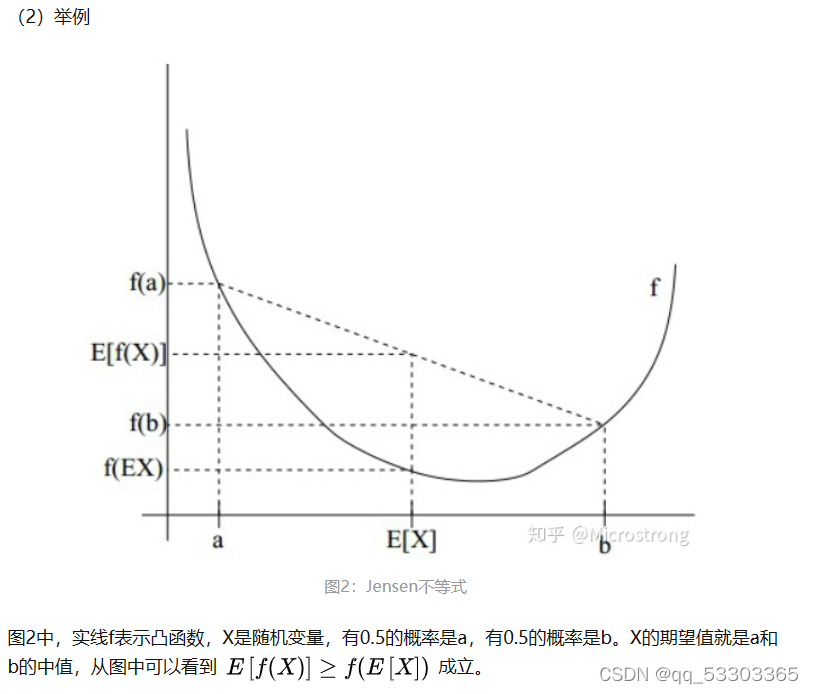
三、EM算法：

EM算法又称期望最大化算法（Expection-Maxium)，该算法需要进行迭代直至参数值收敛，在一次迭代过程中，我们先猜想隐含数据（E步），接着基于观察数据和猜测的隐含数据一起来极大化对数似然，求解我们的模型参数（M步)。

备注：

arg max f(x): 当f(x)取最大值时，x的取值

arg min f(x)：当f(x)取最小值时，x的取值

推导：

对于n个样本观察数据，找出样本的模型参数θ, 极大化模型分布的对数似然函数如下：

$\hat{\theta}=argmax\sum_{i=1}^{n}{logp(x_{i};\theta)}$ （已经对数化）

如果我们得到的观察数据有未观察到的隐含数据，即对于一个 $x_{i}$ ，有 $z_{i}$ （可看成包含多种可能的事件，并且服从某一分布）的情况，此时我们极大化模型分布的对数似然函数如下：

$\hat{\theta}=argmax\sum_{i=1}^{n}{logp(x_{i};\theta)}=argmax\sum_{i=1}^{n}{log\sum_{z_{i}}^{}{p(x_{i},z_{i};\theta)}}$

上面这个式子是根据 $x_{i}$ 的边缘概率计算得来，没有办法直接求出θ。因此需要一些特殊的技巧，使用Jensen不等式对这个式子进行缩放如下：

$\begin{align*} \sum_{i=1}^{n}{log\sum_{z_{i}}^{ }{p(x_{i},z_{i};\theta)}}=\sum_{i=1}^{n}{log\sum_{z_{i}}^{ }{Q_{i}(z_{i})\frac{p(x_{i},z_{i};\theta)}{Q_{i}(z_{i})}}} (1) \\ \geq \sum_{i=1}^{n}{\sum_{z_{i}}^{ }{Q_{i}(z_{i})log\frac{p(x_{i},z_{i};\theta)}{Q_{i}(z_{i})}}}(2) \end{align*}$

(1)式是引入了一个未知的新的分布，分子分母同时乘以它得到的。
(2)式是由(1)式根据Jensen不等式得到的。由于 $\sum Q_{i}(z_{i})\frac{p(x_{i},z_{i}; \theta )}{Q_{i}(z_{i})}$ 为 $\frac{p(x_{i},z_{i};\theta)}{Q_{i}(z_{i})}$ 的期望，且log(x)为凹函数，根据Jensen不等式可由(1)式得到(2)式。
上述过程可以看作是对 $logl(\theta)$ 求了下界（ $l(\theta)=\sum_{i=1}^{n}{logp(x_{i};\theta)}$ ）。对于 $Q_{i}(z_{i})$ 我们如何选择呢？假设θ已经给定，那么 $logl(\theta)$ 的值取决于 $Q_{i}(z_{i})$ 和 $p(x_{i},z_{i})$ 。我们可以通过调整这两个概率使(2)式下界不断上升，来逼近的真实值。那么如何算是调整好呢？当不等式变成等式时，说明我们调整后的概率能够等价于了。按照这个思路，我们要找到等式成立的条件。

如果要满足Jensen不等式的等号，则有： $\frac{p(x_{i},z_{i};\theta)}{Q_{i}(z_{i})}=c$

（c为常数）

由于 $Q_{i}(z_{i})$ 是一个分布，所以满足: $\sum_{z}^{ }{Q_{i}(z_{i})}=1$ ，则 $\sum_{z}^{ }{p(x_{i},z_{i};\theta)}=c$ 。

由上面两个式子，我们可以得到：

$Q_{i}(z_{i})=\frac{p(x_{i},z_{i};\theta)}{\sum_{z}^{ }{p(x_{i},z_{i};\theta)}}=\frac{p(x_{i},z_{i};\theta)}{p(x_{i};\theta)}=p(z_{i}|x_{i};\theta)$ （表示在xi条件下zi发生的概率）

至此，我们推出了在固定其他参数θ后， $Q_{i}(z_{i})$ 的计算公式就是后验概率，解决了如何选择 $Q_{i}(z_{i})$ 的问题。

如果 $Q_{i}(z_{i})=p(z_{i}|x_{i};\theta)$ ，则(2)式是我们包含隐藏数据的对数似然函数的一个下界。如果我们能最大化(2)式这个下界，则也是在极大化我们的对数似然函数。即我们需要最大化下式：

$argmax\sum_{i=1}^{n}{\sum_{z_{i}}^{ }{Q_{i}(z_{i})log\frac{p(x_{i},z_{i};\theta)}{Q_{i}(z_{i})}}}$

上式也就是我们的EM算法的M步，那E步呢？解决了如何选择 $Q_{i}(z_{i})$ 的问题，这一步就是E步，该步建立了 $l\left(\theta \right )$ 的下界。

注意：在记忆公式时不要死记硬背数学公式，而是要理解每个式子代表的实际意义，这样记得更牢。

算法流程：

————————————————
版权声明：本文为CSDN博主「Microstrong0305」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/program_developer/article/details/81878355

被引用博主举的抛硬币例子十分形象生动，但是在这个例子中需要注意的是：

在每一次的迭代中，由于这个例子可以直观地看出每次迭代对应的参数值（使已经发生的现实情况最有可能发生的参数值），所以没有进行求导等求极大值点的操作；

四、总结：

EM算法在数学建模，尤其是根据已有数据求未知参数（定值）中有很重要的作用，是数学建模中一个重要的方法。

qq_53303365

关注

2
点赞
踩
8

收藏

觉得还不错? 一键收藏
0
评论
了解EM算法

EM算法是数学建模中很重要的一中方法，在老师的介绍下，我决定自学这个算法。一、EM算法的思想和作用：思想：首先，根据已经观测到的数据估计参数值，然后由参数值估计出缺失数据的值，再根据估计出的缺失数据和之前已经观测到的数据对参数值重新估计，反复迭代，直至收敛。作用：隐变量估计。二、预备知识：1.极大似然估计：...
复制链接

扫一扫