MK趋势性分析、MK突变性分析（线性回归法、M-K法、Spearman法）~“附代码实例”

一、趋势性分析方法

1.线性回归法

        注意：结果判断查的是自由度为（n-2）的T分布表。

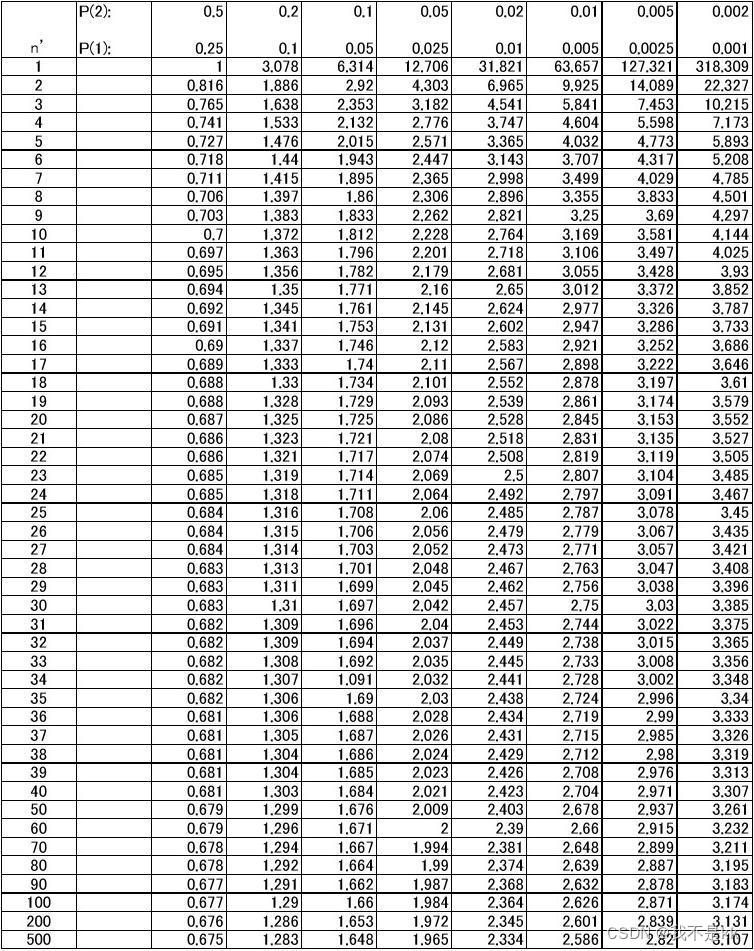
 2.Mann-Kendall检验法

 

        注意：结果判断查的是标准正态分布表。Z的绝对值在大于1.64、1.96、2.58时
别表示通过了置信度90%、95%和99%的显著性检验。

3. Spearman秩检验法

 注意：结果判断查的是自由度为（n-2）的T分布表。

二、突变性分析方法

1.Mann-Kendall突变检验法

 2.累积距平法

        注意：突变性分析（突变年份）常多种方法互相对比印证。

三、 实例分析

1.问题

现有KK站1956年~2016年年径流量数据，请分析其趋势性与突变性。

2.趋势性分析

2.1 线性回归法

       由最小二乘法得线性趋势线为（x为流量Q，t为年份）：

        取显著性水平α=0.05，统计量T满足|T|<t（0.025,58）=2.01，可见序列的变化趋势不显著，即不显著的减小趋势。

2.2 Mann-Kendall检验法

       （1）MATLAB代码如下：

% M-K趋势分析
clear all;
clc;
load Time_Q_data;         %KK站时间流量序列（时间、年、枯期、汛期）
%y=KK1956_2016;
y=DATA(:,4);              %数据列，可调整为各期计算
n=length(y);        % y是待检测数据序列
s=0;
for k=1:n-1
    for j=k+1:n
        s=s+sign(y(j)-y(k));
    end
end
v=(n*(n-1)*(2*n+5))/18;
if s==0
    z=0;
elseif s>0
    z=(s-1)/sqrt(v);
else
    z=(s+1)/sqrt(v);
end
z
% z>0为上升趋势，z<0为下降趋势。
% KK显著性水平临界值为1.96（0.05），临界值不随系列长度而变（服从均值为0的正态分布）。

       （2）计算结果

       取显著性水平α=0.05，Mann-Kendall检验法计算年统计量Z分别为-0.62，年统计量|Z|<z0.025=1.96，因此Mann-Kendall检验法计算结果为KK水文站年平均流量序列呈不显著减小趋势。

2.3 Spearman秩检验法

       （1）计算结果

       取显著性水平α=0.05，Spearman秩检验法计算年统计量T为0.50，年统计量|T|<t0.025,58=2.01，因此Spearman秩检验法计算结果为KK水文站年平均流量序列呈不显著的减小趋势。

3.突变性分析

       （1）MATLAB代码如下：

% M-K突变分析
clear all;
clc;
load KK_Q;         %KK站时间流量序列（时间、年）
x=DATA(:,1);              %时间列,DATA同KK
y=DATA(:,4);              %数据列，可调整为各期计算
n=length(y);
SK=zeros(size(y));
UFK=zeros(size(y));
s=0;
for i=2:n
    for j=1:i
        if y(i)>y(j)
            s=s+1;
        else
            s=s+0;
        end
    end
    SK(i)=s;
    E=(i*(i-1))/4;
    Var=(i*(i-1)*(2*i+5))/72;
    UFK(i)=(SK(i)-E)/sqrt(Var);
end
y2=zeros(size(y));
SK2=zeros(size(y));
UBK=zeros(size(y));
s=0;
for i=1:n
    y2(i)=y(n-i+1);
end
for i=2:n
   for j=1:i
         if y2(i)>y2(j)
           s=s+1;
         else
           s=s+0;
         end
   end
   Sk2(i)=s;
   E=i*(i-1)/4; 
  Var=i*(i-1)*(2*i+5)/72;
  UBk(i)=0-(Sk2(i)-E)/sqrt(Var);
end
UBk2=zeros(size(y));
for i=1:n
   UBk2(i)=UBk(n-i+1);
end
% 绘图用的是UFK和UBK2
% 绘图临界值0.05水平下为±1.96（因为服从均值为0的正态分布）

       （2）计算结果：M-K突变检验、累积距平曲线图如下

        综合判断1968年、1998年为年径流量突变年份。