Leecode 动态规划及背包问题

本文将整理以下leecode原题：

53. 最大子数组和 - 力扣（LeetCode）

152. 乘积最大子数组 - 力扣（LeetCode）

300. 最长递增子序列 - 力扣（LeetCode）

416. 分割等和子集 - 力扣（LeetCode）

---

动态规划

动态规划的题难度一般都很高，而且属于会了一道，拿到下一道一样不会的类型。而且会在看到答案后恍然大悟，很难找到学习的规律。

普遍的动态规划的题型，我们分为几个步骤：

1.确定边界条件：如何初始化

2.确定转移矩阵：即dp[i+1]和dp[i]的关系，这是动态规划问题里最难想到的一步。

思想上：我们需要把整个问题拆解成若干个小问题，一步一步的获得最终的答案。

代码上：一般需要通过if等条件判断，并且包含了max等比较操作。

数学上：想到严格的转移公式是很难的，看到了答案可能想得到，做的时候只能尝试去分解问题，找dp[i+1]和dp[i]的关系。

---

53. 最大子数组和 

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]

输出：6

解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]

输出：1

示例 3：

输入：nums = [5,4,-1,7,8]

输出：23

提示：

1 <= nums.length <= 105

-104 <= nums[i] <= 104

解答思路

这个题一上来很容易会想用前缀和去解决，但是这样搜索还是很耗时，我们用dp的思路去解决。

直接解决这个问题很难，我们想一个问题，子数组中的数字，一定是包含在原nums中的，那我们能不能在原数组中，去建立一个dp矩阵，这个矩阵的任务是去判断每一个i，包含当前i的最大子数组的和是多少，最终的答案从dp中的max获取不就解决了。

那么我们的任务就变成了，求解一个新的dp。

我们来想这个dp的转移关系：dp[i]相比于dp[i-1]而言引入了nums[i]。那么包含nums[i]的最大子数组可能有什么情况呢，一个是dp[i-1]<0，这个时候，显然dp[i]=nums[i]；如果dp[i-1]>0，注意到dp[i-1]是一定包含了nums[i-1]的，那么此时的dp[i]=nums[i]+dp[i-1]。

这样梳理下来，我们的代码逻辑就清晰了：

class Solution(object):
    def maxSubArray(self, nums):
        for i in range(1,len(nums)):
            nums[i] = nums[i]+max(nums[i-1], 0)
        return max(nums)

看到最后的实现代码会发现，问题解决得很简单。

---

152.乘积最大子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位 整数。

示例 1:

输入: nums = [2,3,-2,4]

输出: 6

解释: 子数组 [2,3] 有最大乘积 6。

示例 2:

输入: nums = [-2,0,-1]

输出: 0

解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

提示:

1 <= nums.length <= 2 * 104

-10 <= nums[i] <= 10

nums 的任何前缀或后缀的乘积都 保证 是一个 32-位整数

解答思路

这个题看上去和上一个题很像，一个是求最大子数组的和，一个是求最大子数组的积。但是这里会遇到一个更难处理的问题，就是dp[i]的最优结果并不是直接由dp[i-1]所决定的，这是因为nums中可能包含了负数，如果nums[i]为负数，那么就有可能把nums[i-1]时出现的最小的子数组变成最大。

想到了这一层，那么就不难想到怎么解决这个问题了。

我们在dp的时候，同时记录两个数组，一个保存最大的结果，一个保存最小的结果（大概率是个负数）。每一次更新时，就需要从nums[i]*max, nums[i]*min, nums[i]中去比较，得到最大最小值。

这里注意为什么加上num[i]，这是把dp[i-1]=0的情况考虑进去了，如果nums[i]>0时，就需要新起一段。

最后在比较的过程当中，记录下最大的max中的数，返回结果即可。

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        ans, num_max, num_min = nums[0], nums[0], nums[0]
        for i in range(1, len(nums)):
            maxn, minn = num_max, num_min
            num_max = max(nums[i], nums[i]*maxn, nums[i]*minn)
            num_min = min(nums[i], nums[i]*maxn, nums[i]*minn)
            ans = max(ans, num_max)
        return ans

---

300.最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]

输出：4

解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]

输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]

输出：1

提示：

1 <= nums.length <= 2500

-104 <= nums[i] <= 104

解答思路

最长的递增子序列，要注意子序列的定义，不需要连续。

最重要的还是思考怎么设计转移的关系。

直接想太抽象了，仿佛无法直接找到dp[i]和dp[i-1]的关系，我们不知道nums[i-1]的最长递增子序列的最后一个元素是多少，但是如果我们能够用nums[i]跟这个最长递增子序列的最后一个元素比较大小，那么就可以得到dp[i]的值了，因此，我们在考虑转移关系时，不光需要考虑dp[i-1]，还需要考虑dp[0:i]的值，找到最长的递增子序列，并且判断是否需要+1。

因此，代码如下：

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        
        n = len(nums)
        dp = []
 
        for i in range(n):
            # dp的初始化，有一个元素，结果就至少为1
            dp.append(1)

            # 在0~i-1之间进行转移 
            for j in range(i):
                if nums[i]>nums[j]:
                    dp[i] = max(dp[i], dp[j]+1)
        return max(dp)
                

这道题的核心就在于，转移矩阵有的时候，也需要考察dp[i]之前的所有元素。

---

416.分割等和子集

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]

输出：true

解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]

输出：false

解释：数组不能分割成两个元素和相等的子集。

提示：

1 <= nums.length <= 200

1 <= nums[i] <= 100

解答思路

这个题是不能用简单的dp去解决的。其实不难发现，我们的目标可以等价于问nums中有没有一些数的和能够等于sum(nums)/2。

这个等价的问题，我们就可以用背包问题解决。

背包问题

代码随想录 (programmercarl.com)

代码随想录里对于这个问题讲的很清楚。就不班门弄斧，这里主要浓缩一下，最核心的思路。（建议先看讲解，再往下读）。

我们先直接搬一个背包问题的模板代码：

def test_2_wei_bag_problem1():
    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagweight = 4

    # 二维数组
    dp = [[0] * (bagweight + 1) for _ in range(len(weight))]

    # 初始化
    for j in range(weight[0], bagweight + 1):
        dp[0][j] = value[0]

    # weight数组的大小就是物品个数
    for i in range(1, len(weight)):  # 遍历物品
        for j in range(bagweight + 1):  # 遍历背包容量
            if j < weight[i]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

    print(dp[len(weight) - 1][bagweight])

test_2_wei_bag_problem1()

根据上面代码来理解会好很多：

1.转化为原始的背包问题：

原始背包问题有三个重要的初始值：物体的重量、物体的价值、背包的容量。关键就在于找到这三个量是多少。

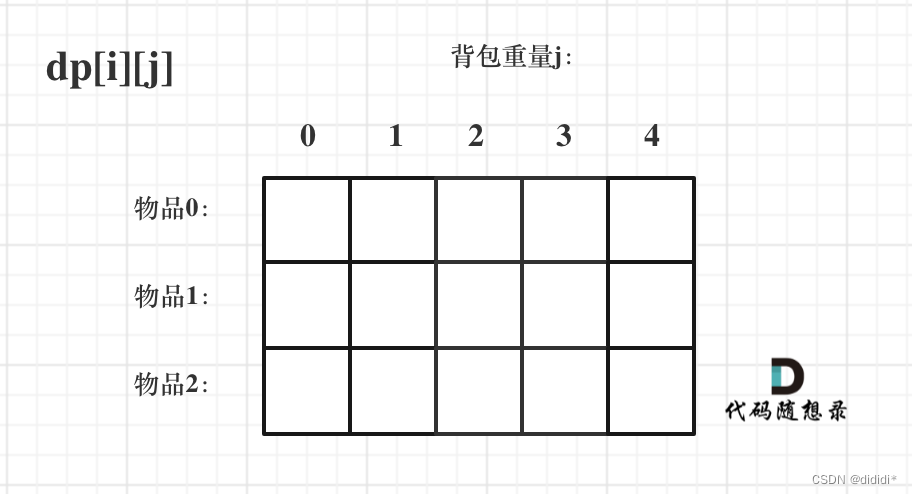
2.dp[i][j]矩阵

这个矩阵更是背包问题中的核心！！！

这里建议按照下面这个图，把矩阵就建立出来想问题，会直观很多。

在最原始的背包问题中，这个dp[i][j]的含义表示为：

表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

在不同的题里，dp[i][j]的含义可能是不一样的，这需要灵活的变通。

3.初始化

关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

一般来说，初始化的时候，考虑上面的第一行和第一列就行。

4.如何转移

这涉及到具体的问题，对于原始背包问题，需要价值最大，因此，就需要考虑最大的价值是多少，就变成了背包问题最经典的转移代码：

for i in range(1, len(weight)):  # 遍历物品
        for j in range(bagweight + 1):  # 遍历背包容量
            if j < weight[i]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

简单解释一下：

在先遍历物品的情况下，dp[i][j]是由dp[i-1][j]转移而来的。

• 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
• 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

那么，回到这个题上，我们就可以用背包问题来解决，这个问题变成：

nums里，选若干个数字，每个数字的大小就是这个物体的体积，能不能刚好装满容量为sum(nums)/2的背包，能够装满就返回True，不能就返回False。

按照这个思路，代码如下（有详细的注释）：

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        n =len(nums)
        total = sum(nums)
        maxNum = max(nums)

        if n < 2:
            return False
        if total%2 == 1:
            return False

        target = int(total/2)
        if maxNum > target:
            return False

        # 建立背包，dp[i][j]表示在nums[0:i]这些数字里面拿，能否取出和为j的子数组
        dp = [[False]*(target+1) for _ in range(n)]

        # 初始化dp
        # 第一列，j=0的时候都是True，不需要加入num
        for i in range(0, n):
            dp[i][0] = True
        # 第一行，只能取nums[0],因此，只有nums[0][nums[0]]可以为true
        dp[0][nums[0]] = True

        # 转移
        for i in range(1,n):
            for j in range(1,target+1):
                # dp[i][j]其实是从dp[i-1][j]转移来的

                # j的值比nums[i]小的时候，只要拿了nuns[i]，就一定false了
                # 因此这种情况下不拿nums[i]，这部分的dp[i][j]=dp[i-1][j]
                if j<=nums[i]:
                    dp[i][j]=dp[i-1][j]
                else:
                # 当j比nums[i]大的时候，可以根据是否要计入nums[i]分成两个部分，两部分相或
                # 1.不加入nums[i]，那么dp[i][j]=dp[i-1][j]
                # 2.加入nums[i]，那么dp[i][j]=dp[i-1][j-nums[i]]
                    dp[i][j]= dp[i-1][j] | dp[i-1][j-nums[i]]
        return dp[n-1][target]