如何使用MatLab对CSI的相位进行矫正

目录

一、前言

二、操作步骤

1、处理的大致过程

2、解卷绕

3、线性变换

4、MATLAB代码实现

三、实验结果

---

一、前言

目前大部分基于CSI的无线被动定位方案都只使用CSI的幅值响应信息，忽略了CSI的相位响应信息，因为其原始相位响应信息中含有很大的随机噪声和相位误差。然而，有文献表明，经过校准后的CSI相位对目标位置的变化更为敏感，所以对CSI相位的处理便尤为重要。由于采集到的CSI样本信号，在传输的过程中会受到周围环境的噪声干扰，同时由于硬件限制等原因会产生相位偏移，可以采用一种简单而有效的线性拟合的方法进行相位，消除由于残余的载波频率误差及时钟同步误差造成的相位偏移，以此来获得CSI的真实相位。

二、操作步骤

1、处理的大致过程

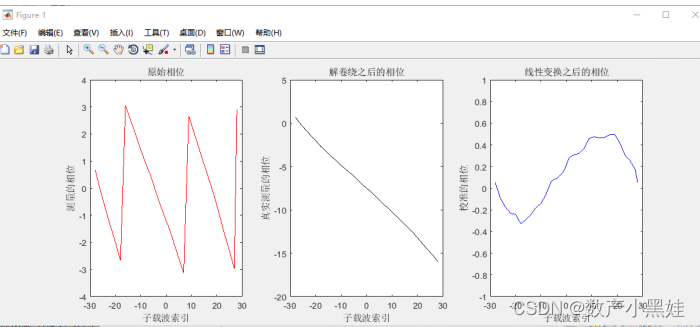
原始相位→解卷绕→线性变换→校正后的相位（真实相位）

注：由于CSI的相位存在循环性，提取出的CSI相位是折叠的，因此需要先对CSI相位进行解卷绕，得到解卷绕后的相位后，再对其进行线性变换处理。

2、解卷绕

MATLAB使用unwrap函数进行解卷绕，使相位在pi处不发生跳变，从而反应出真实的相位变化。实际在默认的情况下，unwrap在检查到数据前后两点的差距在超过π的时候，就认为有跳变，当然其阈值也能通过函数设置。

unwrap函数的完整格式：unwrap(pha,tol,dim)；

pha可为数列或矩阵，tol为判断的阈值，dim参数可以设置对矩阵的行（1表示列，2表示行）。 

a =[2.1415  -3.1415  2.5025  1.7062  1.0361  0.2504  -0.5363  -2.5515  2.9917  2.0832 1.3398];
a_=a';
b=unwrap(a_,pi,1);
hold on
plot(a_,'b-');
plot(b,'r-');
hold off 
c=[a_,b];
disp(c);

当2.1415与-3.1415之间超过阈值π后视为发生跳变，将-3.1415加上或减去2*pi，这里加上2π，得到3.1417，再用2.5025与3.1417相比，两者相差小于π，故不进行解卷绕，以此类推。 

3、线性变换

（1）线性变换算法公式和大致步骤如下所示：

（2）下图为不同带宽的子载波索引序列，可按照自己的实际需求来选取，我这里选择的是20MHz的带宽对应的子载波索引序号。

4、MATLAB代码实现

%参数说明：H_表示原始相位，F表示解绕缠后的矩阵、H表示矫正后的相位
H_=xlsread('test1.xlsx',1,'A1:AD1');
F=unwrap(H_,pi,2); %F表示解卷绕后的矩阵，判断的阙值为pi,2表示对矩阵每一行进行相位矫正
m=[-28,-26,-24,-22,-20,-18,-16,-14,-12,-10,-8,-6,-4,-2,-1,1,3,5,7,9,11,13,15,17,19,21,23,25,27,28];
H_length=length(H_);
%预先分配好内存空间
H=zeros(1,H_length);
%线性变换   
sum=0;
  for t=1:30
     sum=sum+F(t);
  end
  b=(1/30)*sum;
  k=(F(30)-F(1))/(m(30)-m(1));
  for i=1:30  %子载波迭代
  H(i)=F(i)-k*m(i)-b; %H表示校正以后的相位，H_表示实际测量的相位，k表示斜率，b表示截距
    %res=squeeze(H);
  end
hold on
subplot(1,3,1); plot(m,H_,'r-');set(gca,'Xlim',[-30,30]);%原始相位图
title('原始的相位');xlabel('子载波索引');ylabel('相位');
subplot(1,3,2); plot(m,F,'k-');  %解卷绕后的相位图
set(gca,'Xlim',[-30,30]);set(gca,'Ylim',[-25,5]);
title('解卷绕之后的相位');xlabel('子载波索引');ylabel('真实测量的相位');
subplot(1,3,3); plot(m,H,'b-');  %真实相位图
set(gca,'Xlim',[-30,30]);set(gca,'Ylim',[-1,1]);
title('线性变换之后的相位');xlabel('子载波索引');ylabel('校准的相位');
hold off
% disp(H_);
% disp(F);
% disp(H);

三、实验结果

（1）可以看出处理前的相位毫无规律可言，处理后的相位集中分布，说明了线性变换的有效性。

 （2）1500个数据包的1500*30个子载波的相位矫正结果如下图所示：

如有对室内定位之CSI指纹定位感兴趣的，可参考博主往期文章：室内定位之CSI指纹定位_数产小黑娃的博客-CSDN博客

创作不易，感谢支持，您的支持是我进步最大的动力！！！

目前已发现文章抄袭，甚至连变量都不改的，希望支持原创，抄袭文章链接：使用MATLAB进行CSI数据处理_一定要早睡早起呀的博客-CSDN博客