🐺本博主博客:ζั͡ ั͡雾 ั͡狼 ั͡✾的博客
🎀专栏:机器学习
🎀专栏:爬虫
🎀专栏:OpenCV图像识别处理
🎀专栏:Unity2D
⭐本节课理论视频:
⭐本节课推荐其他人笔记:吴恩达机器学习系列课程笔记——第四章
🐺机器学习通过文字描述是难以教学学会的,每一节课我会推荐这个理论的网课,一定要看上面的理论视频!一定要看上面的理论视频!一定要看上面的理论视频!所以我只是通过代码实现,并通过注释形式来详细讲述每一步的原因,最后通过画图对比的新式来看结果比较。
⭐机器学习推荐博主:GoAI的博客_CSDN博客-深度学习,机器学习,大数据笔记领域博主
😊如果你什么都不懂机器学习,那我推荐GoAI的入门文章:机器学习知识点全面总结_GoAI的博客-CSDN博客_机器学习笔记
(1)对上节课一元一次回归进行扩展成矩阵形式
import numpy as np
import matplotlib.pyplot as plt
# 全局变量
# 生成数据
#X中每一行代表一条数据i,代表着一个等式,其中列数代表着变量数,每个变量的系数是不知道的
#每一行数据是y=k0x0+k1x1+k2x2+k3x3+k4x4,
#k是我们要回归的系数向量,x1,x2,x3,x4是每一行数据其中
# k0代表常数,x0恒为1
X =np.array([[5,100,58,-3],
[7,120,59,-3],
[3,140,50,-5],
[10,80,45,-1],
[6,96,55,-7],
[15,200,52,-11],
[11,125,65,-5],
[12,63,100,-3],
[20,500,66,-10]])
#假设K系数为这个,咱们的算法就是逼近这个结果,当然,如果有自己的数据就更好了
preK=[12,-1,2,8]+np.random.random((1,4))
#Y中的数据量等于X矩阵的行数
Y=(np.dot(preK,X.T)+np.random.random()*15).ravel()#加的一项是随机常数项,最后将矩阵转换成数组向量
#开始
# 学习率,在代价函数斜率线上移动的距离步子大小
A = 0.000001
# 迭代次数
time = 100000
#X矩阵中第一列加入x0=1参数
X=np.insert(X,0,np.ones((1,len(X))),axis=1)
#数据个数
m=len(X)
#参数个数
n=len(X[0])
#输出
print(f"有{n}个参数,就是X列数算上常数项所乘的单位1")
print(f"有{m}条数据,就是加常数后X行数")
#系数变量K矩阵就是多元参数的系数,就是我们要递归的重点变量,先给这个矩阵的每个值都赋予初始值1
K=np.ones(n)
# 假设函数,假设是个多元线性函数,每个参数的系数和常数不知道,是要回归算的变量
#返回系数矩阵乘参数矩阵
#下面的变量Xi代表一条数据,既X矩阵的一行
def H(Xi):
global K
return np.dot(K,Xi.T)#xi需要转置,才能得到内积和
# 代价函数L=求和((H(x)-y(x))^2),其中H是关于K矩阵中所有系数参数的函数
# 代价函数就是你估算的值与实际值的差的大小,使得代价函数最小,这样就能不断逼近结果
# 使得代价函数最小,就要使得初始点在斜率线上不断往低处移动,呈现出系数的不断微小移动
# 固定公式格式,推导原理看吴恩达P11
def dL_K(): # 代价函数对矩阵中系数参数k求导
global X,Y,K,m,n
dL_Karr=np.empty(n)#数组用来存放L对每个k求导后的结果
for j in range(n):
ans = 0
for i in range(m):
ans += ((H(X[i]) - Y[i]) * X[i][j]) # 由于k的系数是x,所以求导后还要乘x
dL_Karr[j]=ans
return dL_Karr
def itreation(time): # 迭代,使O1,O2的代价函数趋于最低点
global K
for i in range(time):
#一次迭代过程中代价函数对系数k的导数数组
dL_Karr=dL_K()
# 同时变化,减法原因是正斜率使得O更小,负斜率使得O更大,不断往低处移动即代价函数最小
K=K-A*dL_Karr
if (i % 10000== 0): # 每100次输出一次
print(f"迭代了{i}次,变量的系数矩阵K为{K}")
if __name__ == "__main__":
print(X)
print(Y)
itreation(time)
print(preK)
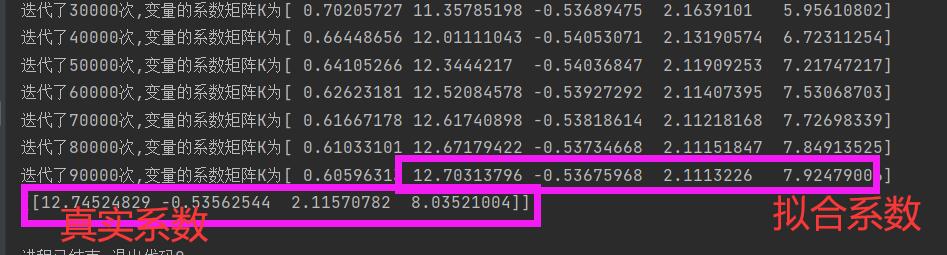
A学习率要调的足够小,K系数矩阵结果才不会发散,但太小迭代的很慢,还有可能超出数组的大小限制,并且结果并不容易找到,所以要做一下吴恩达老师说的归一化步骤是很重要的
(2)加上归一化步骤
import numpy as np
import matplotlib.pyplot as plt
# 全局变量
# 生成数据
#X中每一行代表一条数据i,代表着一个等式,其中列数代表着变量数,每个变量的系数是不知道的
#每一行数据是y=k0x0+k1x1+k2x2+k3x3+k4x4,
#k是我们要回归的系数向量,x1,x2,x3,x4是每一行数据其中
# k0代表常数,x0恒为1
X =np.array([[5,100,58,-3],
[7,120,59,-3],
[3,140,50,-5],
[10,80,45,-1],
[6,96,55,-7],
[15,200,52,-11],
[11,125,65,-5],
[12,63,100,-3],
[20,500,66,-10]])
#假设K系数为这个,咱们的算法就是逼近这个结果,当然,如果有自己的数据就更好了
preK=[12,-1,2,8]+np.random.random((1,4))
#Y中的数据量等于X矩阵的行数
Y=(np.dot(preK,X.T)+np.random.random()*15).ravel()#加的一项是随机常数项,最后将矩阵转换成数组向量
#进行归一化操作
#获取每列平均值
u=np.average(X,axis=0)
#获取没列的标准差
s=np.std(X,axis=0)
#按行复制,构成X同形状矩阵
U=np.repeat([u],len(X),axis=0)
S=np.repeat([s],len(X),axis=0)
#归一化,注意归一化所求的系数矩阵K是(X-U)/S的系数,真正系数,需要将x参数前面的系数合并
X=(X-U)/S
#开始
# 学习率,在代价函数斜率线上移动的距离步子大小
A = 0.0001
# 迭代次数
time = 100000
#X矩阵中第一列加入x0=1参数
X=np.insert(X,0,np.ones((1,len(X))),axis=1)
#数据个数
m=len(X)
#参数个数
n=len(X[0])
#输出
print(f"有{n}个参数,就是X列数算上常数项所乘的单位1")
print(f"有{m}条数据,就是加常数后X行数")
#系数变量K矩阵就是多元参数的系数,就是我们要递归的重点变量,先给这个矩阵的每个值都赋予初始值1
K=np.ones(n)
# 假设函数,假设是个多元线性函数,每个参数的系数和常数不知道,是要回归算的变量
#返回系数矩阵乘参数矩阵
#下面的变量Xi代表一条数据,既X矩阵的一行
def H(Xi):
global K
return np.dot(K,Xi.T)#xi需要转置,才能得到内积和
# 代价函数L=求和((H(x)-y(x))^2),其中H是关于K矩阵中所有系数参数的函数
# 代价函数就是你估算的值与实际值的差的大小,使得代价函数最小,这样就能不断逼近结果
# 使得代价函数最小,就要使得初始点在斜率线上不断往低处移动,呈现出系数的不断微小移动
#注意归一化所求的系数矩阵K是(X-U)/S的系数,真正系数,需要将x参数前面的系数合并
# 固定公式格式,推导原理看吴恩达P11
def dL_K(): # 代价函数对矩阵中系数参数k求导
global X,Y,K,m,n
dL_Karr=np.empty(n)#数组用来存放L对每个k求导后的结果
for j in range(n):
ans = 0
for i in range(m):
ans += ((H(X[i]) - Y[i]) * X[i][j]) # 由于k的系数是x,所以求导后还要乘x
dL_Karr[j]=ans
return dL_Karr
def itreation(time): # 迭代,使O1,O2的代价函数趋于最低点
global K
for i in range(time+1):
#一次迭代过程中代价函数对系数k的导数数组
dL_Karr=dL_K()
# 同时变化,减法原因是正斜率使得O更小,负斜率使得O更大,不断往低处移动即代价函数最小
K=K-A*dL_Karr
if (i % 10000== 0): # 每100次输出一次
print(f"迭代了{i}次,变量的系数矩阵K为{K}")
if __name__ == "__main__":
print('归一化X',X)
print(Y)
itreation(time)
print('归一化系数(第一个是常数)',K,)
#注意归一化所求的系数矩阵K是(X-U)/S的系数,真正系数,需要将x参数前面的系数合并
#忽略前一位常数,计算真正系数
K[1:]=K[1:]/s
#利用真正系数,计算真正常数
K[0]=K[0]-np.sum(K[1:]*u)
print('真正系数矩阵',K)
print('目标系数',preK)
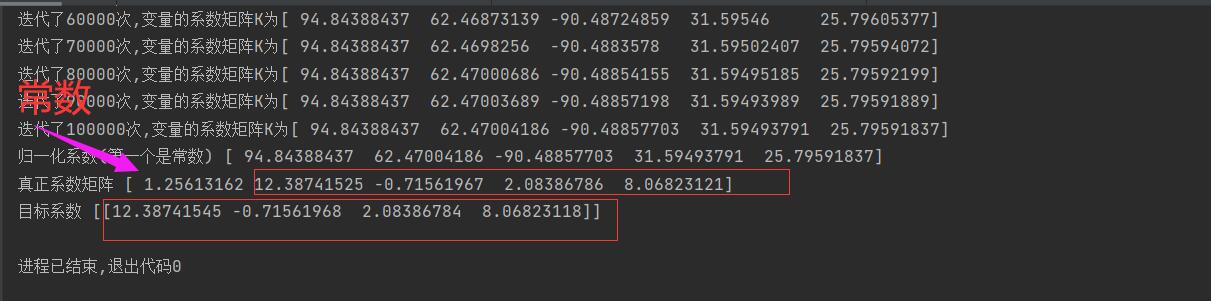
可见,归一化后,A可以大一些,10000次K已经变化微小了,递归更快,更准



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










