有限域计算-GF(2^N) 乘法

1.首先要知道有限域问题通常可以转化为 多项式计算，涉及到 不可约多项式

例如 2^8  要将8位（这里指的是八个而二进制位 0000 0000）全部利用到 我们计算乘法的时候 很容易就会计算到 x^9 上去了。例如 GF(2^3) 乘 计算 

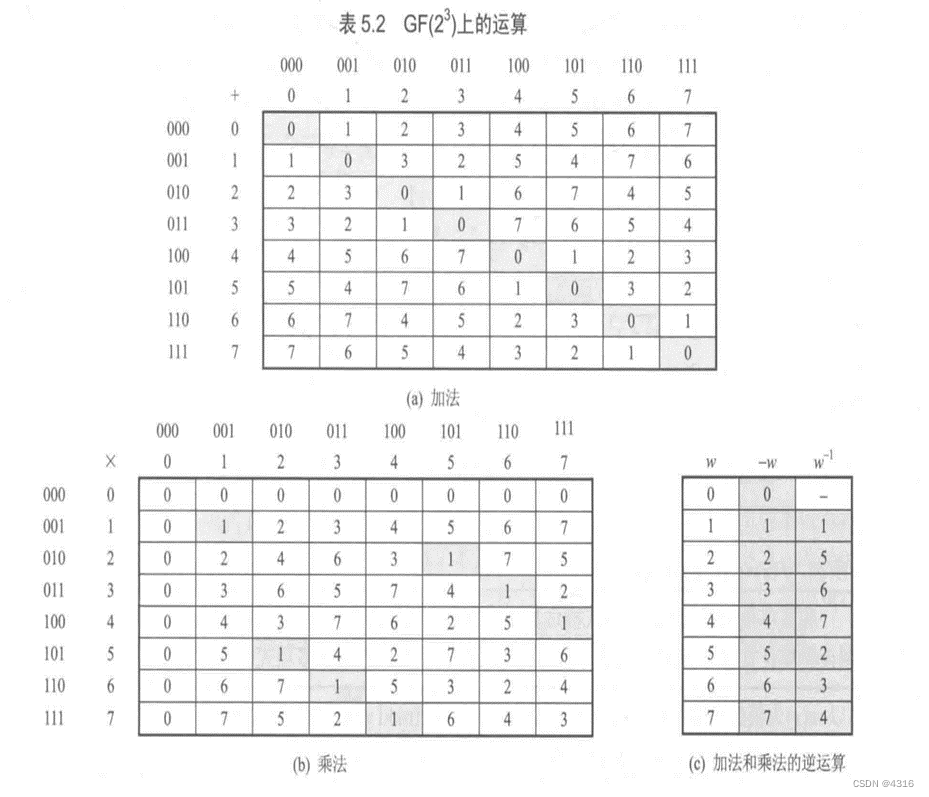
可以看到 7*4=1 但是我们计算 7*4=28 有限域的计算并非数学意义上的乘法，2^3=8 即代表最大可表示数为 111=7=8-1, 通俗的讲 就是28 3位二进制不够表示，那怎么办？取模 mod m(x)

m(x)就是不可约不等式 gf(2^3)（最高次是3）的 m(x)=x^3+x^2+1,x^3+x+1 为什么是这两个而不是其他的？

例如 x^3+x^2+x+1 , 我们将 0 和1 带入上述三个式子，最后一个在X=1时等于0，而前两个在x=1和x=0时均不为0（注意是要同时满足）这样我们称之为不可约多项式 ，好的下面我们来计算

7二进制表示为111，对应的多项式就是 x^2+x+1(注意是从（x^0 零次方开始算)

7（111） * 4（100）=(x^2+x+1) *（x^2）=x^4+x^3+x^2 最高次为4次方超过了3 对其取模

x^4+x^3+x^2 mod x^3+x+1 = 1  计算过程如下  最后的余数 就是结果1 （注意转化为相对的进制）

有限域的 加法 是 异或 ，上述还有一种情况是 两个数相乘没有超过可以最大可表示的数，那么结果当然就是乘完之后得到的数，所以有限域上的乘法 是模乘 而不是简单的乘法

最后，选择不同的不可约多项式 计算的结果可能不同