狄利克雷原理及其应用

狄利克雷原理及其应用

简介

狄利克雷原理是19世纪德国数学家狄利克雷提出的，狄利克雷原理又名鸽舍原理，抽屉原理。

原理

第一抽屉原理

原理1

把n+k（k>=1)个苹果放进n个抽屉里，则至少有一个抽屉中有2个或2个以上的苹果

证明

反证法：如果每个抽屉至多放进一个苹果，那么放入抽屉的苹果的总数至多是n*1个，而不是n+k（k>=1）个，故至少有一个抽屉中有2个或2个以上的苹果

原理2

把n*m+k（k>=1)个苹果放在n个抽屉里，则至少有一个抽屉中有m+1或m+1以上个苹果

证明

反证法：如果每个抽屉中至多放入m个苹果，那么放入抽屉的苹果总数至多是n*m个，而不是题设的n*m+k（k>=1)个苹果，故至少有一个抽屉中有m+1或m+1以上个苹果

原理3

把无数个苹果放入n个抽屉中，则至少有一个抽屉中有无数个苹果

证明

反证法：如果每个抽屉只能放有限个苹果，那么放入抽屉中的苹果也是有限个，与题设不符，故至少有一个抽屉中有无数个苹果

第二抽屉原理

原理

把n*m-1个苹果放入n个抽屉中，则必有一个抽屉中至多有m-1个苹果

证明

反证法：每个抽屉都放入n个苹果，总共有n*m个苹果，与题设不符，故必有一个抽屉中至多有m-1个苹果

应用及分析

应用1（最大间隙问题）

给定n个实数(x₁，x₂，……，x_n)，求这n个数在实轴上相邻两个数之间的最大差值。假设对任何实数的下取整函数耗时O(1)，设计解最大间隙问题的线性时间算法
$$\begin{gathered} 输入:2.33.17.51.56.3 \\ 输出:3.2 \end{gathered}$$

解析

原理：利用桶排序原理，构造n+1个桶，将数放入n+1个桶中。利用狄利克雷原理可知，一定存在一个或多个空桶。

从而可知：两个实桶中间存在空桶的地方便是可能存在最大间隙的地方

证明：

1. 先证明一定存在空桶：

(反证法)：每个桶都放一个数，数的总个数为n个，小于n+1，与题设不符，那么一定存在一个或多个空桶。

2. 在证明最大间隙存在于空桶存在的地方

   中间不存在空桶的情况：间隙 m = 后一个桶中数的最小值 - 前一个桶中数的最大值

   中间存在k（k<=n-1）个空桶的情况：间隙 n = 后一个桶中数的最小值 - 前一个桶中数的最大值 + k * 桶的大小

   m < n， 中间存在空桶的间隙会大于不存在空桶的间隙，又因为空桶不一定连续存在，存在空桶的地方都有可能是最大间隙，所以两个实桶中间存在空桶的地方便是可能存在最大间隙的地方

构造：

1. 构造 n+1 个记录桶

2. 取序列中的最大值 max 和最小值 min 作为桶的最大边界和最小边界

3. 每个桶的大小为 (max - min) / (n + 1)

4. 假设
   n = 5 序列为: 0 4 8 14 18

   max= 18， min = 0

构造如下

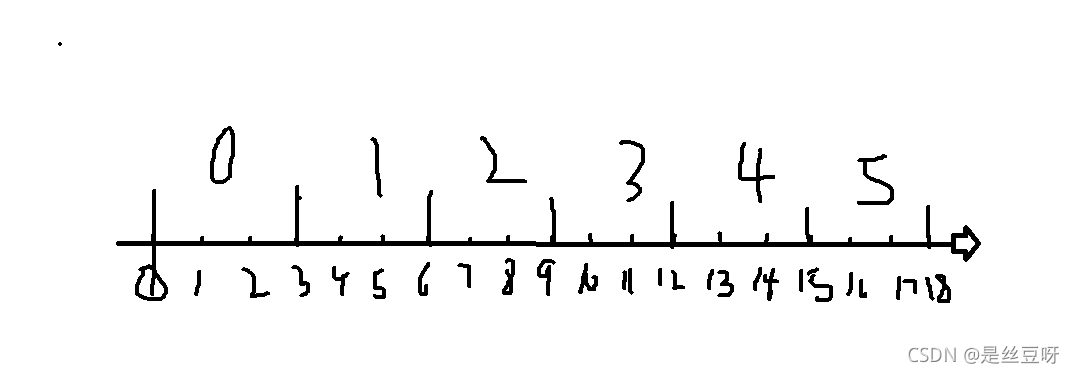
5. 将数放入桶中，桶会记录放入数的最大值和最小值
   

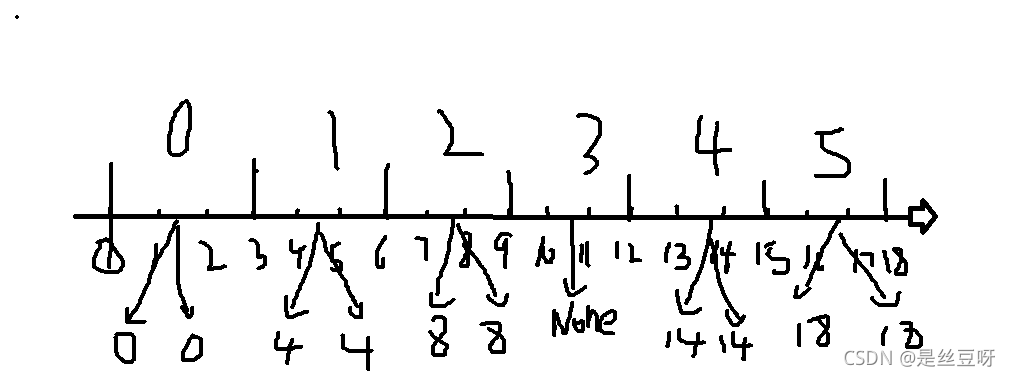
6. 先去去掉空桶，遍历一遍所有桶，用每个桶的最小值减去前一个抽屉桶的最大值，便得到了最大间隙

代码实现

'''知识储备：鸽巢原理'''
with open('input', 'w') as file:  # 写入数据
    a = int(input())
    lst = list(map(str, input().split()))
    file.write(str(a)+'\n')
    file.write(' '.join(lst)+'\n')

e = 0.001  # 鉴于会浮点数操作，定义一个判等误差e
print('output.txt')
with open('input', 'r') as file, open('output', 'w') as result:  # 打开文件
    n = int(file.readline().rstrip('\n'))  # 读取浮点数的个数
    lst = list(map(float, file.readline().split()))  # 读取第二行并切片成包含浮点数的列表
    l, r = min(lst), max(lst)  # 获取左右边界
    res = 0
    if r - l < e:  # 如果左右边界一样，那么最大间隙就是0
        pass
    else:
        bucket = [[None, None] for i in range(n+1)]  # 准备n+1个桶，至少一个桶是空的
        width = (l - r)/n  # 桶的宽度,因为最大值位于桶的边界，会进入更大的桶中，超出桶的范围，故将桶的宽度变大
        for num in lst:  # 把这些数放到n+1个桶里
            b = bucket[int((num-l)//width)]  # 确定该数在哪个桶里
            b[0] = min(b[0], num) if b[0] else num  # b[0]为该桶里最小的数
            b[1] = max(b[1], num) if b[1] else num  # b[1]为该桶里最大的数
        bucket = [b for b in bucket if b[0] is not None]  # 去掉空桶
        res = max(bucket[i][0] - bucket[i-1][1] for i in range(1, len(bucket)))  # 获的最大间隙
    result.write(str('%.1f' % res))
    print('%.1f' % res)

延伸：

桶的个数没有上限，对下限有要求。

上限就不证明了，和上面同理

• 证明当桶的个数为n-1时，实现O(n)复杂度的可行性

  存在空桶时，最大间隙依然存在与存在的空桶的地方

  当不存在空桶时，先每一个桶都放一个数，由于只有n-1个桶，所以还会多出来一个数，随便选择一个桶放入，只会改变该桶的最大值或最小值，所以遍历一遍所有抽屉，用每个抽屉的最小值减去前一个抽屉的最大值，便依然可以得到了最大间隙

• 当桶的个数为n时与桶的个数为n-1时同理

• 当桶的个数等于 n-2 时

  当存在空桶时，最大间隙依然存在与存在的空桶的地方

  但当不存在空桶时，先每个桶都放一个数，由于桶的个数等于n-2，所以会多出来两个数还未放入桶中。当n = 3时，三个数（max， mid， min）放入一个桶中时，得到的答案是max-min，而最大间隙应该是max-mid或mid-min。当n大于3时，出现空桶的情况与上相同。当不出现空桶时，多出的两个数只会改变原先桶的上下限，并不会改变最大间隙。故当桶的个数是n-2时，需满足n >= 4。

• 以此类推

  假设桶的个数是n - k，需满足 2*k <= n