素数筛 欧拉函数

最新推荐文章于 2024-07-07 10:00:00 发布
最新推荐文章于 2024-07-07 10:00:00 发布
阅读量589 收藏 2
点赞数
分类专栏： ACM 初等数论 文章标签： 算法 初等数论
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_54886579/article/details/119958593
版权

目录

参考文献

素数及其相关定理

一、素数定义 ​

基本概念

易错点

唯一分解定理

二、素数的判定

朴素算法（时间复杂度O(n)）:

进阶算法（时间复杂度O(sqrt(n))）：

三、筛法求素数

1、埃氏筛法（时间复杂度O(nloglogn)）

2.欧式筛法（时间复杂度O(n)）

欧拉函数

概念

分类讨论

第一种情况

第二种情况

第三种情况

第四种情况

第五种情况

模板

筛法求欧拉函数和素数

例题分析

欧拉降幂

欧拉定理（可略过）

扩展欧拉定理（可略过）

​欧拉降幂公式 

快速幂

欧拉降幂模板

例题

参考文献

特别鸣谢武大佬的PPT

素数筛

欧拉定理

洛谷P4139题解

筛法求欧拉函数

素数及其相关定理

一、素数定义 ​

基本概念

素数又称质数，是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。 ​

易错点

1不是质数，写题要注意出题人出0,1卡你，质数大于1

唯一分解定理

一个数n肯定能被分解成 n=p1^a1 * p2^a2 . . .*pn^an（p是素因子，a是素因子的个数）因为一个数肯定是由合数和质数构成的，合数又可以分解成质数和合数，最后递归下去就会变成质数的乘积最后化成了质数相乘的形式

二、素数的判定

朴素算法（时间复杂度O(n)）:

bool isprime(int x) {
	for(int i=2; i<=x; i++) {
		if(x%i==0) return false;
	}
	return true;
}

进阶算法（时间复杂度O(sqrt(n))）：

可以注意到如果在2~n-1中，存在n的约数，不妨设为k，即n%k==0，那么由k*(n/k)==n可知，n/k也是n的一个约数，且k与n/k中一定满足其中一个小于等于sqrt(n)、另一个大于等于sqrt(n)，其中sqrt(n)为根号n。那么只需要判定n能否2,3…sqrt(n)中的一个整除，即可判定n是否为素数。

bool isprime(int n) {
	if(n<=1) return false;
	for(int i=2; i<=sqrt(n); i++) {
		if(n%i==0) return false;
	}
	return true;
}

三、筛法求素数

1、埃氏筛法（时间复杂度O(nloglogn)）

素数筛法的关键就在于一个“筛”字。算法从小到大枚举所有数，对每一个素数，筛去它的所有倍数，剩下的即为素数。

下面以n=16为例

const int maxn=1e4+10;
int prime[maxn],pnum=0;//prime数组存放所有素数，pnum为素数个数
bool p[maxn];//如果i为素数，则p[i]为false,否则p[i]为true
void find_prime() {
	for(int i=2; i<maxn; i++) {
		if(p[i]==false) {
			prime[pnum++]=i;
			for(int j=i+i; j<maxn; j+=i) {
				//筛去i的倍数
				p[j]=true;
			}
		}
	}
}

缺点：有些数被重复筛去，比如6被2筛去，又被3筛去，造成浪费

2.欧式筛法（时间复杂度O(n)）

欧式筛法对于每个数字，总是被它的最小质因子筛掉，所以每个数字都只遍历一次，所以时间复杂度是O(n)。 首先，我们要保证每一个数字是被他的最小质因子筛掉的，那么我们遍历因子，用已经得到的素因子从小到大的去乘因子。 此时会出现两种情况：1、因子中不包含素因子，那么可以继续乘下去。2、因子中包含了素因子，那么如果因子继续乘下去，所得的积的最小质因子就是之前所包含的素因子，会出现重复筛除，所以break。

bool isnp[MAXN];//素数为0，合数为1，初始化为0
vector<int> primes; // 质数表
void init(int n) {//在主函数中别忘了调用 
	for (int i = 2; i <= n; i++) {
		if (!isnp[i])
			primes.push_back(i);
		for (int p=0; p<primes.size(); p++) {
			if (primes[p] * i > n)//越界返回
				break;
			isnp[primes[p] * i] = 1;//这一步在下一步之前，比如4*2要先把8划掉再退出 
			if (i % primes[p] == 0)//精髓 
				break;
		}
	}
}

欧拉函数

概念

任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？（比如，在1到8之中，有多少个数与8构成互质关系？）

计算这个值的方法就叫做欧拉函数，以φ(n)表示。在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(n) = 4。

分类讨论

第一种情况

如果n=1，则 φ(1) = 1 。因为1与任何数（包括自身）都构成互质关系。

互质是公约数只有1的两个整数，叫做互质整数。公约数只有1的两个自然数，叫做互质自然数，后者是前者的特殊情形。

第二种情况

如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。

第三种情况

如果n是质数的某一个次方，即 n = p^k (p为质数，k为大于等于1的整数)，则

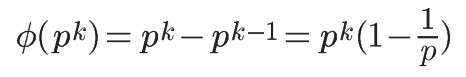
p^k也就是n,p^(k-1)也就是n/p，那么上面的式子还可以写成下面的形式：

n-\frac{n}{p}

比如 φ(8) = φ(2^3) =2^3 - 2^2 = 8 -4 = 4。

这是因为只有当一个数不包含质数p，才可能与n互质。而包含质数p的数一共有p^(k-1)个，即p、2p、3p、...、p^(k-1)×p，从1到p^(k-1)一共有p^(k-1)项，也就是n/p项，把它们去除，剩下的就是与n互质的数。

可以看出，上面的第二种情况是 k=1或者说n=p时的特例。

第四种情况

如果n可以分解成两个互质的整数之积， n = p1 × p2 则 φ(n) = φ(p1p2) = φ(p1)φ(p2)， 即积的欧拉函数等于各个因子的欧拉函数之积。

比如，φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。

这一条的证明要用到"中国剩余定理"，这里就不展开了，只简单说一下思路：如果a与p1互质(a<p1)，b与p2互质(b<p2)，c与p1p2互质(c<p1p2)，则c与数对 (a,b) 是一一对应关系。由于a的值有φ(p1)种可能，b的值有φ(p2)种可能，则数对 (a,b) 有φ(p1)φ(p2)种可能，而c的值有φ(p1p2)种可能，所以φ(p1p2)就等于φ(p1)φ(p2)。

第五种情况

也就是n/p1*(p1-1)/p2*(p2-1).../pn*(pn-1)

根据公式可以写出下列代码，注意开long long 

ll euler(ll n) {
	ll ans = n;
	for(int i=2; i*i <= n; i++) {//等于号不能丢，否则根号的质因子不会被计算，转而会把n本身计算在内
		if(n%i == 0) {
			ans = ans/i*(i-1);
			while(n%i == 0)
				n/=i;
		}
	}
	if(n > 1) ans = ans/n*(n-1);
	return ans;
}

那么，结合筛法求素数，我们可以写出下列模板

易错点：!n%t要写成!(n%t)，优先级问题

模板

#include<cstdio>
#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
const int N=1e7+10;
bool isnp[N];//素数为0，合数为1，初始化为0
vector<int> primes; // 质数表
void init() {//在主函数中别忘了调用 
	for (int i = 2; i <= N; i++) {
		if (!isnp[i])
			primes.push_back(i);
		for (int p=0; p<primes.size(); p++) {
			if (primes[p] * i > N)//越界返回
				break;
			isnp[primes[p] * i] = 1;//这一步在下一步之前，比如4*2要先把8划掉再退出 
			if (i % primes[p] == 0)//精髓 
				break;
		}
	}
}
ll euler(ll n){
	ll ans=n;
	for(int i=0;i<primes.size();i++){
		int t=primes[i];
		if(t*t>n)	break;//遍历到根号之前即可,注意不能带等号,否则根号的质因子不会被计算，反而会把n计算在内 
		if(n%t==0){
			ans=ans/t*(t-1);
			while(n%t==0)	n/=t;
		}
	}
	if(n>1)	ans=ans/n*(n-1);
	return ans;
}
int main(){
	init();
	int a,t;
	scanf("%d",&a);
	t=euler(a);
	printf("%d",t);
	return 0;
}

筛法求欧拉函数和素数

该算法在可在线性时间内筛素数的同时求出所有数的欧拉函数。

    需要用到如下性质(p为质数)：

    1. phi(p)=p-1   因为质数p除了1以外的因数只有p，故1至p的整数只有p与p不互质

    2. 如果i mod p = 0, 那么phi(i * p)=p * phi(i)  证明如下

 上面的过程证明了从区间[1,i]->[i+1,i+i]，若整数n不与i互质，n+i依然与i不互质。下面给出另一个证明：若整数n与i互质，n+i与i依然互质 

 

 3.若i mod p ≠0,  那么phi(i * p)=phi(i) * (p-1)
        i mod p 不为0且p为质数, 所以i与p互质, 那么根据欧拉函数的积性phi(i * p)=phi(i) * phi(p) 其中phi(p)=p-1即第一条性质

#include<iostream>
#include<cstdio>
const int N=1e7+10;
using namespace std;
int phi[N+10],prime[N+10],cnt;//phi是欧拉函数数组，prime是素数数组，cnt是素数下标 
bool mark[N+10];//素数筛的标记数组 
void getphi() {
	int i,j;
	phi[1]=1;//特判 
	for(i=2; i<=N; i++) { //相当于分解质因式的逆过程
		if(!mark[i]) {
			prime[++cnt]=i;//筛素数的时候首先会判断i是否是素数。
			phi[i]=i-1;//当 i 是素数时 phi[i]=i-1
		}
		for(j=1; j<=cnt; j++) {
			if(i*prime[j]>N)  break;
			mark[i*prime[j]]=1;//确定i*prime[j]不是素数
			if(i%prime[j]==0) { //接着我们会看prime[j]是否是i的约数
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			} else  phi[i*prime[j]]=phi[i]*(prime[j]-1); //其实这里prime[j]-1就是phi[prime[j]]，利用了欧拉函数的积性
		}
	}
}
int main() {
	getphi();
}

例题分析

洛谷2158

注意：体委在方阵中而不是方针外，不要被现实生活经验所迷惑（这题出的真是迷惑，我想半天没想明白输入4咋得到的9，一看题解好家伙体委在队伍内监督，人类迷惑行为） 

根据物理原理光沿直线传播，体委的目光相当于无数条光线，照射到的第一个人会被看到，同一条光线后面的人就被遮挡，看不到了。

这题等价于从原点(0,0)划分出无数条射线簇，方程为y=kx(k∈[0,+∞))和射线x=0(y≥0)，射线与点阵的第一个交点被标记为1，后续交点被标记为0，求标记和。点阵(i,j)范围i,j∈[0,n-1]且i,j∈N*

简单模拟一下，(1,2)∈y=2x，(2,4)会被(1,2)遮挡，多模拟几个点会发现当且仅当y/x=k且y和x不能被约分的时候才会被看到，不能被约分等价于gcd=1，也就是x,y互质

那好说啊，欧拉函数有用武之地

以N=4为例，我们分析(1,1)~(3,3)即可，因为（0,1）和（1,0）这两条斜率特殊的线可以预处理

1,1 1,2 1,3
2,1 2,2 2,3
3,1 3,2 3,3

我们对每一个坐标对判断x,y的gcd是否为1，是则标记1，否则标记0

1 1 1
1 0 1
1 1 0

N从1到1e4，n^2暴力肯定过不去，所以我们得简化一下，拆分横纵坐标寻找数的规律

1:1,2,3
2:1,2,3
3:1,2,3

这么拆分过于简单而且没有拆分透彻，所以无法简化运算，我们按从大到小的顺序进行九十度拆分（如下图所示）

1,1 1,2 1,3
2,1 2,2 2,3
3,1 3,2 3,3

即

3:1,1,2,2,3
2:1,1,2
1:1

我们发现，除了1之外，每个数的互质数等于每个数的欧拉函数值的二倍

那就OK了，把1也预处理掉就OK

有预处理就必须得有预打表，N=1，N=2要提前打好表，否则必WA，AC代码如下（没用筛法求欧拉函数，用的话应该更快）

#include<cstdio>
#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
const int N=1e7+10;
bool isnp[N];//素数为0，合数为1，初始化为0
vector<int> primes; // 质数表
void init() {//在主函数中别忘了调用 
	for (int i = 2; i <= N; i++) {
		if (!isnp[i])
			primes.push_back(i);
		for (int p=0; p<primes.size(); p++) {
			if (primes[p] * i > N)//越界返回
				break;
			isnp[primes[p] * i] = 1;//这一步在下一步之前，比如4*2要先把8划掉再退出 
			if (i % primes[p] == 0)//精髓 
				break;
		}
	}
}
ll euler(ll n){
	ll ans=n;
	for(int i=0;i<primes.size();i++){
		int t=primes[i];
		if(t*t>n)	break;//遍历到根号之前即可,注意不能带等号,否则根号的质因子不会被计算，反而会把n计算在内 
		if(n%t==0){
			ans=ans/t*(t-1);
			while(n%t==0)	n/=t;
		}
	}
	if(n>1)	ans=ans/n*(n-1);
	return ans;
}
int main(){
	init();
	int n,r=3;scanf("%d",&n);
	if(n==1){
		printf("0");return 0;
	}
	if(n==2){
		printf("2");return 0;
	}
	for(int i=2;i<=n-1;i++){
		r+=2*euler(i);
	}
	printf("%d",r);
	return 0;
}

欧拉降幂

欧拉定理（可略过）

初等数论想了解数学推导可以参考

推导我还真没看懂，这是因为那一行后面能划等号？离谱

扩展欧拉定理（可略过）

欧拉降幂公式 

根据上面两个定理的公式结合起来，即为下图中的欧拉降幂公式

 

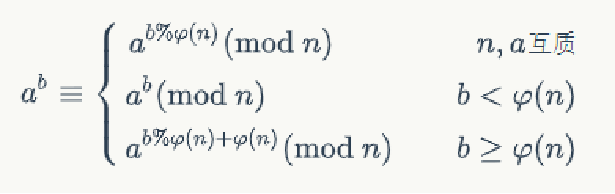
求时可以直接根据右边的条件把式子转换成上面三个中的一个 

快速幂

快速幕基于二分的思想， 因此也常称为二分幕。 快速幕基于以下事实：

1：如果 b 是奇数， 那么有 a^b = a* a^(b-1)

2：如果 b 是偶数， 那么有 a^b = a^(b/2) * a^(b/2)

显然，b是奇数的情况总可以在下一步转换为 b 是偶数的情况,而b是偶数的情况总可以在下一步转换为b/2的情况。这样，在log(b)级别次数的转换后，就可以把b变为0,而任何正整数的0次方都是1

时间复杂度O（logn）

typedef long long ll;
ll sppow(ll a,ll b,ll m) {//快速幂 求a^b%m,递归写法 如果m为1,可以直接特判为0
	if(a>=m) a%=m;//如果初始时a有可能大于等于m,那么需要在进入函数前就让a对m取模
	if(!b) return 1; //如果b为0, 那么a^0= 1
	if(b&1) return a* sppow(a,b-1,m)%m;//b为奇数，转换为b-1
	else {//b为偶数,转换为b/2
		ll t=sppow(a,b>>1,m);
		return t*t%m;
	}
}

b&1等价于b%2==1，位运算更快，！b等价于b==0

当 b%2=0 时不要返回直接返回 binaryPow(a, b / 2, m) * binaryPow(a, b / 2, m), 而应当算出单个 binaryPow(a, b / 2, m)之后再乘起来。 这是因为前者每次都会调用两个binaryPow 函数，导致复杂度变成 O(2^iog(b)) = O(b)。

例如求 binaryPow(8)时，会变成 binaryPow(4)* binaryPow(4), 而这两个 binaryPow(4)都会各自变成 binaryPow(2) * binaryPow(2), 是就需要求四次 binaryPow(2); 而每个 binaryPow(2)又会变成 binaryPow(l) * binaryPow(l), 因此最后需要求八次 binaryPow(I)。

注意：

如果m为 1, 可以直接在函数外部特判为 0, 不需要进入函数来计算（因为任何正整数对 1 取模一定等于 0)。

欧拉降幂模板

#include<iostream>
#include<cstdio>
const int N=1e7+10;
using namespace std;
typedef long long ll;
int phi[N+10],prime[N+10],cnt;//phi是欧拉函数数组，prime是素数数组，cnt是素数下标 
bool mark[N+10];//素数筛的标记数组 
void getphi() {
	int i,j;
	phi[1]=1;//特判 
	for(i=2; i<=N; i++) { //相当于分解质因式的逆过程
		if(!mark[i]) {
			prime[++cnt]=i;//筛素数的时候首先会判断i是否是素数。
			phi[i]=i-1;//当 i 是素数时 phi[i]=i-1
		}
		for(j=1; j<=cnt; j++) {
			if(i*prime[j]>N)  break;
			mark[i*prime[j]]=1;//确定i*prime[j]不是素数
			if(i%prime[j]==0) { //接着我们会看prime[j]是否是i的约数
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			} else  phi[i*prime[j]]=phi[i]*(prime[j]-1); //其实这里prime[j]-1就是phi[prime[j]]，利用了欧拉函数的积性
		}
	}
}
ll sppow(ll a,ll b,ll m) {//快速幂 求a^b%m,递归写法 如果m为1,可以直接特判为0
	if(a>=m) a%=m;//如果初始时a有可能大于等于m,那么需要在进入函数前就让a对m取模
	if(!b) return 1; //如果b为0, 那么a^0= 1
	if(b&1) return a* sppow(a,b-1,m)%m;//b为奇数，转换为b-1
	else {//b为偶数,转换为b/2
		ll t=sppow(a,b>>1,m);
		return t*t%m;
	}
}
ll gcd(ll a,ll b) {
	return b==0?a:gcd(b,a%b);
}
ll eulerpow(ll a,ll b,ll n) {//欧拉降幂公式求a^b%n 如果n==1 可直接特判为0 
	if(gcd(a,n)==1) {
		b%=phi[n];
		return eulerpow(a,b,n);
	} else {
		int t=phi[n];
		if(b<t)	return sppow(a,b,n);
		else{
			b=b%t+t;
			return eulerpow(a,b,n);
		}
	}
}
int main() {
	return 0;
}

例题

洛谷4139

不开long long过不去

求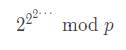

2的无限个2次方模p

那么很明显，这题的关键是把无限次方化掉

f(p)这个函数实在是太美了，理性与感性的完美统一

这个函数很容易实现

ll f(ll p) {
	return (p==1)?0:(sppow(2,f(phi[p])+phi[p],p));
}

sppow就是快速幂

#include<iostream>
#include<cstdio>
const int N=1e7+10;
using namespace std;
typedef long long ll;
int phi[N+10],prime[N+10],cnt;//phi是欧拉函数数组，prime是素数数组，cnt是素数下标
bool mark[N+10];//素数筛的标记数组
void getphi() {
	int i,j;
	phi[1]=1;//特判
	for(i=2; i<=N; i++) { //相当于分解质因式的逆过程
		if(!mark[i]) {
			prime[++cnt]=i;//筛素数的时候首先会判断i是否是素数。
			phi[i]=i-1;//当 i 是素数时 phi[i]=i-1
		}
		for(j=1; j<=cnt; j++) {
			if(i*prime[j]>N)  break;
			mark[i*prime[j]]=1;//确定i*prime[j]不是素数
			if(i%prime[j]==0) { //接着我们会看prime[j]是否是i的约数
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			} else  phi[i*prime[j]]=phi[i]*(prime[j]-1); //其实这里prime[j]-1就是phi[prime[j]]，利用了欧拉函数的积性
		}
	}
}
ll sppow(ll a,ll b,ll m) {//快速幂 求a^b%m,递归写法 如果m为1,可以直接特判为0
	if(a>=m) a%=m;//如果初始时a有可能大于等于m,那么需要在进入函数前就让a对m取模
	if(!b) return 1; //如果b为0, 那么a^0= 1
	if(b&1) return a* sppow(a,b-1,m)%m;//b为奇数，转换为b-1
	else {//b为偶数,转换为b/2
		ll t=sppow(a,b>>1,m);
		return t*t%m;
	}
}
ll f(ll p) {
	return (p==1)?0:(sppow(2,f(phi[p])+phi[p],p));
}
int main() {
	getphi();
	int n,t;
	scanf("%d",&n);
	while(n--) scanf("%d",&t),printf("%d\n",f(t));
	return 0;
}

最后还是要感叹解函数的美

明月千里赴迢遥
关注
  • 0
    点赞
  • 踩
  • 2
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
【数论】【素数】素数相关基础——欧拉函数与欧拉定理
Lorry酱的专栏
07-15 2427
1、 欧拉函数   欧拉函数 φ(n)表示不超过n且与n互素的正整数的个数 。 φ(n)=n*(1-1/p1)*(1-1/p2)*…其中p1,p2…为n的质因数 2、欧拉定理 若a,n是正整数，且a,n互质，则有a^ φ(n) mod n =1。实际上这是费马小定理的一个推广。 3、欧拉函数打表 在实际运用中，用朴素方法去一次次求欧拉函数的值是很慢的，所以我们可以采用打表的方法来提高效率
线性筛素数与欧拉函数
Micro_grass的博客
06-28 403
对于筛素数问题（即给定一个整数N，求出1～N之间的所有质数，称为质数的筛选问题），我们有一些朴素的算法，比如说枚举法（时间复杂度很高，不推荐），以及埃拉特斯特尼筛法（时间复杂度为O(n loglog n），效率接近线性，但是n过大时会TLE），现在我还有两种筛法，一种是快速线性筛（时间复杂度为O(N)），还有一种是我一年前写出来的（也可能是从哪个题解里看的）玄学算法，在洛谷实测比快速线性筛快（原因...
第二十五章 数论——约数
Turing_Sheep的博客
12-25 707
详细讲解约数相关算法的证明，同时详解欧几里德算法的证明。
欧拉函数学习
STOP
02-23 231
欧拉函数用希腊字母φ表示,φ(N)表示N的欧拉函数.欧拉函数的一些性质:1.对于素数p, φ(p)=p-1，对于对两个素数p,q φ（pq）=pq-12.对于一个正整数N的素数幂分解N=P1^q1*P2^q2*...*Pn^qn.   φ(N)=N*(1-1/P1)*(1-1/P2)*...*(1-1/Pn).3.除了N=2,φ(N)都是偶数.4.设N为正整数,∑φ(d)=N (d|N).那么我们...
素数的有关性质（二）欧拉函数的一些定理证明与计算
zorchp
08-24 2827
欧拉函数的一些定理及证明，计算方法总结。
LightOJ - 1007
m0_53807008的博客
06-02 201
题目：给你t个样例 每个样例给你两个数 问你两个数欧拉数的平方的差值 思路： 就是欧拉函数打表 这里要注意欧拉函数三个性质就可以了 1.如果p是素数，那么它的欧拉值为p-1 2.φ(mn)=φ(m)φ(n)（m,n互质） 3.若i%p==0，有φ(ip)=pφi(i) 就可以打表打出来欧拉函数了 最后注意一下前缀和和开unsign long long 就好了 #include <iostream> # include <cstdio> #include <string.h&gt
欧拉函数o(n)求素数
sun897949163的博客
03-30 3311
欧拉函数的定义: E（N）= ( 区间[1,N-1] 中与 N 互质的整数个数).　　对于 积性函数 F（X*Y），当且仅当 GCD（X，Y）= 1 时， F（X*Y） = F（X）* F（Y）　　任意整数可因式分解为如下形式：　　　 其中( p1, p2 … pk 为质数, ei 为次数 )　 　　所以　　　　　　因为 欧拉函数 E（X）为积性函数， 所以　　　　 　　对于 ， 我
线性素筛 欧拉函数 区间筛素数.zip_sowoc_算法 欧拉函数 线性筛
09-24
总的来说，"线性素筛 欧拉函数 区间筛素数.zip_sowoc_算法 欧拉函数 线性筛"这个压缩包文件包含了一种高效的算法实现，该算法能够在线性时间内筛选素数，并且能快速计算欧拉函数值，适用于需要处理大量素数和欧拉...
hdu 1695 GCD（欧拉函数+容斥原理）.docx
10-29
"hdu 1695 GCD（欧拉函数+容斥原理）" 题目大意是：给定 a, b, c, d, k，找到一队 x, y，满足 g(x, y) = k，且 x ∈ [1...这道题目考察了欧拉函数、容斥原理和筛法等数论知识，并且需要使用编程技巧来实现高效的计算。
Euler函数前缀
07-06
总结来说，"欧拉函数前缀"是一个在数学和计算机科学中涉及数论和算法的重要概念，它涉及到欧拉函数的性质、计算以及在实际编程问题中的应用。理解和掌握这一知识点，不仅有助于解决竞赛编程问题，还能为深入学习数论...
Java实现欧拉筛与花里胡哨求质数高级大法的对比
12-22
代码中，`getPrime`函数实现了欧拉筛法，通过一个辅助数组`list`记录每个数是否已被处理，`prime`数组存储找到的质数。这种方法效率较高，因为它减少了不必要的计算。 接下来，描述中的“花里胡哨求质数高级大法”...
素数生成器素数生成器.zip
10-07
2. 哈希函数：某些哈希函数的设计需要用到素数，以保证散列的均匀性和随机性。 3. 数据结构：素数在构建哈希表、B树等数据结构中也有应用。 四、素数生成器的实际应用 1. 教育教学：在数学教学中，素数生成器可以...
欧拉函数的求法（三种）
bibohaohao的博客
03-23 3876
欧拉函数定义 求欧拉函数的方法 1.公式法 2.线性筛法 根据三条性质来解题的： //1、当p为质数的时候：phi(p)=p-1 //2、当p与i互质时有: phi(p*i)=phi(p)*phi(i) //3、当i%p==0时有：phi(p*i)=p*phi(i) 具体实现参考链接： 1.求欧拉函数的三种常见类型及解决代码 2.求欧拉函数的代码 ...
素数筛（埃氏筛、欧拉筛）
m0_54123999的博客
08-02 4191
那么对于任意的i>2，当我们遍历到i时，则我们一定先遍历了[2,i-1]之间的所有数，若isprime[i]为false，则证明i不是[2,i-1]中任意素数的倍数，即i只能被1和它自身整除，所以i为素数。若x∈[2,i-1]，则x*i一定已经被标记为合数了，因为在遍历到i之前，我们一定已经遍历过x了，若x的最小质因数为k，k*y==x，则x的i倍即k的i*y倍若小于n则一定已经被标记过了。那么问题来了，如果我给你一个数字n，让你判断有多少个小于n的素数，...
素数：欧拉筛法（自己的一些认识）
蓝展展的博客
08-10 4273
对于原创：https://blog.csdn.net/Losk_0/article/details/87884390的一些认识 转自：https://blog.csdn.net/Losk_0/article/details/87884390 简单就是说：当i == 4 时， 4 * 2 = 8， 将8筛掉是可以的 4 * 3 = 12 是不可以的 因为 4 % 2 == 0 所以 4 = 2 * 某个数n（此处n = 2） 所以可以写成 2 * 2 * 3 = 12； 所以 2 * 6 = 12 12将会
素数筛，欧拉函数
qq_55788328的博客
08-27 777
素数筛: 1.埃氏筛法（时间复杂度O(nloglogn)） const int maxn=1e4+10; int prime[maxn],pnum=0;//prime数组存放所有素数，pnum为素数个数 bool p[maxn];//如果i为素数，则p[i]为false,否则p[i]为true void find_prime(){ for(int i=2;i<maxn;i++){ if(p[i]==false){ prime[pnum++]=i; for(int j=i+i
判断素数----欧拉筛选法
gaoqiandr的博客
09-15 1409
对于判断素数的欧拉筛法的解释，简单易懂，适合小白同学
数据结构与算法：欧拉筛——查找素数（质数）的最优解算法 O(n)
Sea3752的博客
05-04 3661
欧拉筛——查找素数（质数）的最优解算法
【排序算法】插入排序（希尔排序）
最新发布
2301_80555259的博客
07-07 666
直接插入排序是一种简单的插入排序法，其核心思想是对一个已经有序的序列插入一个数据，该数据依次比较有序序列中的值，直到插入到合适的位置。在我们玩扑克牌整理牌序的时候，用到的就是直接插入排序的思想。
python欧拉筛法求素数
05-24
欧拉筛法是求解素数的一种高效算法，它的基本思想是通过筛去合数来得到素数。下面是Python实现欧拉筛法求素数的示例代码： ```python def euler_sieve(n): primes = [] is_prime = [True] * (n + 1) for i in ...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值