引言
本文记录了对Link16同步技术的复现过程,使用软件是MATLAB,主要是完成了Link16同步头数据的产生,同时通过非相关的方法完成了Link16的同步,主要是以32倍下采样完成粗同步,1倍下采样完成了精同步。
同步传输波形
在Link16系统中,一共有32个粗同步头和8个精同步头,每个同步头的长度为32。本文主要选择传统Link16链路中用于扩频的循环码移键控(Cyclic Code Shift Keying,CCSK)序列。该序列具有良好的自相关性和互相关性,在数据链中主要用作扩频码,码元与码字的对应如下表所示。
表1 码元与CCSK对应表

在调制方面,同步序列采用MSK调制进行发送,表达式为:
式中,为信号的幅度,
表示载波的频率,
为发送的信息比特,
,
为信号的符号周期,
表示前
个符号的相位累积,由前后信息比特的差值决定,表达式为:
由上式可知,MSK信号具有连续相位、恒包络等特点。与常用矩形成型的二进制相移键控(Binary Phase Shift Keying,BPSK)信号相比,MSK信号占用带宽小、频谱利用率高且容易放大发送。更为重要的是,同步序列采用MSK调制发送能保证整体信号频谱的一致性,从而提升系统的抗截获性能。
跳频图案
基带MSK信号经过射频发送后工作在960MHz~1215MHz频段上,一共有51个频点,跳频带宽即为237MHz,每个频点的间隔为3MHz。由此可见系统的跳频频点足够多且跳频范围,能有效避免频带阻塞式干扰和瞄准式干扰。本系统中每个单脉冲对应着一个跳频频点,载波驻留期为13us,跳频速率可达76923次/s,可有效地躲避跟踪式干扰。
载波频率随机跳变的规律称之为跳频图案。在跳频图案的构造上,往往遵循平衡性和宽间隔性。平衡性是指在一个跳频周期中各个频率出现的次数要尽可能一致;宽间隔性是指相邻跳频频点的频率差尽可能大,这有助于提升系统的抗衰落和抗干扰能力。
遵循以上原则,在本系统中,粗同步头和精同步头的跳频图案中包含八个不同的跳频频点。对于粗同步头,需要利用八个不同的频点组成包含32个频点的跳频图案。为了后续进行捕获算法设计,可将粗同步分为四组,每组八个同步头,每个同步头对应不同的跳频频点,并且各组之间的频点顺序无明确规律性。对于精同步头的跳频图案,每个同步头对应着一个跳频频点。与此同时,跳频图案中相邻跳频频点的间隔不小于30MHz。
同步整体方案设计
由系统链路仿真结果可知,为了防止定时偏差对链路性能造成的损失过大,在高斯信道下,当时,同步定时位置在理想位置前后
内的概率需要大于99%。同时在衰落信道下,需要在
dB时满足定时精度。此外,链路本身的抗频偏性满足指标需求,并考虑实现资源,暂不设计频偏估计。
为了方便接收的相关运算,在发送端,我们选择一组m序列,经MSK调制后形成基带波形。在跳频方面,在数字域中完成对信号的跳频后,再经过射频发送至工作频段。
为了减小运算的复杂度,我们将粗同步头和精同步头分别处理,即粗同步头完成同步捕获,精同步头完成精确定时。再粗同步捕获过程中,以一个比较大的采样倍数对接收信号进行下采后,与本地同步序列作相关运算,使粗同步的定时精度控制在符号量级内。在精同步定时估计中,则以一个比较小的采样倍数对接收信号进行下采后作相关运算,将定时精度控制在采样点量级内,完成最终的定时,以此减小资源开销。此外,捕获算法需要八路并行完成信号的下变频及相关运算,而在精同步运算过程中,已经确定出了精同步头的大致位置,可以串行对信号进行解跳,即只需一路就能完成精同步的跳频接收。
在门限判决方面,粗同步一共有32个同步头,可利用相关峰值之间的对应位置来进行判决,即多相关峰值位置判决发,以此降低传统门限设置法的繁杂性。对于精同步,当接收信号与本地序列对齐时,得出的相关值最大,即可利用区间求最值的方法来完成定时估计。
综上可得出同步处理关键流程,首先将同步序列进行MSK调制,与报头和业务信号一起组帧,组帧完成后跳频发出。接收端对信道传来的信号进行同步捕获(粗同步)计算,即先进行八路并行接收,然后进行相关运算,得出每路的相关值,最后利用多相关峰值进行门限判决,如果判决失败就继续搜索,判决成功则根据捕获位置取出精同步数据,进行定时估计(精同步)运算。精同步运算主要包括串行解跳、相关运算及最值判决,以此将定时精度缩小到采样点量级范围内,给出定时位置,完成最终的定时。

图1 同步处理的关键流程
同步捕获算法的设计
分析Link-16系统的数学模型,接收端的接收信号经正确下变频及滤波后为:
其中,为经正确下变频及滤波后的接收信号;
为扩频码
经过基带MSK调制得到的复基带信号,即同步头,满足
;
为时延;
为频偏,
表示第
个单脉冲由于器件不稳定所产生的随机相偏,在
范围内服从均匀分布;
是均值为零,方差为
的加性高斯白噪声。
假设采样速率为,则采样周期
,采样后的接收信号为:
其中,对应
这个采样时刻的采样点,
为时延所对应的采样点数。
基于匹配滤波法设计的同步系统的关键任务是,计算及处理接收信号和本地信号之间的相关值。理想情况下,当接收信号与本地信号匹配时,相关值就会出现一个很明显的尖峰,通常称为相关峰,通过寻找相关峰的位置来找到帧起始的位置。但是,由于信道噪声、频偏、相偏以及其他因素的影响,会使相关峰变得模糊甚至无法分辨。因此,必须对其进行进一步的处理,来提高其分辨性。
在本节中,将同步算法分为相关值计算、相关值处理以及检测和判决三个步骤。
a.第一步是将接收信号与本地同步头相关。
接收信号首先与本地已调扩频MSK信号共轭相乘得到,具体表示为:
然后对进行累积、平均,得到
其中,为第
个单脉冲所对应的相关值;
是一个相干累积周期内的信号采样点数,一个单脉冲同步头有32个符号,若每个符号的采样点数为
,则满足
,结合同步头格式可知,一个单脉冲的采样点数能使
,
,...,
包含一个扩频码
周期的MSK调制信号。
当接收信号与本地同步头对准时,第个单脉冲同步头内采样点
、
的相关值
为:
其中,,满足
;
是一个复信号,
、
分别为
的实部和虚部,具体表示为:
当接收信号没有与本地同步头对准时,仿照以上步骤得到相关值的虚部
、实部
也服从正态分布,具体如下:
第二步将对相关值进行处理,去除接收信号中载波相位和噪声的影响。最常用的去除载波相位的方法是对相关值进行平方处理。
当接收信号与本地同步头对准时,相关值经过平方率检波器的输出
为:

图2 8路平方处理后的相关值
Link-16链路的粗同步发送在8个频点上,按照匹配滤波发接收端也将在8个频点上进行接收,将8路相关值经过平方率检波器输出。当信道没有噪声时,能够更清晰的看到8路输出的情况,如上图所示,可以看到,由于32个单脉冲粗同步头随机发送在8个频点上,因此每个频点有4个相关峰。但是,由于信道噪声、频偏、相偏以及其他因素的影响,会使相关值变得模糊甚至无法分辨。因此,必须对其进行进一步的处理。考虑将多个相关峰延迟叠加,以提高其可分辨性,得到最终的非相干累积至作为判决统计量:
粗同步时考虑在32个单脉冲粗同步头长度范围内,根据跳频图案将每一路对应的4个相关峰均延迟至第32个相关峰的位置,并进行叠加得到最终的判决统计量,为了进行区分,将第路的判决统计量称为
。
第三步对相关峰采用合理的方式进行检测及判决。
可以采用固定门限法、恒虚警发及最大值法进行检测。
仿真实验
参数设置
参数设置,我们设置符号速率为5MBaud,系统的采样率为160MHz,调制方式为MSK,粗同步头的个数为32,精同步头的个数为8个。
结果展示
1.同步头的时域波形如图所示。
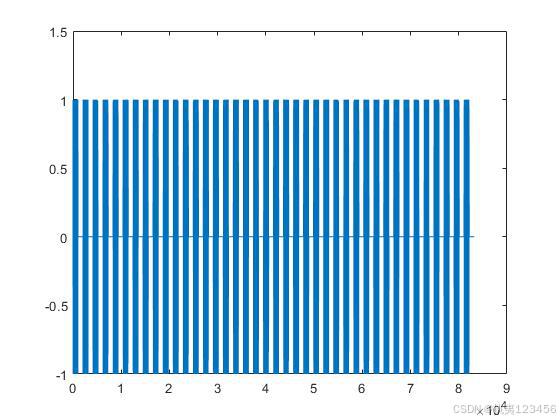
如上图所示,共有40个同步头,其中有32个粗同步头,8个精同步头。
2.32个粗同步头的相关峰如图所示。
























 2556
2556

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








