SVM理论篇-小白也能看懂的机器学习算法

本教程 基于周志华老师的《机器学习》来写的，基于自己的理解和自己举的一些小例子，希望小白可以快速学习和理解机器学习算法。PPT和相关代码可以在评论区留下邮箱，会自动发送到邮箱内。

点个赞吧请你吃欧润据~

SVM

基础概念

核心思想

在特征空间中找到一个最优超平面，将两类样本分开，并最大化分类间隔（Margin），以提高模型的泛化能力。

间隔最大化的直观类比

以道路中间画分界线为例，形象地说明间隔最大化就如同让道路两边的车辆离分界线越远越好。这样即使有新的车辆（新样本）加入，也不容易分错车道（分类错误），从而提高了模型的泛化能力。

超平面选择对泛化能力的影响

在特征空间中，不同的超平面对于样本分类的效果不同。合适的超平面能够使新样本被准确分类，而不合适的超平面可能导致分类错误。

线性可分SVM

线性可分的数学定义

二维空间的线性可分

在二维平面上，两类不同颜色的点可以被一条直线分开，这条直线就是超平面。

三维空间的线性可分

在三维空间中，超平面是一个平面。

高维空间的线性可分推广

虽然高维空间难以直观想象，但线性可分的概念可以从二维、三维空间推广而来。在高维特征空间中，只要存在一个n-1维的超平面能够将两类样本点完全分开，就称这些样本是线性可分的。（W可以理解为X的权重）

间隔最大化

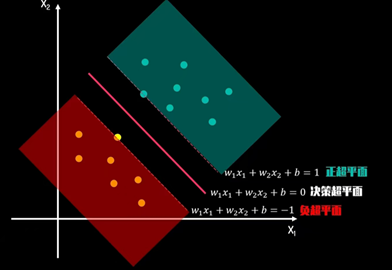
寻找最佳决策测边界线的问题可以转化为求解两类数据的最大间隔问题。间隔正中就是决策边界

寻找最佳决策测边界线的问题可以转化为求解两类数据的最大间隔问题。

间隔正中就是决策边界通过决策超平面进行分类位于正超平面的是正类，位于负超平面的是负类

间隔最大化的数学推导流程

点到超平面的距离公式：

 

软间隔

当出现了这样一个异常点是否需要为这一个异常值而牺牲间隔距离？

软间隔具有一定的容错率，目的是在间隔距离和错误大小之间寻找一个平衡

正则化参数C

不同C值下分类边界变化

当C值较大时，如 (C = 100) ，模型对违反间隔约束的容忍度较低，会尽量正确分类所有数据点，分类边界会更复杂，可能会过度拟合训练数据。当C值较小时，如 (C = 0.01) ，模型对违反间隔约束的容忍度较高，更注重最大化间隔，分类边界相对简单，可能会出现欠拟合。

过拟合与欠拟合的平衡

过拟合时模型在训练集上表现很好，但在测试集上表现不佳；欠拟合则是模型在训练集和测试集上的表现都不理想。通过调整C值，可以在过拟合和欠拟合之间找到一个平衡点，使模型在不同数据集上都有较好的泛化能力。

如果有哪里讲的不明白可以在评论区讨论 需要ppt的可以留下邮箱 到时候会发给你

封面