线性支持向量积实战篇-小白也能看懂的机器学习算法

本教程 基于周志华老师的《机器学习》来写的，基于自己的理解和自己举的一些小例子，希望小白可以快速学习和理解机器学习算法。数据集和相关代码可以在评论区留下邮箱，会自动发送到邮箱内。

线性支持向量积实战篇

iris数据集以鸢尾花的特征作为数据来源，由3种不同类型的鸢尾花的50个样本数据构成。

该数据集包含了4个属性：

Sepal.Length（花萼长度）

Sepal.Width（花萼宽度）

Petal.Length（花瓣长度）

Petal.Width（花瓣宽度）

种类：Iris Setosa（山鸢尾）、Iris Versicolour（杂色鸢尾），以及Iris Virginica（维吉尼亚鸢尾）。从sklearn.datasets导入iris数据集，利用SVM对生物物种进行分类。

一、引言

在机器学习领域，鸢尾花 (Iris) 数据集是一个经典的分类数据集，常被用于各种分类算法的入门示例。本教程将带领你使用支持向量机 (SVM) 算法对鸢尾花种类进行分类，从数据加载到模型评估，完整展示机器学习的工作流程。

二、准备工作

在开始之前，确保你已经安装了以下 Python 库：

numpy：用于数值计算

matplotlib：用于数据可视化

scikit-learn：包含机器学习算法和工具

seaborn：用于高级数据可视化

pip install numpy matplotlib scikit-learn seaborn

代码详解

首先，我们从 scikit-learn 中加载 Iris 数据集，并查看其基本信息：

# 加载Iris数据集
iris = datasets.load_iris()
X = iris.data  # 特征数据 (4个属性)
y = iris.target  # 标签数据 (3个类别)
feature_names = iris.feature_names  # 特征名称
target_names = iris.target_names  # 类别名称

print(f"数据集特征: {feature_names}")
print(f"数据集类别: {target_names}")
print(f"样本数量: {X.shape[0]}, 特征维度: {X.shape[1]}")

Iris 数据集包含 150 个样本，每个样本有 4 个特征：花萼长度、花萼宽度、花瓣长度和花瓣宽度，以及 3 个类别：山鸢尾、杂色鸢尾和维吉尼亚鸢尾。

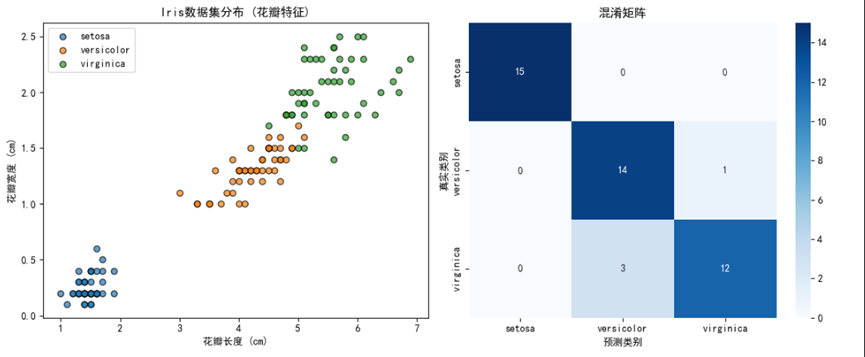
2. 数据可视化

# 数据可视化 (选取花瓣长度和宽度作为示例)
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
for i, target_name in enumerate(target_names):
    plt.scatter(
        X[y == i, 2],  # 花瓣长度
        X[y == i, 3],  # 花瓣宽度
        label=target_name,
        alpha=0.7,
        edgecolors='k'
    )
plt.xlabel('花瓣长度 (cm)')
plt.ylabel('花瓣宽度 (cm)')
plt.title('Iris数据集分布 (花瓣特征)')
plt.legend()

这里我们选择花瓣长度和宽度两个特征进行可视化，可以看到不同种类的鸢尾花在这两个特征上的分布情况，有助于我们理解后续的分类结果。

3. 数据预处理：划分训练集和测试集

接下来，我们需要将数据集划分为训练集和测试集：

# 划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42, stratify=y
)
test_size=0.3：将 30% 的数据作为测试集，70% 作为训练集
random_state=42：设置随机种子，确保结果可重现
stratify=y：分层抽样，确保训练集和测试集中各类别的比例与原始数据集一致

4. 数据预处理：特征标准化

# 特征标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

StandardScaler会将特征缩放到均值为 0，标准差为 1 的范围，这有助于 SVM 算法更好地找到最优决策边界。

5. 模型训练：网格搜索优化超参数

SVM 有多个重要的超参数，我们使用网格搜索来找到最优组合：

# 使用网格搜索优化SVM超参数
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': [0.001, 0.01, 0.1, 1],
    'kernel': ['rbf', 'linear', 'poly', 'sigmoid']
}

grid_search = GridSearchCV(
    estimator=SVC(probability=True),  # 启用概率估计
    param_grid=param_grid,
    cv=5,
    n_jobs=-1,
    verbose=1
)

grid_search.fit(X_train_scaled, y_train)

# 获取最优模型
best_svm = grid_search.best_estimator_
print("\n最优超参数：", grid_search.best_params_)

主要超参数解释：

C：正则化参数，控制误分类的惩罚力度

gamma：核函数系数，控制决策边界的复杂度

kernel：核函数类型，这里尝试了四种不同的核函数

GridSearchCV会自动尝试所有超参数组合，使用 5 折交叉验证评估每种组合的性能，最终选择最优的模型。

6. 模型评估

训练好模型后，我们需要评估其性能：

# 预测与评估
y_pred = best_svm.predict(X_test_scaled)
y_pred_proba = best_svm.predict_proba(X_test_scaled)  # 获取概率预测结果

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"\n测试集准确率：{accuracy:.4f}")

# 分类报告
print("\n分类报告：")
print(classification_report(y_test, y_pred, target_names=target_names))

# 绘制混淆矩阵
cm = confusion_matrix(y_test, y_pred)
plt.subplot(1, 2, 2)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',
            xticklabels=target_names, yticklabels=target_names)
plt.xlabel('预测类别')
plt.ylabel('真实类别')
plt.title('混淆矩阵')
plt.tight_layout()
plt.show()

我们使用了三种评估方法：

准确率：整体分类正确率

分类报告：包含精确率、召回率和 F1 分数，详细评估每个类别的分类效果

混淆矩阵：可视化不同类别之间的混淆情况

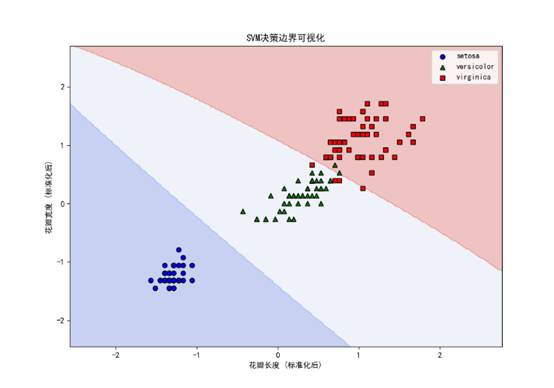
7. 决策边界可视化

为了更直观地理解 SVM 的分类原理，我们可视化其决策边界：

# 可视化决策边界 (仅展示两个特征)
# 为简化可视化，仅使用花瓣长度和宽度两个特征
X_vis = X[:, [2, 3]]  # 花瓣长度和宽度
scaler_vis = StandardScaler()
X_vis_scaled = scaler_vis.fit_transform(X_vis)

# 使用相同的超参数训练一个新的SVM模型
svm_vis = SVC(
    C=best_svm.C,
    kernel=best_svm.kernel,
    gamma=best_svm.gamma,
    probability=True
)
svm_vis.fit(X_vis_scaled, y)

# 创建网格以绘制决策边界
h = 0.02  # 网格步长
x_min, x_max = X_vis_scaled[:, 0].min() - 1, X_vis_scaled[:, 0].max() + 1
y_min, y_max = X_vis_scaled[:, 1].min() - 1, X_vis_scaled[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

# 预测网格点的类别
Z = svm_vis.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 可视化决策边界
plt.figure(figsize=(10, 7))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm)
plt.scatter(X_vis_scaled[y == 0, 0], X_vis_scaled[y == 0, 1],
            c='blue', marker='o', edgecolors='k', label=target_names[0])
plt.scatter(X_vis_scaled[y == 1, 0], X_vis_scaled[y == 1, 1],
            c='green', marker='^', edgecolors='k', label=target_names[1])
plt.scatter(X_vis_scaled[y == 2, 0], X_vis_scaled[y == 2, 1],
            c='red', marker='s', edgecolors='k', label=target_names[2])

plt.xlabel('花瓣长度 (标准化后)')
plt.ylabel('花瓣宽度 (标准化后)')
plt.title('SVM决策边界可视化')
plt.legend()
plt.show()

8. 预测示例

最后，我们展示一些具体的预测示例，看看模型是如何对新样本进行分类的：

# 输出一些预测示例
print("\n预测示例 (前5个测试样本):")
for i in range(5):
    print(f"\n样本 {i + 1}:")
    print(f"真实类别: {target_names[y_test[i]]}")
    print(f"预测类别: {target_names[y_pred[i]]}")
    print(f"预测概率: {y_pred_proba[i].max():.4f}")
print(f"特征值: {X_test[i]}")