朴素贝叶斯-小白也可以看懂的机器学习算法

最新推荐文章于 2025-05-27 23:10:16 发布

加把劲骑士16

最新推荐文章于 2025-05-27 23:10:16 发布

阅读量1.2k

点赞数 54

文章标签：机器学习

本文链接：https://blog.csdn.net/qq_56622605/article/details/148206589

版权

本教程基于周志华老师的《机器学习》来写的，基于自己的理解和自己举的一些小例子，希望小白可以快速学习和理解机器学习算法。PPT和相关代码放到评论区了需要自取。

贝叶斯决策论

贝叶斯决策论（Bayesian decision theory）是在概率框架下实施决策的基本方法。

核心在于利用已知的概率信息（先验概率、后验概率等）以及误判损失，来选择最优的决策方案，也就是最优的类别标记。

在这先补充一下先验概率、后验概率的基本概念：

先验概率

指在不考虑任何新信息（样本数据）的情况下，根据以往经验或常识，对事件发生可能性的一个预先估计。它是一种基于总体情况的概率，不依赖于当前所研究的具体样本的特征。

例如：抛硬币：已知一枚质地均匀的硬币，抛一次正面朝上的概率是0.5。这个0.5就是在抛硬币之前，基于硬币本身的属性（均匀）得到的先验概率，在还未进行实际抛掷操作时就已经确定。

后验概率

后验概率是在考虑了新的信息（样本数据）之后，事件发生的概率。它是通过将先验概率与新信息所提供的证据相结合，利用贝叶斯公式计算得出的概率，反映了在特定样本特征下事件发生的可能性。

以高考举一个简单的例子：

假设在每年有100万考生参加高考，根据以往数据统计，考上一本院校的考生占比为10%，这就是考上一本的先验概率。

有一位考生小李，他在高中三年的学习中，成绩一直处于年级前5%，平时模拟考试的成绩也都在一本线以上。根据学校历年的升学情况，成绩处于年级前5%且模拟考试达一本线以上的学生，最终考上一本院校的比例为80%。这就是结合了小李具体学习情况后的后验概率。

这里的后验概率80%，相较于先验概率10%，更能准确地反映出小李考上一本院校的可能性。因为它考虑了小李个人的成绩信息这一特定证据，而不仅仅是基于全省考生的总体情况来判断

后验概率的本质是在先验概率的基础上，结合观测到的证据（如小李的学习排名、模拟成绩等具体数据）对假设可能性的更新。那么，这些证据如何影响概率计算呢？关键在于一个核心概念 ——似然：它描述的是‘在给定假设的情况下，观测到特定证据的概率’

似然

以小李高考为例，先回顾基础概率：

先验概率：河南考生考上一本的总体概率P(一本) = 10%，不考虑个体特征。

后验概率：已知小李成绩前 5% 且模拟达线，考上一本的概率P（一本|优秀成绩）= 80%，是结合证据后的更新概率。

似然描述的是 “在给定某一假设（或类别）的情况下，观察到特定证据的概率”，记作P(证据|假设。它与后验概率的区别在于条件和结果的倒置：

后验概率：已知证据，假设成立的概率”（如已知小李成绩优秀，他考上一本的概率）。

似然：即 “若假设成立，观察到该证据的概率”（如假设小李能考上一本，他成绩优秀的概率）。

似然是连接 “假设” 与 “证据” 的桥梁，它不直接回答 “假设是否成立”，而是回答 “假设成立时，证据出现的可能性有多大”，为后验概率的推导提供关键的证据权重。

花了大篇幅解释了先验后验和似然那我们回到本身 贝叶斯决策论 是干嘛用的

贝叶斯决策论核心在于利用已知的概率信息（先验概率、后验概率等）以及误判损失，来选择最优的决策方案，也就是最优的类别标记。

类别标记

假设有N种可能的类别标记，用集合y={c1,c2,⋯,cN}表示。比如在图像分类中，N可以是不同物体类别数量，以高考举例c1可能代表 “一本录取”， c2代表 “二本录取” 等。

误判损失λij

λij表示将真实标记为ci的样本误分类为cj所产生的损失。

后验概率P(ci∣x)

P(ci∣x)是在给定样本特征x的情况下，样本属于类别ci的概率。

期望损失（条件风险）

公式如下：

举个栗子：

所以说我们的任务是

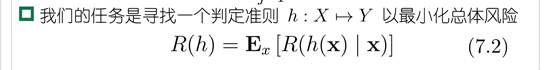
说人话：对每个样本的条件风险进行加权平均

中译中：

还是以高考为例子：

贝叶斯最优分类器

小张平时成绩优异，高考发挥稳定，模拟考试成绩也远超一本线，且相关竞赛获奖等情况也突出，那么将他判定为 “一本录取” 时的条件风险可能最小。因为若误判他为其他更低的录取类别，会造成人才培养资源的不合理分配，且对他个人发展不利，损失较大；而正确判定为一本，损失几乎为 0 。通过比较不同录取类别判定下的条件风险，最终确定的这个最优判定规则h*，就是贝叶斯最优分类器。

贝叶斯风险R(h*)：

当使用贝叶斯最优分类器h*对所有考生进行录取类别判定时，此时的总体风险R(h*)就是贝叶斯风险。它代表了在这种最优的录取决策方式下，整个考生群体面临的平均期望损失。

1- R(h*)

方式精度的理论上限

PPT上给的例子

当i = j时，即预测的录取结果和真实的录取结果一致，比如预测某考生是一本录取，实际该考生也被一本录取，此时误判损失= 0，因为没有产生错误分类的不良后果。反之为1

将损失带入条件风险中：

化简的到

为了使条件风险最小那么需要P（C|X）最大所以的出

所以我们的任务转变为找到后验概率最大的类

对于生成式模型

极大似然估计

概率模型的训练过程就是参数估计过程，统计学界的两个学派提供了不同的方案:

频率主义学派(frequentist)

认为参数虽然未知，但却存在客观值，因此可通过优化似然函数等准则来确定参数值

贝叶斯学派（Bayesian)

认为参数是未观察到的随机变量、其本身也可由分布，因此可假定参数服从一个先验分布，然后基于观测到的数据计算会数的后—分布

以你会不会给我这篇文章点赞为例

频率主义学派会认为 “你会不会给这篇文章点赞” 存在一个客观概率值。为确定这个值，频率主义者会收集大量与你类似的用户在面对相似文章时的点赞情况。频率主义学派认为这个值就是你给文章点赞概率的客观体现，不依赖于任何主观判断，重点在于通过大量数据的统计来逼近这个客观存在的概率参数。

贝叶斯学派把 “你会不会给这篇文章点赞” 的概率看成一个随机变量。在没有任何关于你和这篇文章的具体信息之前，先假定一个关于你点赞概率的先验分布。然后，基于观测到的数据来更新这个分布。比如了解到你过往对相关主题文章的点赞频率、这篇文章的标题关键词对你的吸引力、文章的篇幅等信息后，利用贝叶斯公式结合先验分布，计算出后验分布。后验分布综合了先验信息和新观测到的数据信息，更准确地反映了你给这篇文章点赞的概率。

（点个赞吧点个赞吧点个赞吧点个赞吧点个赞吧点个赞吧点个赞吧点个赞吧）