💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
文献来源:

本文针对机械故障的特征提取量身定制了一种新的分解理论——特征模态分解(FMD)。所提出的FMD本质上是通过设计的自适应有限脉冲响应(FIR)滤波器分解不同的模式。FMD利用相关峰度的优越性,同时考虑了故障信号的冲动性和周期性。首先,通过汉宁窗口初始化设计的FIR滤波器组为分解提供方向;然后使用周期估计和更新过程来锁定故障信息。最后,在模式选择过程中去除冗余和混合模式。使用从轴承单个和复合故障收集的模拟和实验数据,证明了FMD的优越性,可以自适应和准确地分解故障模式,并对其他干扰和噪声具有鲁棒性。此外,已经证明FMD在机械故障特征提取方面优于最流行的变分模态分解。
📚2 运行结果


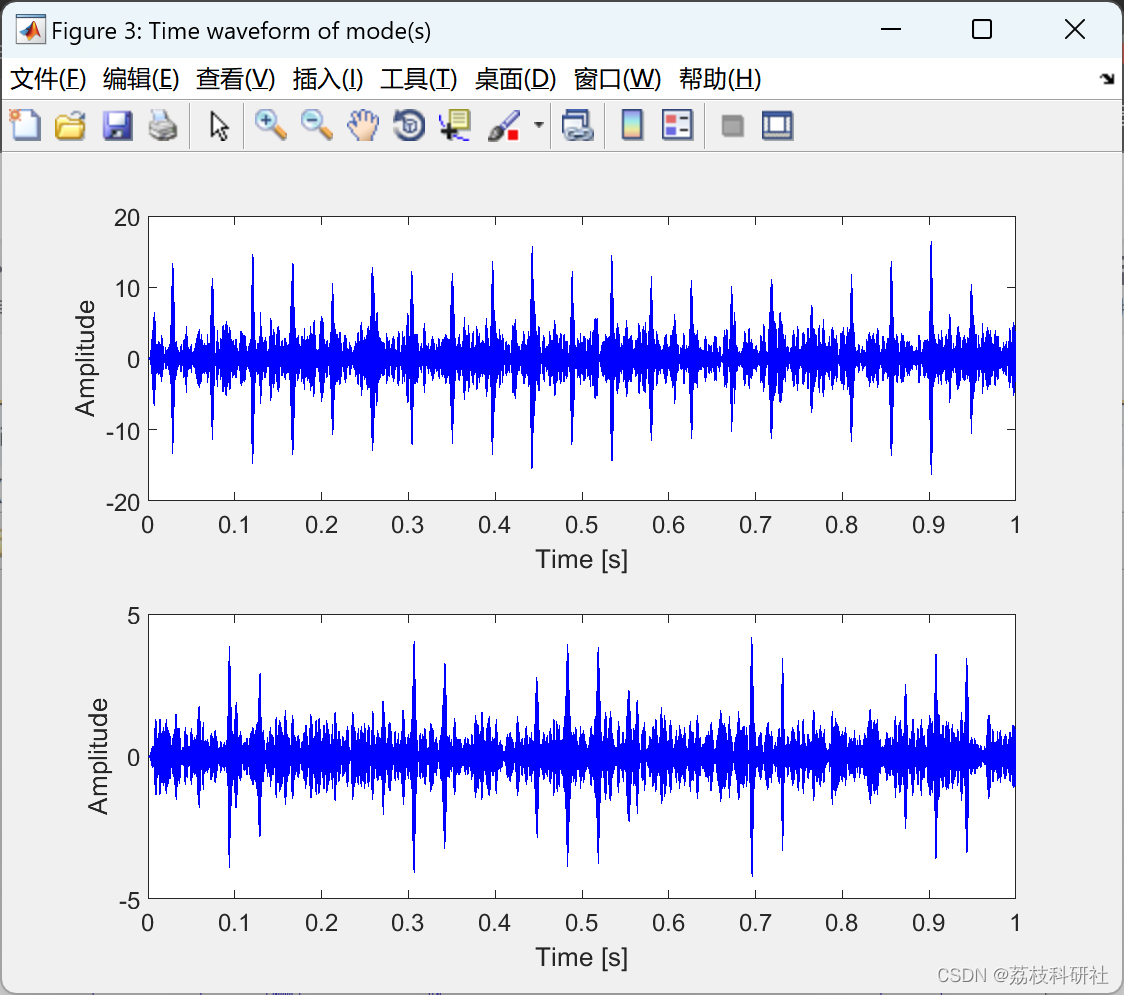


部分代码:
% FMD
tic
y_final = FMD(fs, x, filtersize, cutnum, modenum, maxiternum);
toc
% Plot
b = size(y_final, 2);
figure('Name', 'Time waveform of mode(s)')
for k = 1:b
subplot(b, 1, k)
plot(t, y_final(:, k), 'b')
xlabel('Time [s]');
ylabel('Amplitude');
end
figure('Name', 'FFT amplitude spectrum of mode(s)')
for k = 1:b
subplot(b, 1, k)
[ff, amp] = myfft(fs, y_final(:, k), 0);
plot(ff, amp / max(amp), 'r');
xlabel('Frequency [Hz]');
ylabel('Amplitude');
end
figure('Name', 'Hilbert envelope spectrum of mode(s)')
for k = 1:b
subplot(b, 1, k)
envelope = abs(hilbert(y_final(:, k))) - mean(abs(hilbert(y_final(:, k))));
[ff, amp] = myfft(fs, envelope, 1);
xlabel('Frequency [Hz]');
ylabel('Amplitude');
xlim([0 300])
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Yonghao, Miao, et al. “Feature Mode Decomposition: New Decomposition Theory for Rotating Machinery Fault Diagnosis.” IEEE Transactions on Industrial Electronics, Institute of Electrical and Electronics Engineers (IEEE), 2022, pp. 1–1, doi:10.1109/tie.2022.3156156.





















 4004
4004

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








