利用librosa,torchaudio分别实现梅尔语谱图（Mel spectrogram ）音频特征提取的详细过程

  本文主要是实现音频到梅尔谱的转变，说简单也简单，因为可以利用PyTorch库里面的torchaudio直接调用相应的库或则直接调用librosa库即可实现，说难也难，因为不采用直接调用的话，拆分到每一步来实现就比较困难了。

语言：python

工具包:librosa,torchaudio

实现方式：直接调用、分步实现

摘要：用不同的方式实现音频到梅尔谱的转变，如torchaudio，librosa，直接调用和分步实现，把音频的特征值提取出来，可用于音频分类

关键词：短时傅里叶变换（STFT）、语谱图、快速傅里叶变换（FFT），分帧、加窗、频谱图、功率谱、离散傅里叶变换（DFT）、离散余弦傅里叶变换（DCT）、梅尔谱

一、直接调用（torchaudio库）

        1.加载音频

import torchaudio
waveform,sample_rate = torchaudio.load(filename)
#filename:音频文件地址，格式为wav
#waneform:波形
#sample_rate:采样率

说明：

torchaudio.load（）的返回值：波形 ( Tensor，float32，范围：[-1,1]) 和采样率 ( int) 的元组。

举例:

import torchaudio
import matplotlib.pyplot as plt

#加载wav音频文件输出图像
filename = "/home/yc/vs_code/pytorch_audio/ESC-50/ESC-50-master/audio/1-137-A-32.wav"
waveform,sample_rate = torchaudio.load(filename)
print("音频大小:{}".format(waveform.shape)) #输出音频大小
print("采样率:{}".format(sample_rate))#输出采样率
print(type(waveform))#输出波形类型
#画图
plt.figure()
plt.plot(waveform.t().numpy())
plt.show()

输出：

音频大小:torch.Size([1, 220500])
采样率:44100
<class 'torch.Tensor'>

图1

说明：该wav文件是ESC-50数据集中的某个音频，时长5秒，torchaudio默认采样率是44100hz,故共有220500个采样点，1表示单通道。返回的是tensor类型（张量）

        2.输出梅尔谱

torchaudio.transforms.MelSpectrogram(sample_rate: int = 16000, n_fft: int = 400, 
                                     win_length[int]:None, hop_length[int] = None, 
                                     f_min: float = 0.0, f_max[float] = None,
                                     pad: int = 0, n_mels: int = 128, 
                                     window_fn:(...) -> Tensor=torch.hann_window ,
                                     power: float = 2, normalized: bool = False, 
                                     wkwargs[dict] = None, center: bool = True, 
                                     pad_mode: str = 'reflect', onesided: bool = None, 
                                     norm[str] = None, mel_scale: str = 'htk')

参数说明：

sample_rate(int) ：输入波形的采样率
n_fft(int) ：为FFT的长度，默认为400，会生成 n_fft /2 + 1 个 bins
win_length ：窗口的长度，默认为 n_fft
hop_length ：相邻两个滑动窗口帧之间的距离，即帧移，默认为 win_length / 2
f_min(float) ：音频的最小频率，默认为0.0（可以设为20,为了滤去噪声，在频域中表为左下角为一条线）
f_max(float) ：音频的最大频率，默认为None
pad ：对输入信号两边的补零长度，默认为 0
n_mels(int) ：mel滤波器的个数，默认为128
window_fn ：窗函数，默认为 torch.hann_window
power(float) ：语谱图的幂指数，值必须大于 0，默认为 2.0（代表功率），取 1（ 代表能量）
normalized(bool) ：对stft的输出进行归一化，默认为 False
wkwargs ：窗函数的参数，默认为 None（附加参数，为字典类型，暂时不用。如果需要传参数，就要调用这个参数）
center(bool) ：是否对输入tensor在两端进行padding，默认为 True
pad_mode(str) ：补零方式，默认为 reflect
onesided(bool) ：是否只计算一侧的谱图，默认为 True，即返回单侧的语谱图，如果为 False，则返回全部的谱图。
norm(str)：默认为None， 为“slaney”时，则将三角形mel权重除以mel bin的宽度（即进行面积归一化），
mel_scale(str) ：采用的mel尺度: htk 或者 slaney，默认 htk

举例

import torchaudio
import matplotlib.pyplot as plt

#加载wav音频文件输出图像
filename = "/home/yc/vs_code/pytorch_audio/ESC-50/ESC-50-master/audio/1-137-A-32.wav"
waveform,sample_rate = torchaudio.load(filename)

#梅尔谱
specgram = torchaudio.transforms.MelSpectrogram()(waveform)
print("梅尔谱大小:{}".format(specgram.shape))
plt.figure()
p = plt.imshow(specgram.log2()[0,:,:].detach().numpy(),cmap='gray')
plt.show()

输出

梅尔谱大小:torch.Size([1, 128, 1103])

图2

说明：

torch.Size([1, 128, 1103])当中，1表示单通道；128表示梅尔滤波器的个数；1103表示时间（也就是帧数）

这里补充以下计算帧数的公式：nf=(N− overlap) / inc =(N−wlen)/inc+1；其中，wlen为帧长，inc为帧移，重叠部分为overlap，overlap=wlen - inc，N为采样率，nf为帧数

二、直接调用（librosa库）

        1.加载音频

import librosa
import matplotlib.pyplot as plt

filename="/home/yc/vs_code/上传源码/1-137-A-32.wav"
waveform,sr=librosa.load(filename)
print("音频序列：{}".format(waveform))
print("音频总样本数量:{}".format(waveform.size)) #输出音频大小
print("采样率:{}".format(sr))#输出采样率
print("音频类型：{}".format(type(waveform)))
print("音频形状：{}".format(waveform.shape))

#画图
plt.figure()
librosa.display.waveshow(waveform)
plt.show()

输出：

音频序列：[0.00658327 0.0095392  0.00643882 ... 0.00137593 0.00287526 0.00399888]
音频总样本数量:110250
采样率:22050
音频类型：<class 'numpy.ndarray'>
音频形状：(110250,)

说明：

该wav文件是ESC-50数据集中的某个音频，时长5秒，librosa默认采样率22050hz,故共有110250个采样点，返回的是numpy数组。

                                                                                图3

2.输出梅尔谱

spectrogram=librosa.feature.melspectrogram(y,sr,
                                           S=None,n_fft=2048,
                                           hop_length=512,win_length=2048,
                                           window="hann",center=True,
                                           pad_mode="constant",power=2,
                                           n_mels=40,fmin=0,fmax=sr/2,
                                           htk=0,norm=None
                                           )

说明：

参数：

        y：音频时间序列,numpy数组。支持多通道
        sr ：采样率，默认22050
        S ：语频谱，默认None
        n_fft ：FFT窗口的长度，默认2048
        hop_length ：帧移，默认512，n_fft/4
        win_length ：窗口的长度为win_length，默认win_length = n_fft
        window ：窗函数，默认hann
        center：bool
        如果为True，则填充信号y，以使帧 t以y [t * hop_length]为中心。
        如果为False，则帧t从y [t * hop_length]开始

        pad_mode:补零模式，默认constant
        power：幅度谱的指数。例如1代表能量，2代表功率，等等
        n_mels：滤波器组的个数 ，默认40

        f_min(float) ：音频的最小频率，默认为0.0（可以设为20,为了滤去噪声，在频域中表为左下角为一条线）
        f_max(float) ：音频的最大频率，默认为sr/2

        norm(str)：默认为None，｛None、slaney或number｝[标量],如果是“slaney”，则将三角形的mel权重除以的宽度,mel波段（区域归一化）。如果是数字，请使用“librosa.util.normalize”对每个筛选器进行标准化，按单位lp范数。请参阅“librosa.util.normalize”以获取完整的支持的范数值的描述（包括“+-np.inf”）。

        mel_scale(str) ：采用的mel尺度: htk 或者 slaney，默认 htk

返回：

    Mel频谱shape=(n_mels, t)（梅尔滤波器个数，时间）

代码实现：

import librosa
import matplotlib.pyplot as plt
import numpy as np


audio_data = '/home/yc/vs_code/pytorch_audio/ESC-50/ESC-50-master/audio/1-137-A-32.wav'
x , sr = librosa.load(audio_data)

mel_spect = librosa.feature.melspectrogram(y=x, sr=sr)
mel_spect = librosa.power_to_db(mel_spect, ref=np.max)
librosa.display.specshow(mel_spect, y_axis='mel', fmax=sr/2, x_axis='time')
plt.title('Mel Spectrogram')
plt.colorbar(format='%+2.0f dB')
plt.show()

输出：

                                                                        图4

三、分步实现(librosa)

                                                                        图5

 

图5中，分帧+加窗+FFT=短时傅里叶变换（STFT）

1.语谱图 spectrogram

（1）定义

在音频、语音信号处理领域，我们需要将信号转换成对应的语谱图(spectrogram)，将语谱图上的数据作为信号的特征。语谱图的横坐标是时间，纵坐标是频率，坐标点值为语音数据能量。由于是采用二维平面表达三维信息，所以能量值的大小是通过颜色来表示的，颜色深，表示该点的语音能量越强。如图4所示

                                                                        图6

（2）实现步骤

1. 对信号进行预加重
2. 再进行分帧加窗，进行STFT， 得到每帧信号的频谱图；
3. 对频谱图进行旋转 加映射；
4. 将变换后的多帧频谱进行拼接， 形成语谱图；

        1.1预加重

通常来讲语音或音频信号的高频分量强度较小，低频分量强度较大，信号预加重就是让信号通过一个高通滤波器，让信号的高低频分量的强度不至于相差太多。在时域中，对信号x[n]作如下操作：
 

α通常取一个很接近1的值，为0.97或0.95.
从时域公式来看，可能有部分人不懂为啥这是一个高通滤波器，我们从z变换的角度看一下滤波器

可以看出滤波器有一个极点0，和一个零点α。
当频率为0时，z=1, 放大系数为(1-α）。当频率渐渐增大，放大系数不断变大，当频率到pi时，放大系数为(1+α)（可由几何画法得出）

离散域中，[0,π] 对应连续域中的 [0,fs/2] (单位Hz)。其中fs为采样率
因此当频率到22000Hz时，放大系数为 (1+α)。

下面用两段代码和对应的图像给出一个直观感受:

alpha = 0.97#预加重的系数
tmin=0
tmax=5
emphasized_y = np.append(waveform[tmin*sr],
                         waveform[tmin*sr+1:tmax*sr]-alpha*waveform[tmin*sr:tmax*sr-1])
n = int((tmax-tmin)*sr) #信号一共的sample数量

#未经过预加重的信号频谱（图5）
plt.figure()
freq = sr/n*np.linspace(0,n/2,int(n/2)+1)
plt.plot(freq,np.absolute(np.fft.rfft(waveform[tmin*sr:tmax*sr],n)**2)/n)
plt.xlim(0,5000)
plt.xlabel('Frequency/Hz',fontsize=14)
plt.show()

#预加重之后的信号频谱（图6）
plt.figure()
plt.plot(freq,np.absolute(np.fft.rfft(emphasized_y,n)**2)/n)
plt.xlim(0,5000)
plt.xlabel('Frequency/Hz',fontsize=14)
plt.show()

                                                                        图7

                                                                        图8

注：1. librosa.load得到的音频序列是numpy序列；torchaudio.load() 得到的音频序列是tensor类型

        2. 这两段代码里用了函数librosa.fft.rfft(y,n)，rfft表示经过fft变换之后只取其中一半（因为另一半对应负频率，没有用处）, y对应信号，n对应要做多少点的FFT。我们这里的信号有44.1k*5=220500 个点，所以对应的FFT 也做220500点的FFT，每一个点所对应的实际频率是该点的索引值*fs/n，这是咋得出来的？因为第220500个点应该对应(约等于)fs(或者离散域中的 2 π )，所以前面的点根据线性关系一一对应即可。这里只展示0-8000Hz，可以看出，经过预加重之后的信号高频分量明显和低频分量的差距没那么大了。

这样预加重的好处有什么?
(1)就是我们刚刚提到的平衡一下高频和低频
(2)避免FFT中的数值问题(也就是高频值太小出现在分母的时候可能会出问题)
(3)或许可以提高SNR（信噪比）

3. python使用matplotlib绘图总结

1.2分帧

预处理完信号之后，要把原信号按时间分成若干个小块，一块就叫一帧(frame)。

为啥要做这一步？因为原信号覆盖的时间太长，用它整个来做FFT，我们只能得到信号频率和强度的关系，而失去了时间信息。

我们想要得到频率随时间变化的关系，所以完成以下步骤

    将原信号分成若干帧，
    对每一帧作FFT（又称为短时FFT，因为我们只取了一小段时间)，然后对每一帧频谱进行映射。
    最后将得到的结果按照时间顺序拼接起来。

这就是语谱图(spectrogram)的原理。

代码和图像如下图所示：
 

举例

#分帧
alpha = 0.97#预加重的系数
tmin=0
tmax=5
emphasized_y = np.append(waveform[tmin*sr],
                         waveform[tmin*sr+1:tmax*sr]-alpha*waveform[tmin*sr:tmax*sr-1])

frame_size, frame_stride = 0.025,0.01#frame_size：每一帧的长度。frame_stride：相邻两帧的间隔
frame_length, frame_step = int(round(sr*frame_size)),int(round(sr*frame_stride))
signal_length = (tmax-tmin)*sr
frame_num = int(np.ceil((signal_length-frame_length)/frame_step))+1 #向上舍入
pad_frame = (frame_num-1)*frame_step+frame_length-signal_length #不足的部分补零
pad_y = np.append(emphasized_y,np.zeros(pad_frame))
signal_len = signal_length+pad_frame

print("frame_length:",frame_length)# 每一帧对应的sample数量
print("frame_step:",frame_step)#相邻两帧的sample数量
print("signal_length:",signal_length)#音频的总sample数量
print("frame_num:",frame_num)#整个信号所需要的帧数
print("pad_frame:",pad_frame)#需要补零的sample数量
print("pad_y:",pad_y)#预加重、补零之后的音频列表
print("signal_len:",signal_len)#预加重、分帧之后的音频总sample数量

                                                                        输出

说明：1. round函数的使用

2.在进行语谱图之前， 先对信号定义下面几个变量:

    frame_size: 每一帧的长度。通常取20-40ms。太长会使时间上的分辨率(time resolution)较小，太小会加重运算成本。 这里取25ms.

    frame_length: 每一帧对应的sample数量。
    等于fs*frame_size。我们这里是22050*0.025=551.

    frame_stride: 相邻两帧的间隔。通常间隔必须小于每一帧的长度，即两帧之间要有重叠，否则我们可能会失去两帧边界附近的信息。
    做特征提取的时候，我们是绝不希望丢失有用信息的。 这里取10ms，即有60%的重叠。

    frame_step: 相邻两帧的sample数量。这里是220.

    frame_num: 整个信号所需要的帧数。
    一般希望所需要的帧数是个整数值，所以这里要对信号补0 (zero padding)让信号的长度正好能分成整数帧。

1.3加窗

分帧完毕之后，对每一帧加一个窗函数，以获得较好的旁瓣下降幅度。通常使用hamming window。

为啥要加窗？

要注意，即使我们什么都不加，在分帧的这个过程中也相当于给信号加了矩形窗，离散滤波器设计的内容中指出：

矩形窗的频谱有很大的旁瓣，时域中将窗函数和原函数相乘，相当于频域的卷积，矩形窗函数和原函数卷积之后，由于旁瓣很大，会造成原信号和加窗之后的对应部分的频谱相差很大，这就是频谱泄露 。hamming window有较小的旁瓣，造成的spectral leakage也就较小。

代码实现如下：

#加窗
indices = np.tile(np.arange(0, frame_length), (frame_num, 1)) + np.tile(
    np.arange(0, frame_num * frame_step, frame_step), (frame_length, 1)).T
frames = pad_y[indices] #frame的每一行代表每一帧的sample值
frames *= np.hamming(frame_length) #加hamming window 注意这里不是矩阵乘法
print(frames)#加窗完之后的数据

输出：

[[ 5.26661947e-04  2.52368184e-04 -2.25473560e-04 ...  3.76132508e-06
   1.37387336e-05  1.12662837e-05]
 [-1.76738948e-05 -2.18316429e-04 -1.73130231e-05 ...  3.28833144e-05
   2.13895869e-05  1.88434497e-05]
 [ 1.10267475e-05 -9.14076453e-06 -1.04634426e-05 ...  9.04791189e-06
   1.50709128e-05  7.06589781e-06]
 ...
 [ 7.67913461e-05  4.84513458e-04  6.50985474e-04 ... -7.54293720e-04
  -4.56368876e-04 -1.95991993e-04]
 [ 3.69879007e-04 -7.32277266e-03 -4.64798599e-03 ... -3.55405822e-04
  -2.05636392e-04 -6.61829580e-05]
 [-5.73425144e-04  5.61288561e-04  1.19895244e-03 ...  0.00000000e+00
   0.00000000e+00  0.00000000e+00]]

说明;

1.     首先定义indices变量，这个变量生成每帧所对应的sample的索引。
2.     np.tile()函数可以使得array从行或者列扩展。
3.     然后定义frames，对应信号在每一帧的值。frames共有500行，551列，分别对应一共有500帧和每一帧有551个sample。
4. 将得到的frames和hamming window直接相乘即可，注意这里不是矩阵乘法。
    

1.4  FFT--->功率谱（使用dB单位）-->语谱图（此处等价为功率谱）
1.4.1 FFT--->功率谱

1. 多帧信号做FFT， 在上一节中获得了frames变量，其每一行对应每一帧，所以我们分别对每一行做FFT。（ 这里需要注意， 不同的分帧算法实现，定义不一样， 有的是将每一列作为一帧， 自己看代码时， 需要进行区分）
2. 由于每一行是551个点的信号，所以可以选择512点FFT（FFT点数比原信号点数少会降低频率分辨率frequency resolution，但这里相差很小，所以可以忽略）。
3. 将得到的FFT变换取其magnitude，并进行平方再除以对应的FFT点数，即可得到功率谱（取频谱模平方， 求功率谱power spectrum ）。
4.     功率谱，代表的是信号本身在不同的频率成分上各自所包含的功率（或者能量），通过检查一个信号的功率谱，可以确定信号中存在哪些频率以及它们的相对强度。 其横坐标代表是频率，通常使用Hz 单位，频率轴可以对数的，这样任意两个频率成分之间是对数关系。纵坐标，代表了每个频率成分所对应的能量， 通常使用dB 单位。功率谱图中的高度代表了，在某一个频段区间内， 该频段内的能量（或者说功率）。

1.4.2功率谱（使用dB单位）-->语谱图

原始信号所对应的，无论频谱还是功率谱，反应的都是信号在各个频率分量上的信息。 但是，这两者都丢失了信号在时间维度上的信息。从而，为了将一个信号同时表达出，信号在频率分量上的信息，又要显示出信号随着时间变化的信息。 这便是语谱图的本意。语谱图的横坐标表示时间， 纵坐标是频率，每个点上数值强度或者颜色深度表示该点在时频上的特性。

    注意： 如何从功率谱得到语谱图呢？
    使用短时傅里叶变换。

1.         即在对信号进行分帧之后;
2.         对每一帧信号计算其对应的功率谱。
3.         再将该功率谱垂直翻转90度， 从而便得到当前帧的语谱图形式，此时纵轴便是频率，横轴是当前帧时间上的信息；
4.         重复第2, 3 步骤，便会将多个帧的功率谱在时间维度上，按照时间的先后顺序拼接起来，从而构成了语谱图。

    所以，语谱图便是将每一帧信号的功率谱做成一个合集（每一帧信号都有一个功率谱)。将多个帧的功率谱，翻转之后，按照时间顺序拼接，就构成信号的spectrogram)。此时, 使用每一帧信号的功率谱， 构成一个功率谱的合集， 该功率谱合集便是等价于语谱图。

代码实现：

#FFT--->功率谱（使用dB单位）-->语谱图（此处等价为功率谱）
NFFT = 512 #frame_length=551
mag_frames = np.absolute(np.fft.rfft(frames,NFFT))#由于rfft之后，返回的是复数，故要对其取进行模操作
pow_frames = mag_frames**2/NFFT#Pow_frames就是功率谱矩阵的变量名.

print(pow_frames.shape)

plt.figure()
plt.imshow(20*np.log10(pow_frames[40:].T),cmap=plt.cm.jet,aspect='auto')
plt.yticks([0,128,256],np.array([0,128,256])*sr/NFFT)
plt.show()

                                                                        图9

1.5语谱图(spectrogram)-->梅尔谱(mel-spectrogram)

• mel-spectrogram就是将梅尔滤波器组应用到语谱图中。此时，语谱图的纵坐标从Hz 刻度便转换成Mel刻度；Mel尺度和普通频率之间使用如下转换公式：

• Mel(f) = 2595 * log10(1 + f/700)
  

• 注意，在实际的代码中，会有另外的公式，即在1000Hz, 内使用线性变换，　超过1000Hz 后再使用如上的变换。

1.5.1Mel 滤波器组

所谓梅尔滤波器组是一个等高的三角滤波器组，每个滤波器的起始点在上一个滤波器的中点处。其对应的频率在梅尔尺度上是线性的，因此称之为梅尔滤波器组。

    每个滤波器对应的频率可以将最大频率（下图中是4000，我们这里是22.05k)用上文中提到的公式转换成梅尔频率，在梅尔尺度上线性分成若干个频段，再转换回实际频率尺度即可。

实际操作时，将每个滤波器分别和功率谱pow_frames进行点乘，获得的结果即为该频带上的能量(energy)。

这里我们的pow_frames是一个(500,513)的矩阵(500：音频的总帧数；513：n_fft/2+1）

1.5.2 Mel 滤波器的个数与n_fft 点数之间的关系

• 梅尔滤波器fbank是一个(mel_N, 513)的矩阵，其中mel_N代表对应的梅尔滤波器个数，这个值不能太大，因为这里我们一共只有513个点，如果mel_N取得太大，会导致前面几个滤波器的长度都是0 (因为低频的梅尔滤波器特别窄)。
• 梅尔滤波器的数量越多，低频滤波器分到的频率点数越少，相应的就需要 N F F T N_{FFT} NFFT​ 提高，否则低频滤波器对应的点数太少甚至为0.
• 我们只要将这两个矩阵相乘pow_frames*fbank.T即可得到mel-spectrogram，结果是一个(500, 40)的矩阵，每一行是一帧，每一列代表对应的梅尔频带的能量。

如下图：

                                                                             图10

1.5.3 Mel 滤波器计算公式

具体梅尔滤波器的图例和计算公式以及对应代码如下:

其中m代表滤波器的序号，f(m-1)和f(m)、f(m+1)分别对应第m个滤波器的起始点、中间点和结束点。f(m)对应的值不是频率值，而是对应的sample的索引！比如，我们这里最大频率是2756(22050*5/40) Hz, 所以2756对应的是第513个sample，即频率f所对应的值是f/fs*NFFT。

1.5.4代码实现

#语谱图(spectrogram)-->梅尔谱(mel-spectrogram)
#下面定义mel filter
mel_N = 40 #滤波器数量,这个数字若要提高，则NFFT也要相应提高
mel_low, mel_high = 0, (2595*np.log10(1+(sr/2)/700))
mel_freq = np.linspace(mel_low,mel_high,mel_N+2)
hz_freq = (700 * (10**(mel_freq / 2595) - 1))
bins = np.floor((NFFT)*hz_freq/sr) #将频率转换成对应的sample位置
fbank = np.zeros((mel_N,int(NFFT/2+1))) #每一行储存一个梅尔滤波器的数据
for m in range(1, mel_N + 1):
    f_m_minus = int(bins[m - 1])   # left
    f_m = int(bins[m])             # center
    f_m_plus = int(bins[m + 1])    # right
 
    for k in range(f_m_minus, f_m):
        fbank[m - 1, k] = (k - bins[m - 1]) / (bins[m] - bins[m - 1])
    for k in range(f_m, f_m_plus):
        fbank[m - 1, k] = (bins[m + 1] - k) / (bins[m + 1] - bins[m])
filter_banks = np.matmul(pow_frames, fbank.T)#将梅尔滤波器作用到上一步得到的pow_frames上
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)  # np.finfo(float)是最小正值
filter_banks = 20 * np.log10(filter_banks)  # dB
#filter_banks -= np.mean(filter_banks,axis=1).reshape(-1,1)
# plt.figure(dpi=300,figsize=(12,6))
plt.figure()
plt.imshow(filter_banks[40:].T, cmap=plt.cm.jet,aspect='auto')
plt.yticks([0,10,20,30,39],[0,1200,3800,9900,22000])
plt.show()

输出：

                                                                                图11

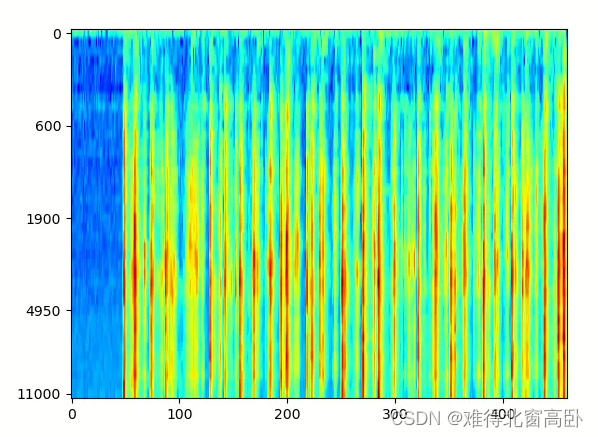
说明:

• 代码中有一段np.where(condition,a,b)，这个函数的功能是检索b中的元素，当condition满足的时候，输出a。否则，输出b中的原元素。这一步的操作是为了将其中的全部0值以一个很小的非负值代替，否则在计算dB的时候，log中出现0会出错。
• 机器学习的时候，每一个音频段即可用对应的mel-spectogram表示，每一帧对应的某个频段即为一个feature。因此我们一共获得了500*40个feature和对应的值。实际操作中，每个音频要采用同样的长度，这样我们的feature数量才是相同的。通常还要进行归一化，即每一帧的每个元素要减去该帧的平均值，以保证每一帧的均值均为0。
• np.linspace（）说明
• np.matmul ()

完整代码：

import librosa
import numpy as np
import matplotlib.pyplot as plt

#加载wav音频文件输出图像
filename = "/home/yc/vs_code/pytorch_audio/ESC-50/ESC-50-master/audio/1-137-A-32.wav"
waveform , sr = librosa.load(filename)

print("音频大小:{}".format(waveform.size)) #输出音频大小
print("采样率:{}".format(sr))#输出采样率

alpha = 0.97
tmin=0
tmax=5
emphasized_y = np.append(waveform[tmin*sr],
                         waveform[tmin*sr+1:tmax*sr]-alpha*waveform[tmin*sr:tmax*sr-1])
n = int((tmax-tmin)*sr) #信号一共的sample数量

#未经过预加重的信号频谱
plt.figure()
freq = sr/n*np.linspace(0,n/2,int(n/2)+1)
plt.plot(freq,np.absolute(np.fft.rfft(waveform[tmin*sr:tmax*sr],n)**2)/n)
plt.xlim(0,8000)
plt.xlabel('Frequency/Hz',fontsize=14)
plt.show()

#预加重之后的信号频谱
plt.figure()
plt.plot(freq,np.absolute(np.fft.rfft(emphasized_y,n)**2)/n)
plt.xlim(0,8000)
plt.xlabel('Frequency/Hz',fontsize=14)
plt.show()

frame_size, frame_stride = 0.025,0.01#frame_size：每一帧的长度。frame_stride：相邻两帧的间隔
frame_length, frame_step = int(round(sr*frame_size)),int(round(sr*frame_stride))
signal_length = (tmax-tmin)*sr
frame_num = int(np.ceil((signal_length-frame_length)/frame_step))+1 #向上舍入
pad_frame = (frame_num-1)*frame_step+frame_length-signal_length #不足的部分补零
pad_y = np.append(emphasized_y,np.zeros(pad_frame))
signal_len = signal_length+pad_frame

print("frame_length:",frame_length)# 每一帧对应的sample数量
print("frame_step:",frame_step)#相邻两帧的sample数量
print("signal_length:",signal_length)#音频的总sample数量
print("frame_num:",frame_num)#整个信号所需要的帧数
print("pad_frame:",pad_frame)#需要补零的sample数量
print("pad_y:",pad_y)#预加重、补零之后的音频列表
print("signal_len:",signal_len)#预加重、分帧之后的音频总sample数量

#加窗
indices = np.tile(np.arange(0, frame_length), (frame_num, 1)) + np.tile(
    np.arange(0, frame_num * frame_step, frame_step), (frame_length, 1)).T
frames = pad_y[indices] #frame的每一行代表每一帧的sample值
frames *= np.hamming(frame_length) #加hamming window 注意这里不是矩阵乘法
print(frames)

#FFT--->功率谱（使用dB单位）-->语谱图（此处等价为功率谱）
NFFT = 512 #frame_length=551
mag_frames = np.absolute(np.fft.rfft(frames,NFFT))#由于rfft之后，返回的是复数，故要对其取进行模操作
pow_frames = mag_frames**2/NFFT#Pow_frames就是功率谱矩阵的变量名.

print(pow_frames.shape)

plt.figure()
plt.imshow(20*np.log10(pow_frames[40:].T),cmap=plt.cm.jet,aspect='auto')
plt.yticks([0,64,128,192,256],np.array([0,64,128,192,256])*sr/NFFT)

plt.show()

#语谱图(spectrogram)-->梅尔谱(mel-spectrogram)
#下面定义mel filter
mel_N = 40 #滤波器数量,这个数字若要提高，则NFFT也要相应提高
mel_low, mel_high = 0, (2595*np.log10(1+(sr/2)/700))
mel_freq = np.linspace(mel_low,mel_high,mel_N+2)
hz_freq = (700 * (10**(mel_freq / 2595) - 1))
bins = np.floor((NFFT)*hz_freq/sr) #将频率转换成对应的sample位置
fbank = np.zeros((mel_N,int(NFFT/2+1))) #每一行储存一个梅尔滤波器的数据
for m in range(1, mel_N + 1):
    f_m_minus = int(bins[m - 1])   # left
    f_m = int(bins[m])             # center
    f_m_plus = int(bins[m + 1])    # right
 
    for k in range(f_m_minus, f_m):
        fbank[m - 1, k] = (k - bins[m - 1]) / (bins[m] - bins[m - 1])
    for k in range(f_m, f_m_plus):
        fbank[m - 1, k] = (bins[m + 1] - k) / (bins[m + 1] - bins[m])
filter_banks = np.matmul(pow_frames, fbank.T)#将梅尔滤波器作用到上一步得到的pow_frames上
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)  # np.finfo(float)是最小正值
filter_banks = 20 * np.log10(filter_banks)  # dB
plt.figure()
plt.imshow(filter_banks[40:].T, cmap=plt.cm.jet,aspect='auto')
plt.yticks([0,10,20,30,39],[0,600,1900,4950,11000])
plt.show()

参考连接：
语谱图（一） Spectrogram 的定义与机理-CSDN博客

语谱图（四） Mel spectrogram 梅尔语谱图_melspectrogram-CSDN博客