一、一元线性回归
1.概念
线性回归模型是利用线性拟合的方式探寻数据背后的规律。如下图,先通过搭建线性回归模型寻找这些散点(也称样本点)背后的趋 势线(也称回归曲线),再利用回归曲线进行一些简单的预测分析或因果关系分析。
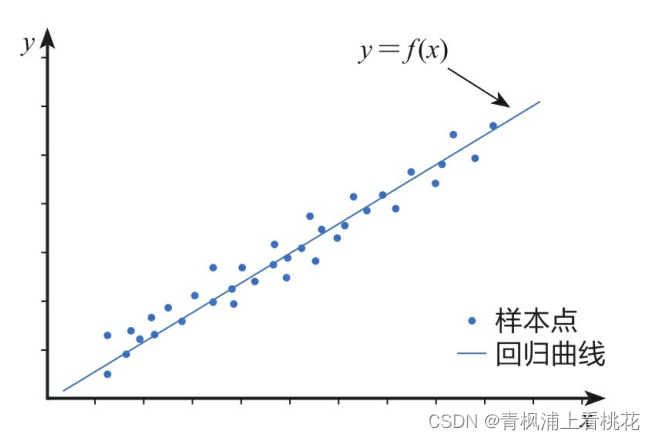
在线性回归中,我们根据特征变量(也称自变量)来预测反应变量 (也称因变量)。根据特征变量的个数可将线性回归模型分为一元线性回归和多元线性回归。
2.数学中一元线性回归的数学原理
一元线性回归模型又称为简单线性回归模型,其形式可以表示为如 下所示的公式。
y=ax+b
其中,y为因变量,x为自变量,a为回归系数,b为截距。
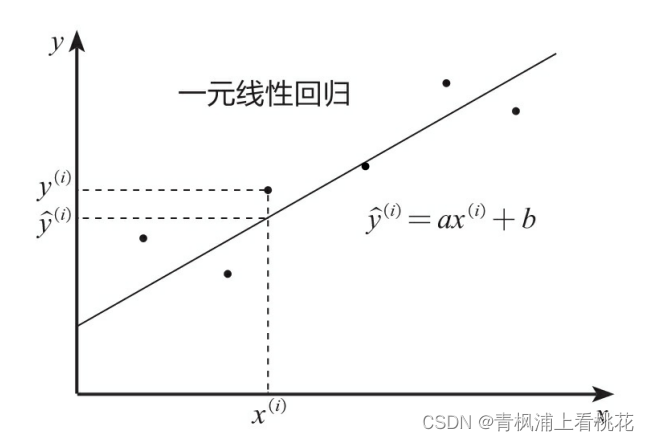
如下图所示,其中y(i)为实际值, 为预测值,一元线性回归的 目的就是拟合出一条线来使得预测值和实际值尽可能接近,如果大部分 点都落在拟合出来的线上,则该线性回归模型拟合得较好。
二、一元线性回归的python实现代码
1.绘制散点图
首先利用之前学过的Matplotlib库绘制几个散点,代码如下。
import matplotlib.pyplot as plt
X = [[1], [2], [4], [5]]
Y = [2, 4, 6, 8]
plt.scatter(X, Y)
plt.show()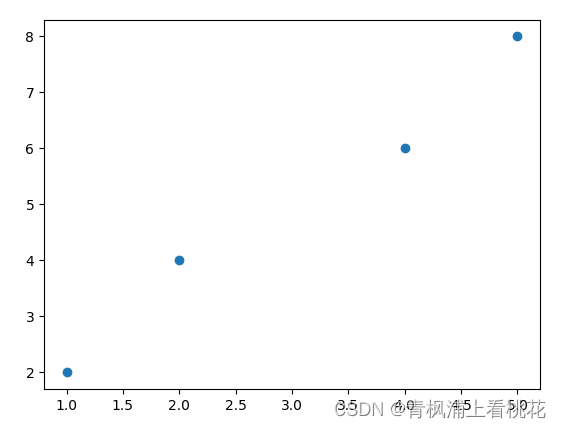
需要注意的是,这里的自变量集合要写成二维结构形式,即大列表 里包含小列表。这一点其实是符合之后要学习的多元回归的逻辑的,因 为在多元回归中,一个因变量Y可能对应多个自变量X。例如,三元线 性回归(即有3个特征变量)的自变量集合X就要写成类似如下形式。
X = [[1, 2, 3], [2, 4, 5], [4, 6, 8], [5, 7, 9]]
2.引入Scikit-Learn库搭建模型
有了原始数据后,引入Scikit-Learn库便可快速搭建线性回归模型, 代码如下。
from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X, Y)第1行代码从Scikit-Learn库引入线性回归的相关模块 LinearRegression;
第2行代码构造一个初始的线性回归模型并命名为 regr;
第3行代码用fit()函数完成模型搭建,此时的regr就是一个搭建好的线性回归模型。
3.模型预测
接着就可以利用搭建好的模型regr来预测数据。假设自变量是1.5, 那么使用predict()函数就能预测对应的因变量y,代码如下。
y = regr.predict([[1.5]])
注意这里的自变量还是要写成二维结构形式。获得的预测结果y为 一个一维数组,其内容如下。
[2.9]
如果想同时预测多个自变量,则可以使用如下代码。
y = regr.predict([[1.5], [2.5], [4.5]])
预测结果如下。
[2.9 4.3 7.1]
4.模型可视化
还可以将搭建好的模型以可视化的形式展示出来,代码如下。
plt.scatter(X, Y)
plt.plot(X, regr.predict(X))
plt.show()绘制效果如下图所示,此时的一元线性回归模型就是中间形成的一 条直线。
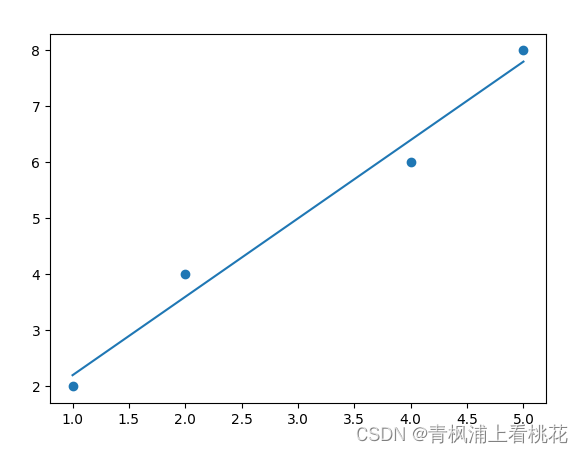
5.线性回归方程构造
通过coef_和intercept_属性可以得到此时趋势线的系数和截距,代 码如下。
print('系数a:' + str(regr.coef_[0]))
print('截距b:' + str(regr.intercept_))
因为通过regr.coef_获得的是一个列表,所以要通过regr.coef_[0]选 取其中的元素,又因为该元素为数字,所以进行字符串拼接时需要利用 str()函数将其转换成字符串,运行结果如下。
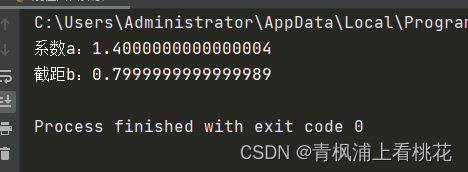
因此,拟合得到的一元线性回归方程为y=1.4x+0.8。
三、实战不同行业工龄与薪水的线性回归模型
1.读取数据并查看前五条
import pandas as pd
df = pd.read_excel('F:\\dada-bishe\\IT行业收入表.xlsx')
df.head( )
print(df.head( ))

2.对工龄和薪水赋值并打印结果
X = df[['工龄']]
Y = df['薪水']
print(X)
print(Y)打印结果省略
3.绘制散点图对数据进行简单分析
画图的目的是为了分析数据的分布情况及其特点,方便选取合适的的算法,建立合理的模型,进一步用模型对新的数据进行预测。
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.scatter(X, Y)
plt.xlabel('工龄')
plt.ylabel('薪水')
plt.title('不同工龄的薪水分布情况\n')
plt.show()

4.建模
from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X, Y)
5.模型可视化
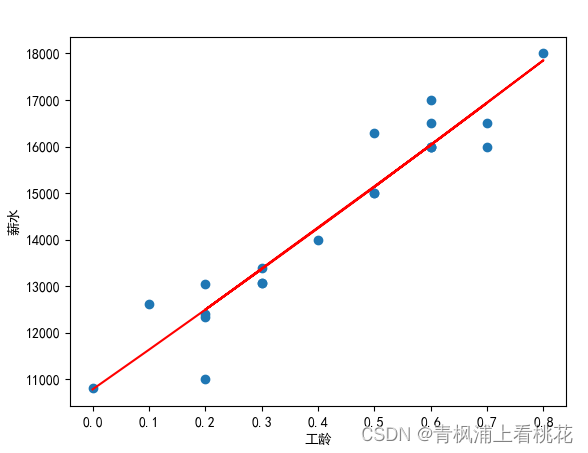
plt.scatter(X, Y)
plt.plot(X, regr.predict(X), color='red')
plt.xlabel('工龄')
plt.ylabel('薪水')
plt.show()

6.线性回归方程构造
print('系数a:' + str(regr.coef_[0]))
print('截距b:' + str(regr.intercept_))系数a:8837.375954198473
截距b:10733.350190839696
因此,拟合得到的一元线性回归方程为y=8837x+ 10733。
7.模型优化
一元线性回归模型其实还有一个进阶版本——一元多次线性回归模 型,比较常见的是一元二次线性回归模型,其形式可以表示为如下所示 的公式。
y=ax^2+bx+c
之所以还需要研究一元多次线性回归模型,是因为有时真正契合的 趋势线可能不是一条直线,而是一条曲线。如下图所示,根据一元二次 线性回归模型绘制的曲线更契合散点图呈现的数据变化趋势。
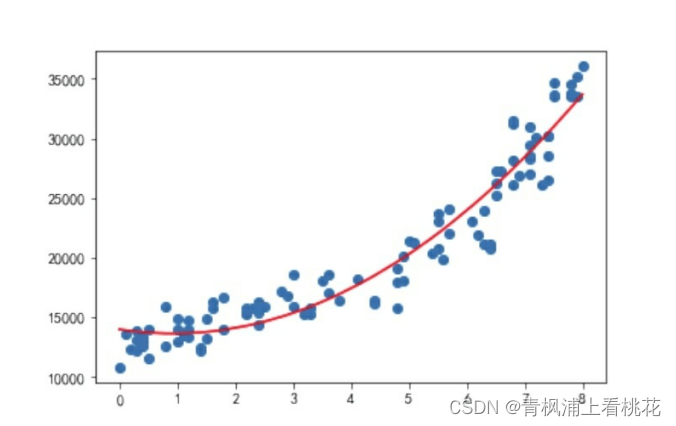
那么如何在Python中搭建一个一元二次线性回归模型呢?
首先,通 过如下代码生成二次项数据。
from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree=2)
X_ = poly_reg.fit_transform(X)第1行代码引入用于增加一个多次项内容的模块 PolynomialFeatures。
第2行代码设置最高次项为二次项,为生成二次项数据(x 2)做准 备。
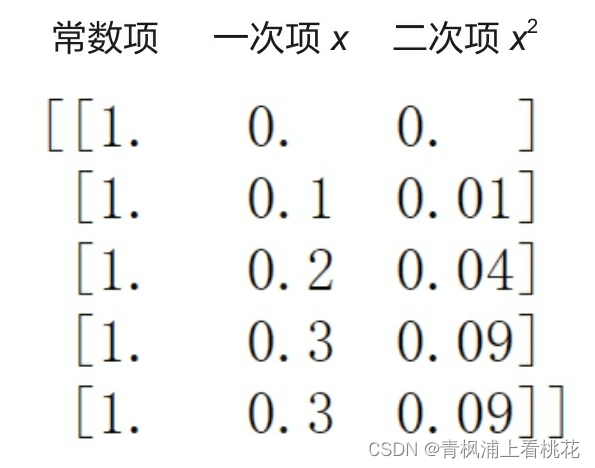
第3行代码将原有的X转换为一个新的二维数组X_,该二维数组包 含新生成的二次项数据(x 2)和原有的一次项数据(x)。
X_的内容为如下图所示的一个二维数组,其中第1列数据为常数项 (其实就是x 0),没有特殊含义,对分析结果不会产生影响;第2列数 据为原有的一次项数据(x);第3列数据为新生成的二次项数据(x^2)。
import pandas as pd df = pd.read_excel('F:\\dada-bishe\\IT行业收入表.xlsx') # print(df.head( )) X = df[['工龄']] Y = df['薪水'] from matplotlib import pyplot as plt plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 from sklearn.preprocessing import PolynomialFeatures poly_reg = PolynomialFeatures(degree=2) X_ = poly_reg.fit_transform(X) from sklearn.linear_model import LinearRegression regr = LinearRegression() regr.fit(X_, Y) plt.scatter(X, Y) plt.plot(X, regr.predict(X_), color='red') plt.xlabel('工龄') plt.ylabel('薪水') plt.show()
到这里也许会问到这也没优化啊,跟上面的不是一样的吗,其实并不是所有的模型都需要优化的,对于本案例模型就很好了,所以优不优化得看实际情况,具体情况具体分析。
print(regr.coef_) # 获取系数a、b
print(regr.intercept_) # 获取常数项c
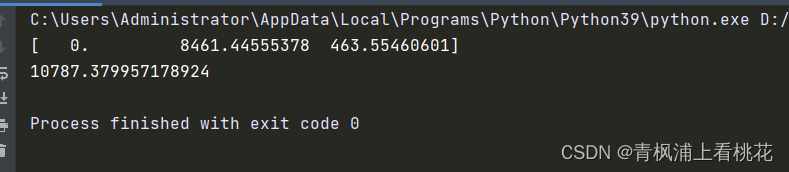
第1行为系数,有3个数:第1个数0对应X_中常数项的系数,这也 是为什么之前说X_的常数项不会对分析结果产生影响;
第2个数对应X_ 中一次项(x)的系数,即系数b;
第3个数对应X_中二次项(x 2)的系 数,即系数a。
第2行的数对应常数项c。
因此,拟合得到的一元二次线 性回归方程为y=463x 2 +8461x+10787。
四.线性回归模型评估
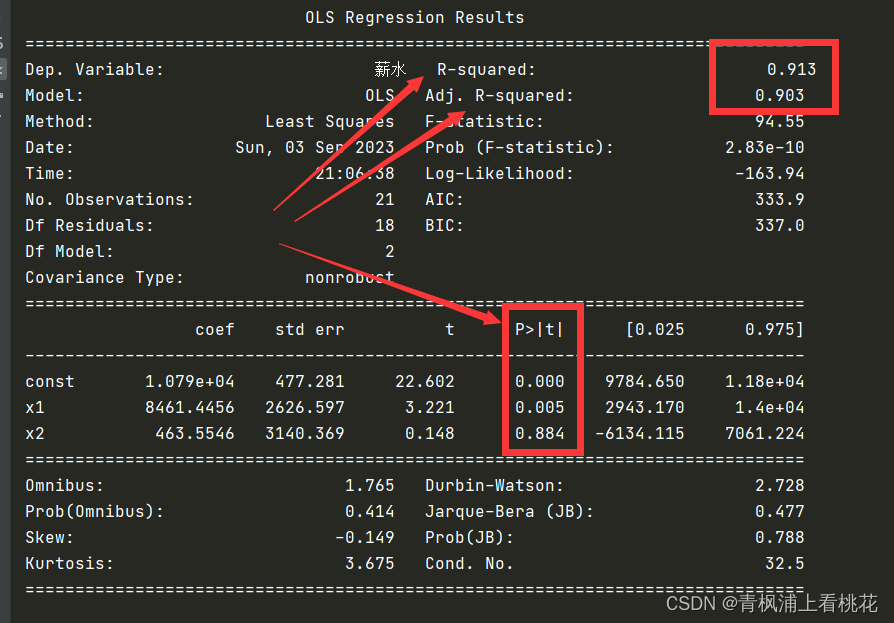
模型搭建完成后,还需要对模型进行评估,这里主要以3个值作为 评判标准:R-squared(即统计学中的R 2)、Adj.R-squared(即Adjusted R 2)、P值。其中R-squared和Adj.R-squared用来衡量线性拟合的优劣,P 值用来衡量特征变量的显著性
1.模型评估的编程实现
因为模型评估的数学原理比较复杂,而这里侧重于实战应用,所以这里先讲解在实战中如何通过编程来评估模型。 在实战应用中,我们只需要记住这两条规则:R-squared和Adj.Rsquared的取值范围为0~1,它们的值越接近1,则模型的拟合程度越高;
P值在本质上是个概率值,其取值范围也为0~1,P值越接近0,则 特征变量的显著性越高,即该特征变量真的和目标变量具有相关性。
2.实现过程。
import statsmodels.api as sm
X2 = sm.add_constant(X_)
est = sm.OLS(Y, X2).fit()
print(est.summary()) 第1行代码引入用于评估线性回归模型的statsmodels库并简写为 sm。
第2行代码用add_constant()函数给原来的特征变量X_添加常数项,并 赋给X2,这样才有y=ax+b中的常数项,即截距b,注意Scikit-Learn库 不需要这一步。
第3行代码用OLS()和fit()函数对Y和X2进行线性回归方程搭建。
第4行代码打印输出该模型的数据信息,如下图所示
 五.多元线性回归
五.多元线性回归
1.多元线性回归的数学原理和代码实现
多元线性回归模型可以表示为如下所示的公式。
````
其中x1、x2、x3……为不同的特征变量,k1、k2、k3……则为这些 特征变量前的系数,k0为常数项。多元线性回归模型的搭建也是通过数 学计算来获取合适的系数,使得如下所示的残差平方和最小,其中 y(i)为实际值, 为预测值。
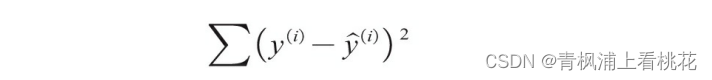
2.实现原理及代码
其实现原理跟实现的核心代码跟一元线性回归方程一样,略,这里只给出数据样列和参考代码。
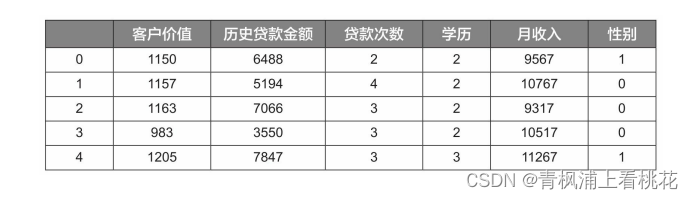























 947
947











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










