目录
1 微分中值定理
1.1 罗尔定理（Rolle）
答题步骤：
例题：
1.2 拉格朗日中值定理（Lagrange）
例题：
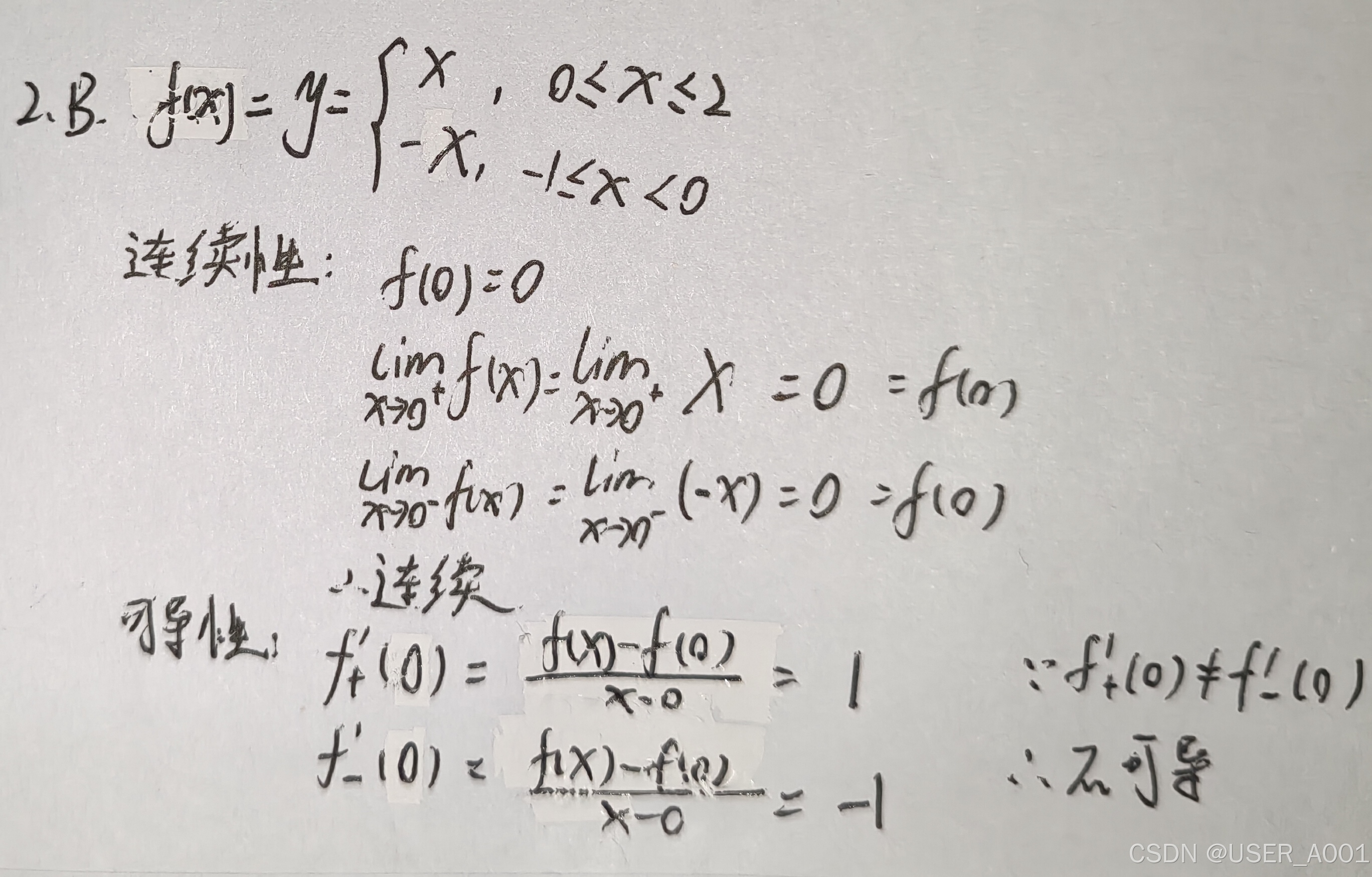
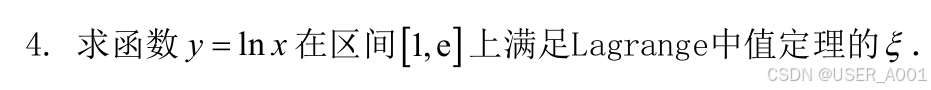
1.3 柯西中值定理（Cauchy）
2 洛必达法则（求极限）
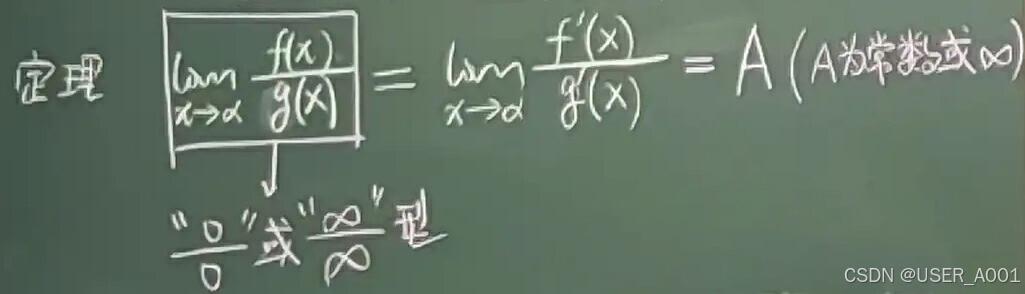
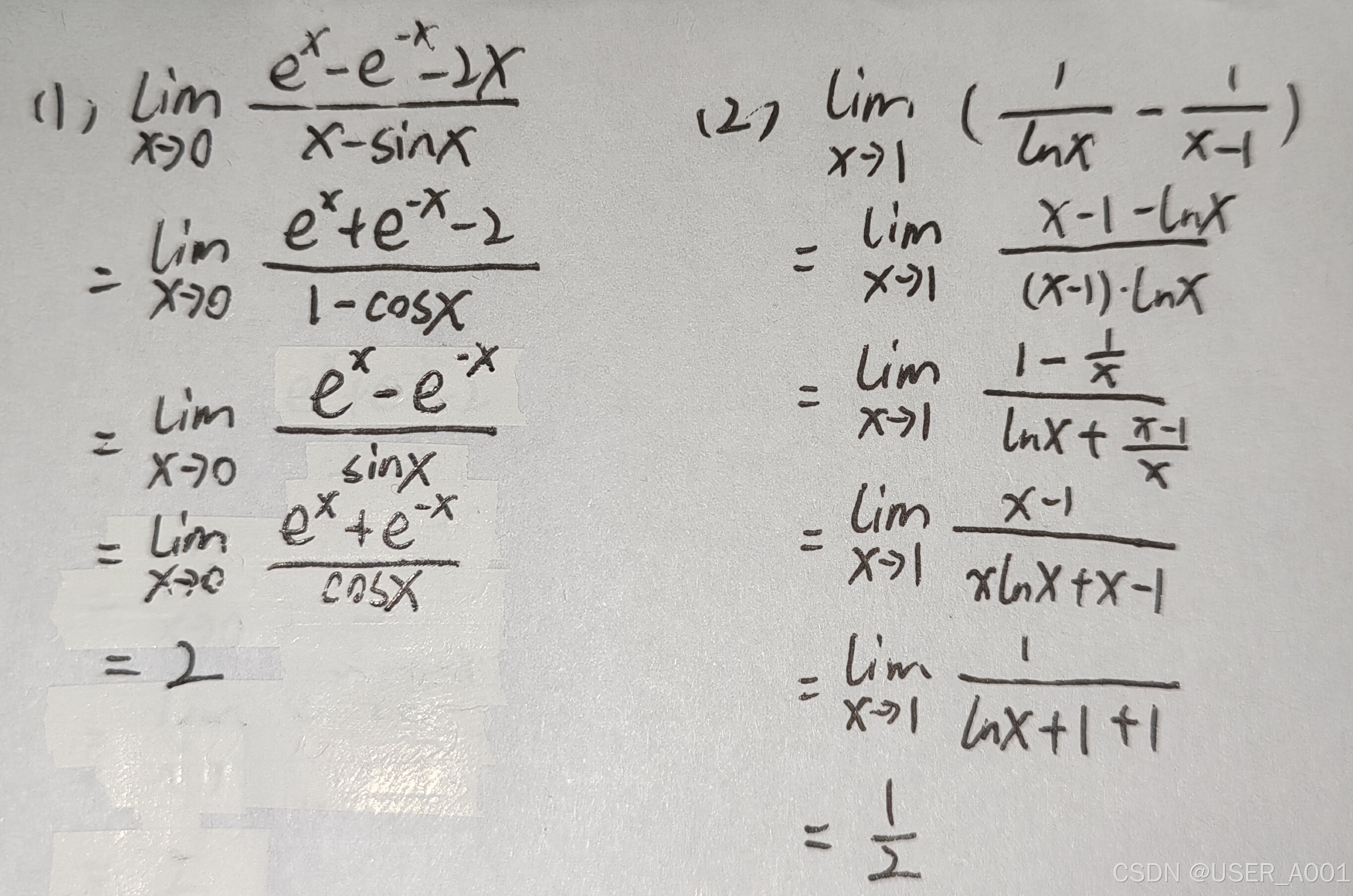
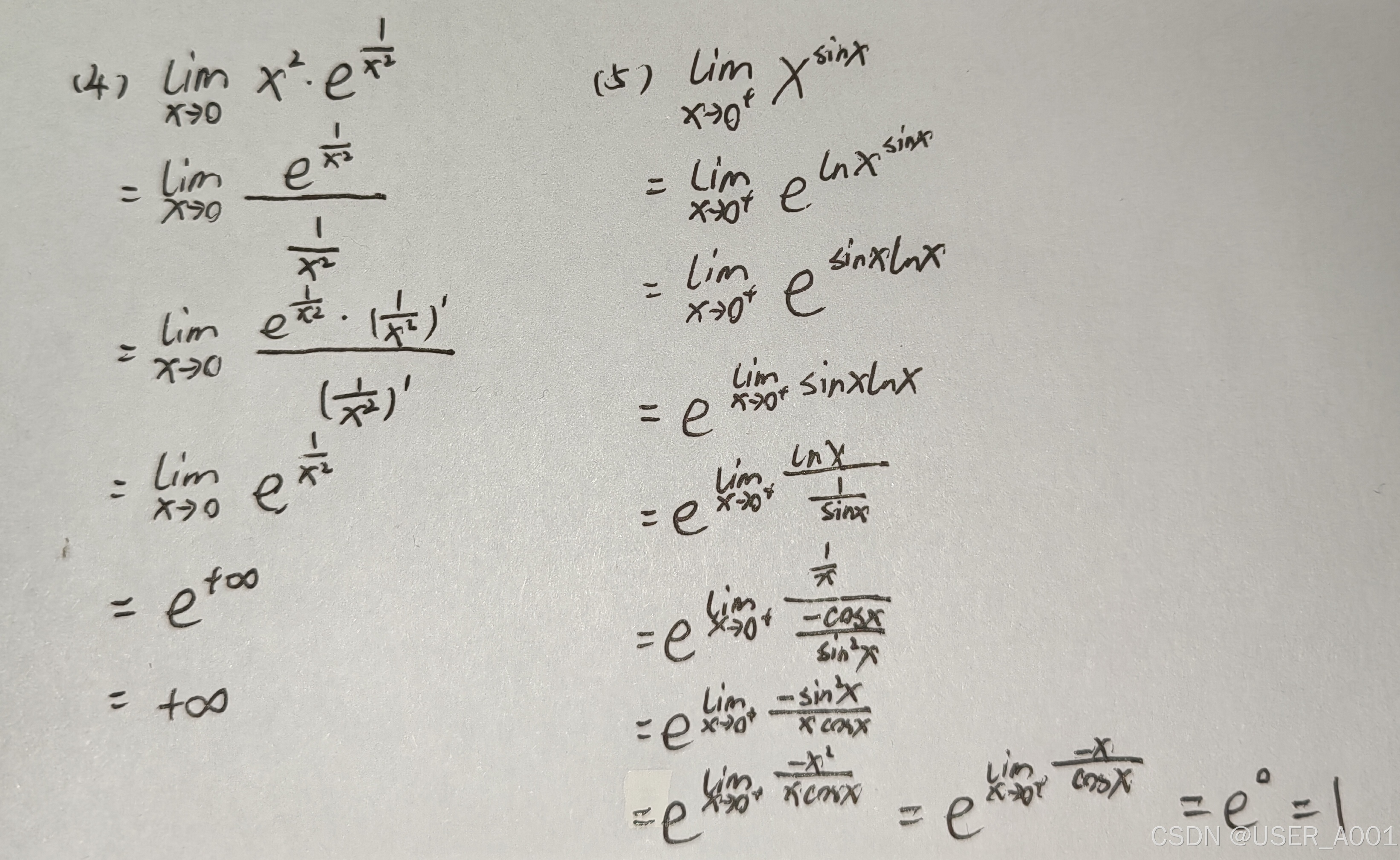
3 泰勒公式
暂无相关内容（不考不学，嘿嘿）
4 函数的单调性与极值
4.1 常规方法
例题：
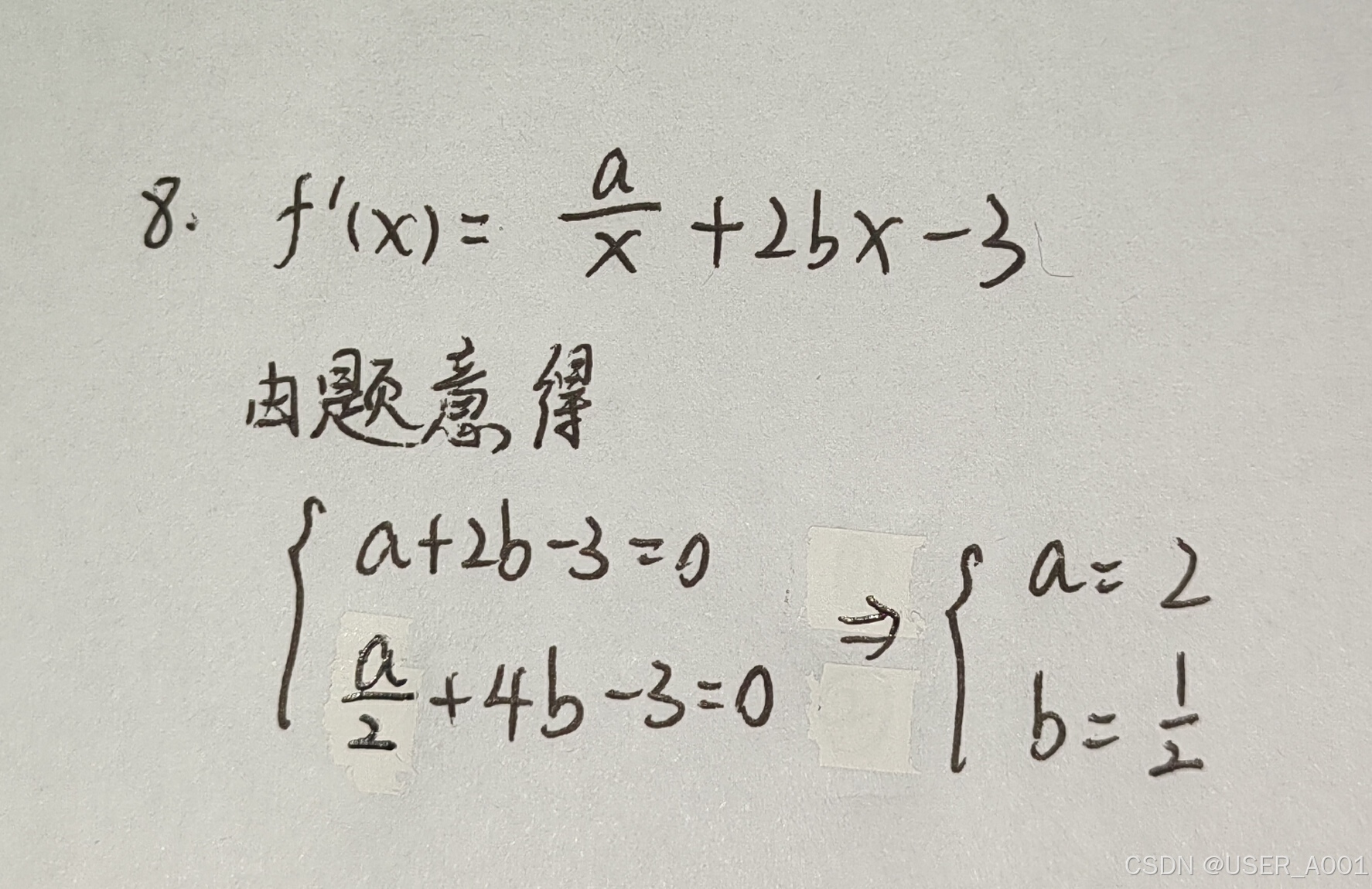
4.2 特殊方法
通过二次求导直接判断极值
注意点：适用一阶导数为0且二阶导数不为零的点
例题：
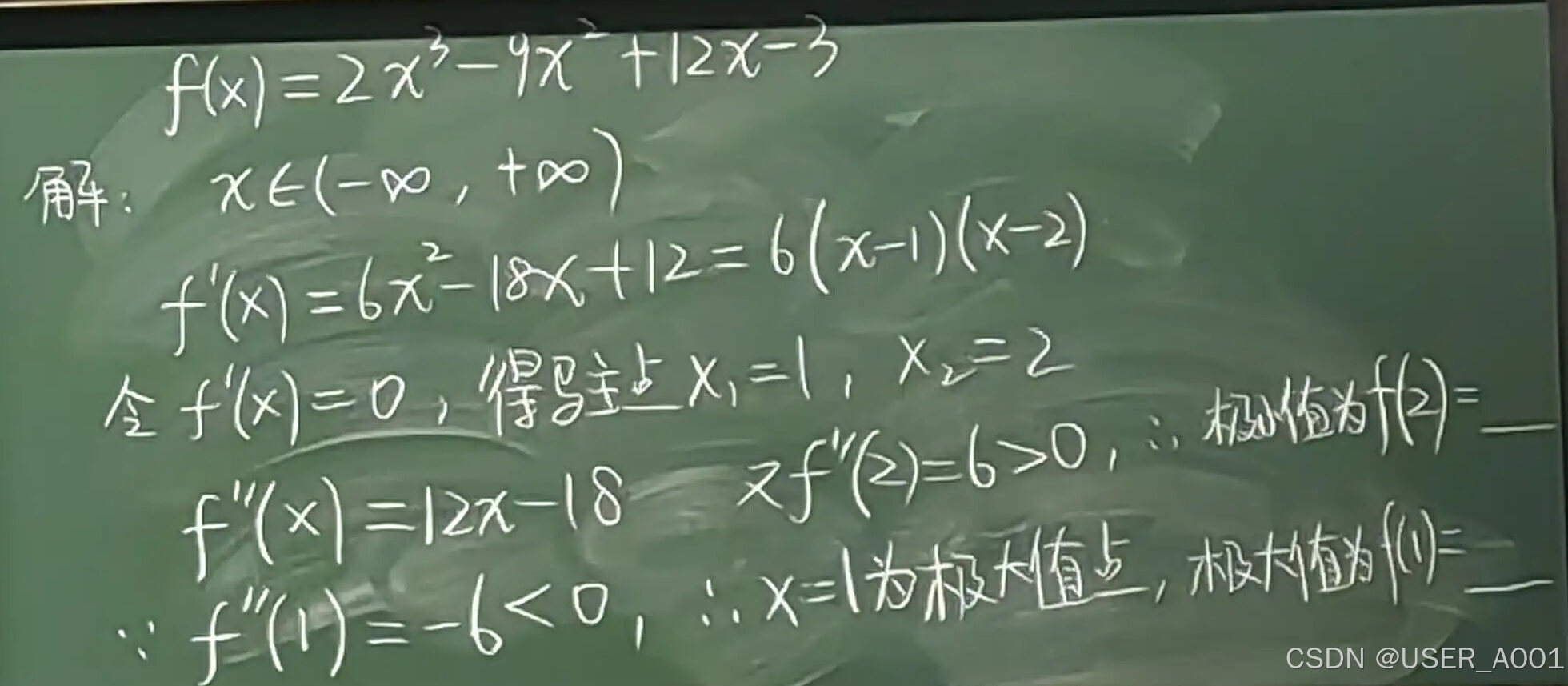
5 曲线的凹凸性与拐点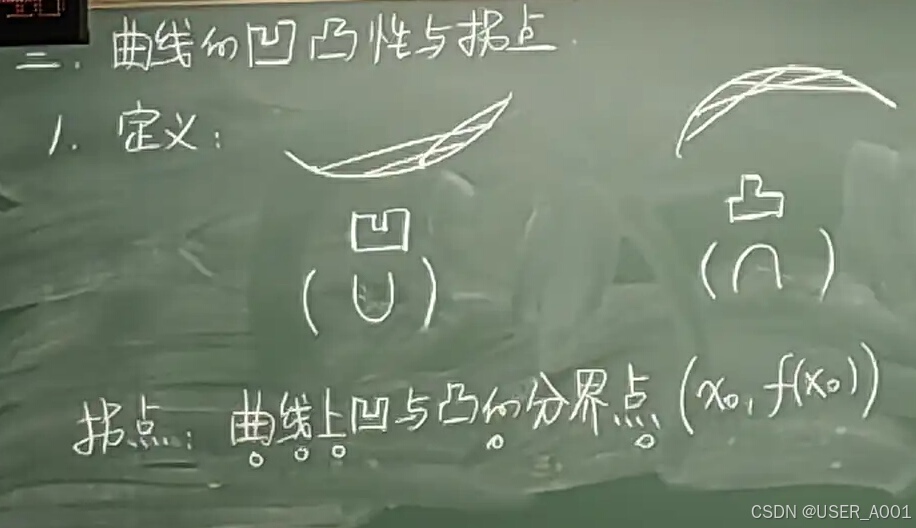 
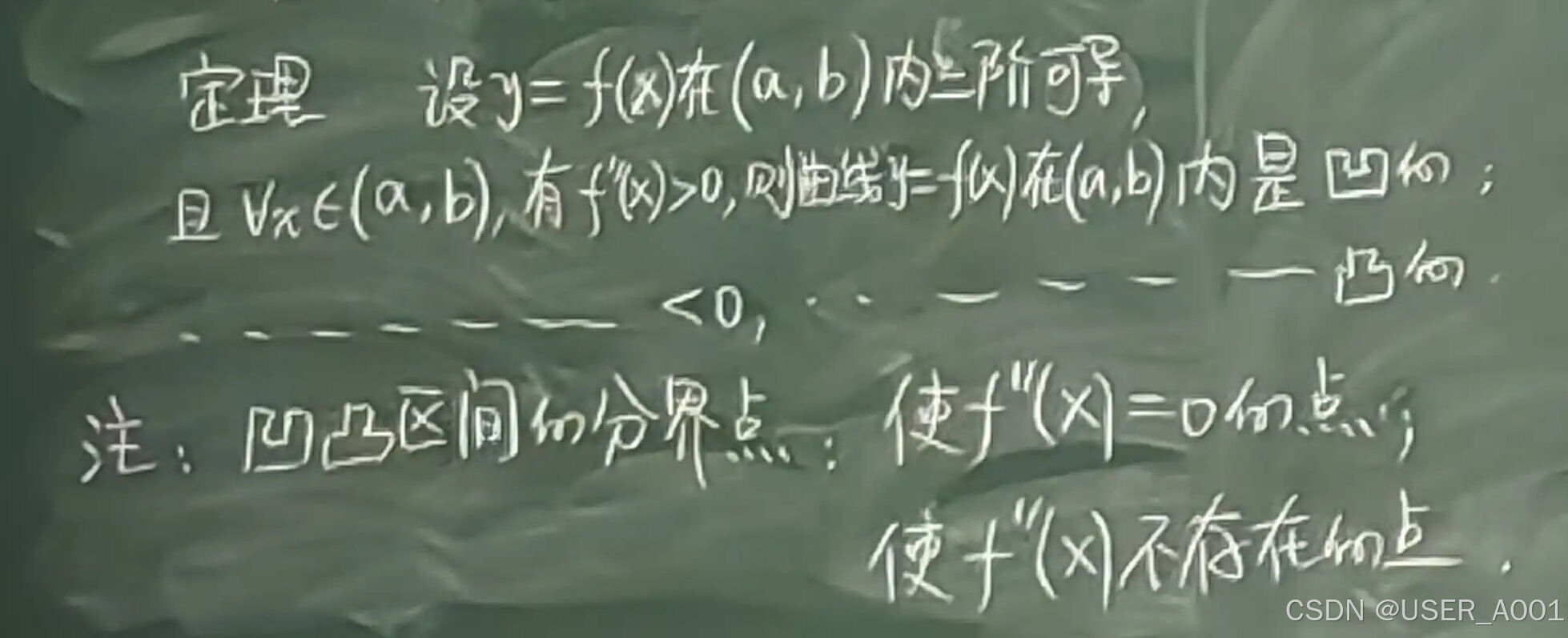
注意判断是否是拐点：凹凸区间分界点
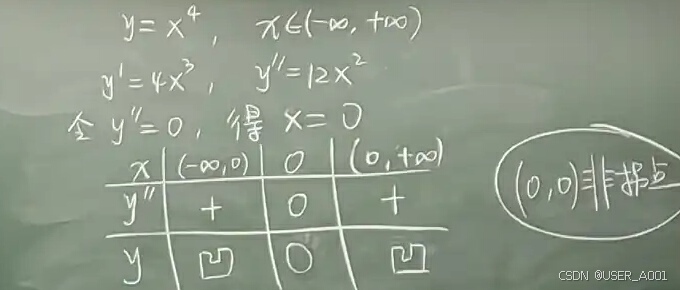
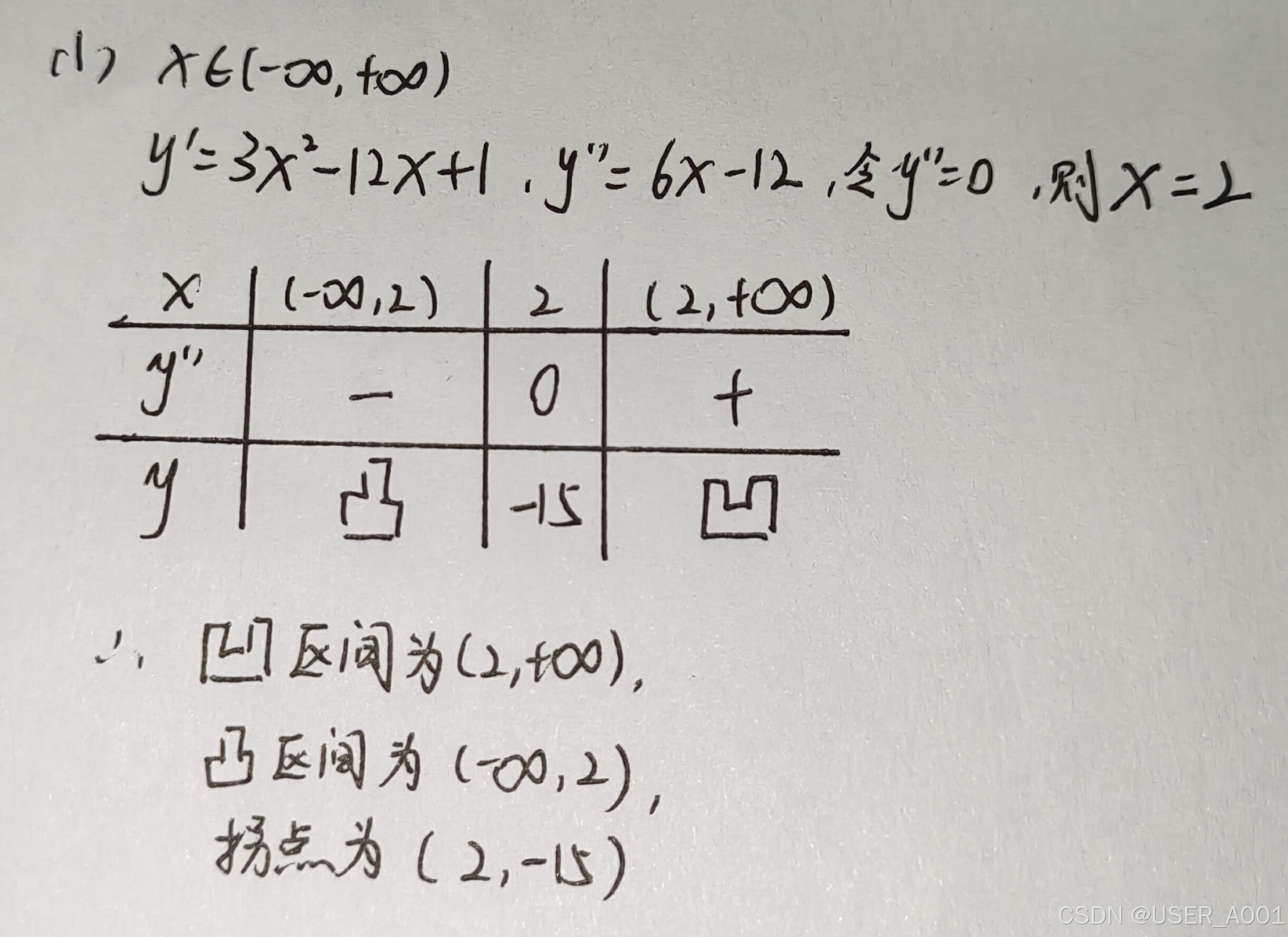
例题：
6 函数的最值
6.1 闭区间求最值
直接比较端点值与极值点对应的函数值
例题：
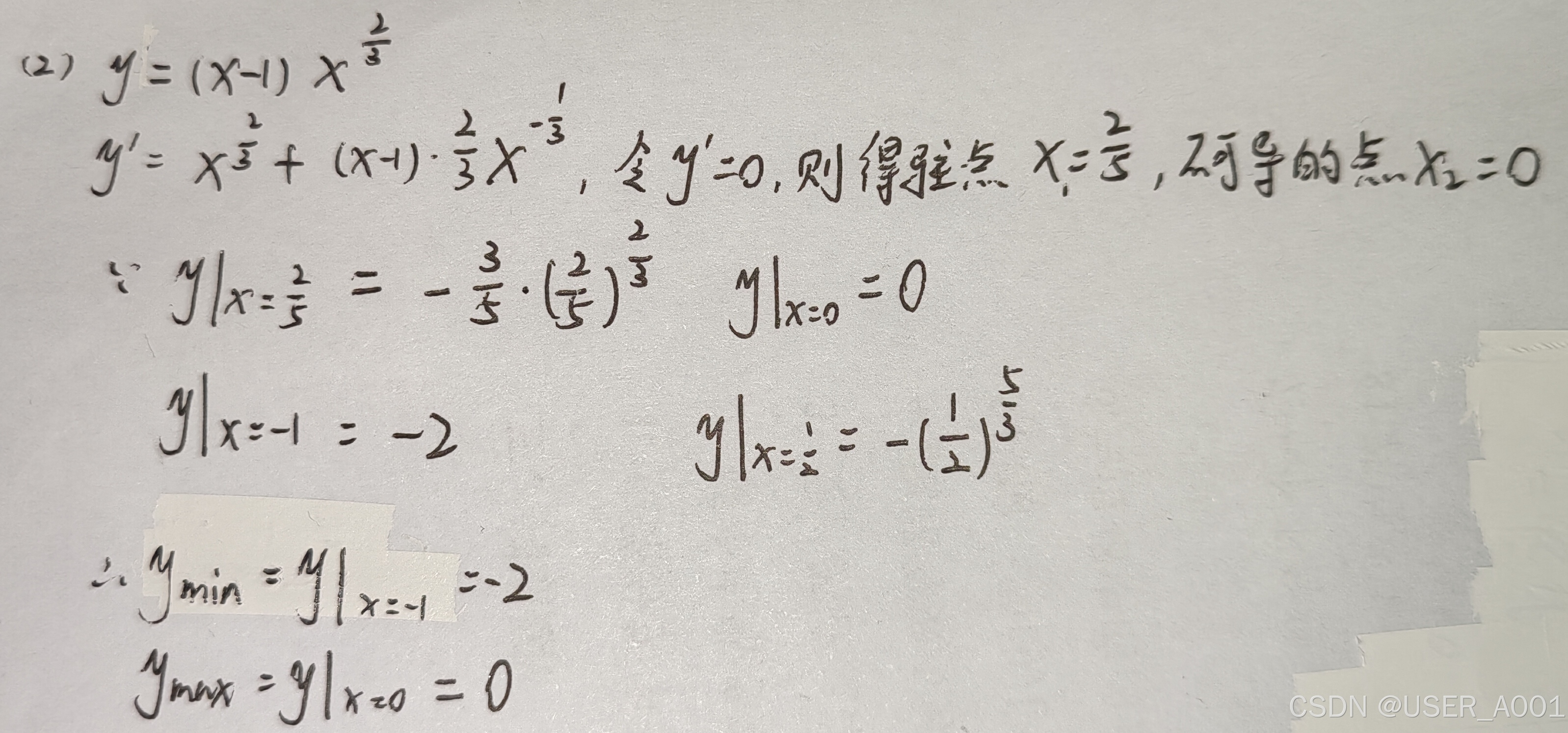
6.2 开区间求最值
唯一的极值就是最值
7 介值定理
例题：
8 曲线的渐近线
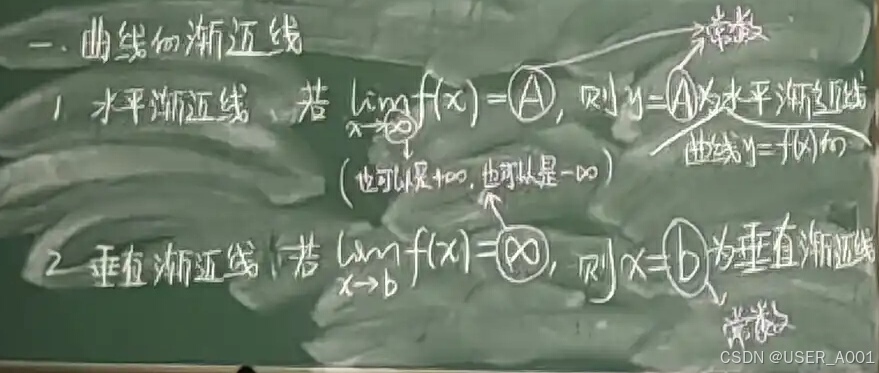例题：
扫一扫
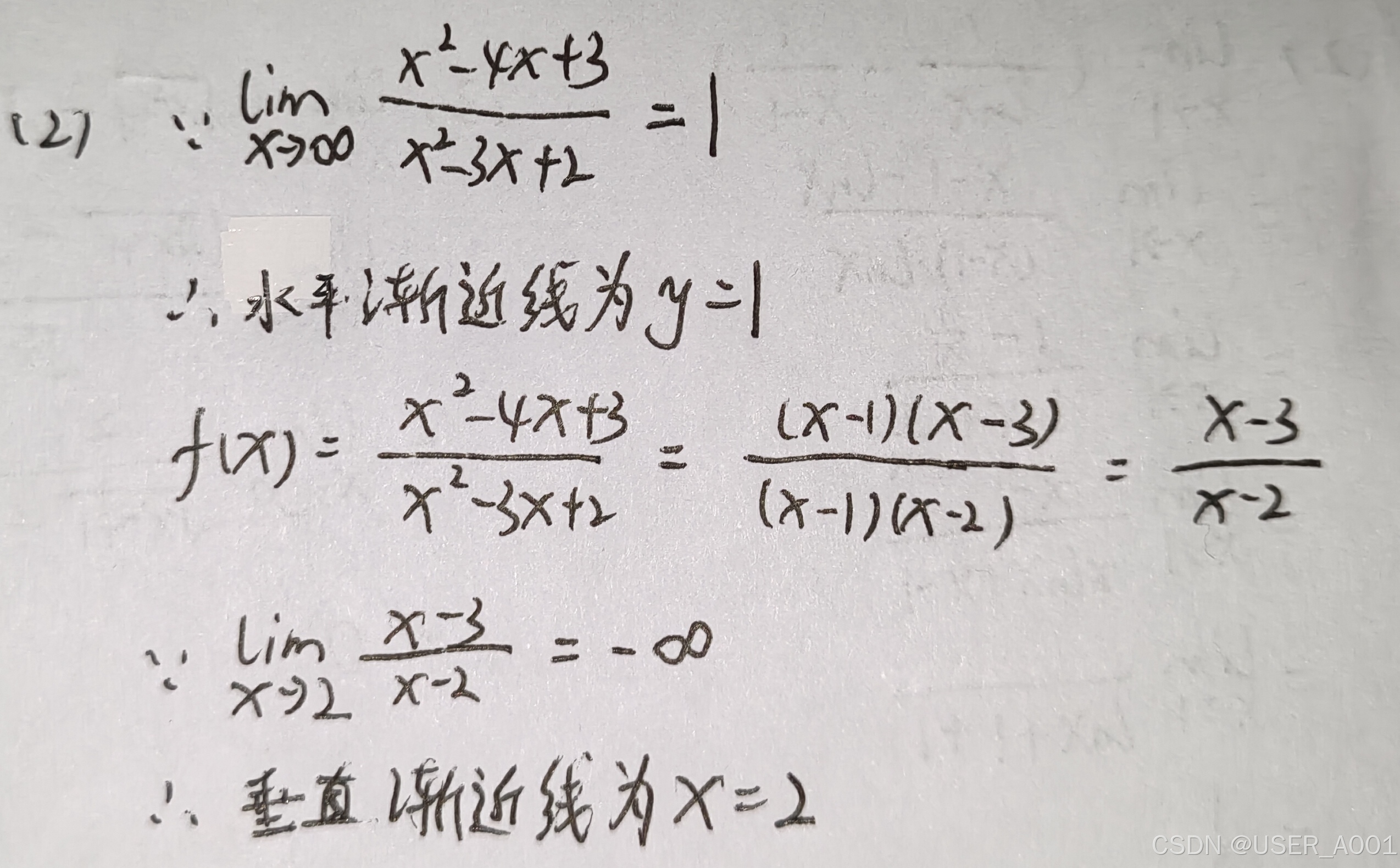
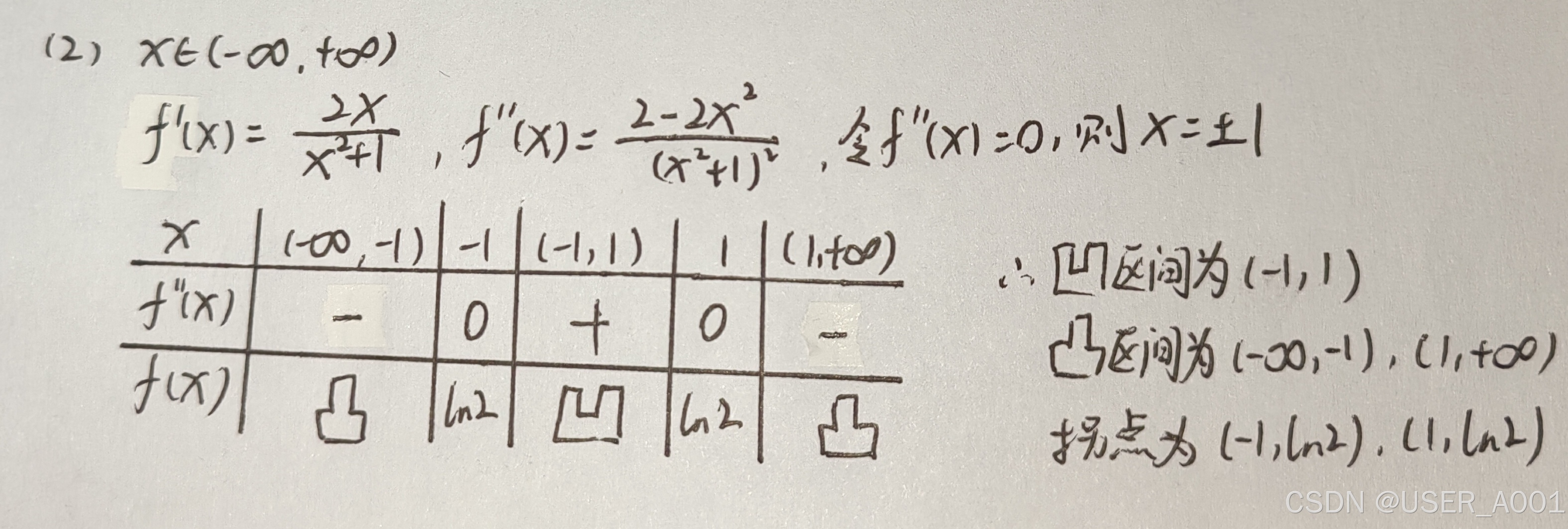
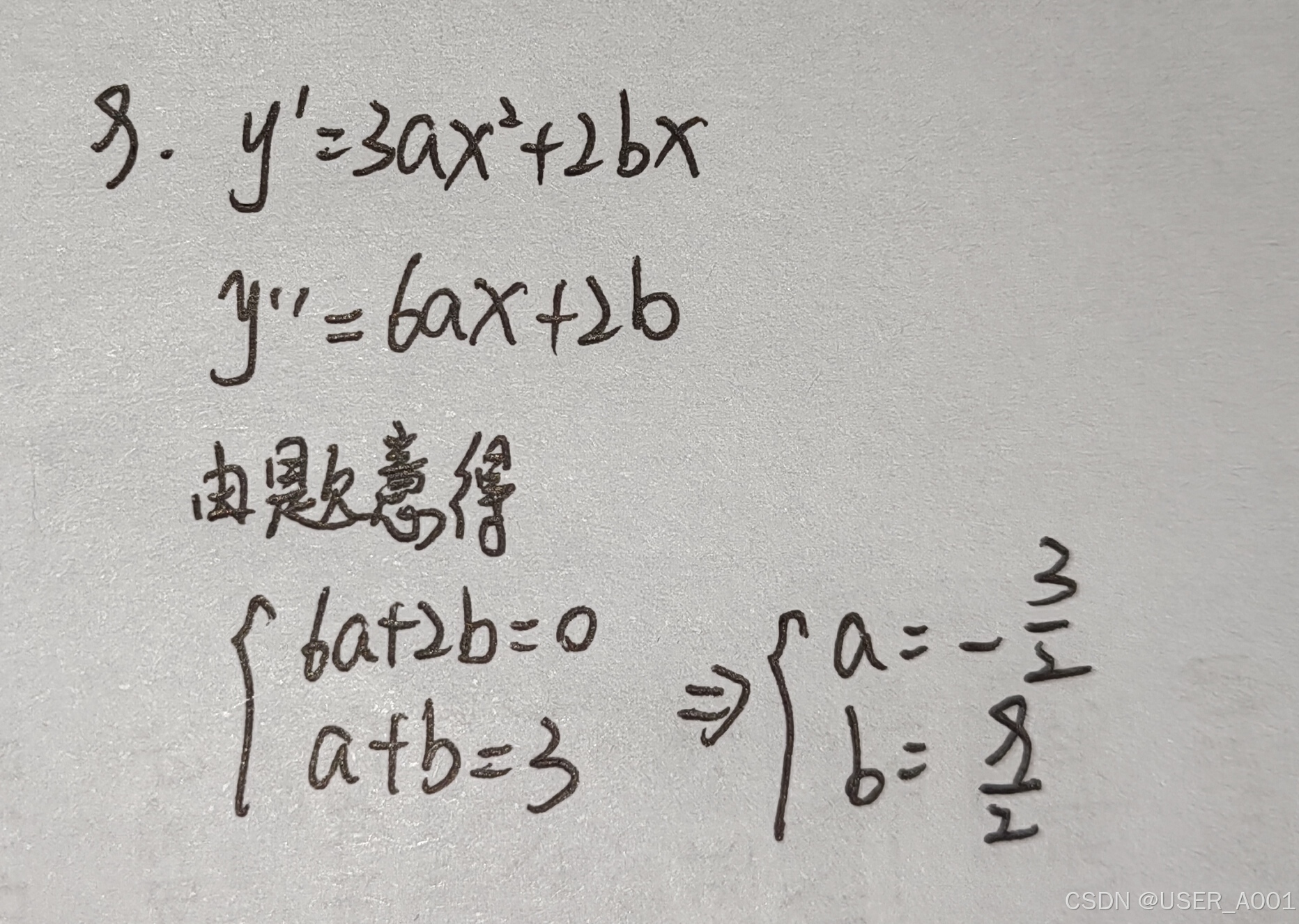
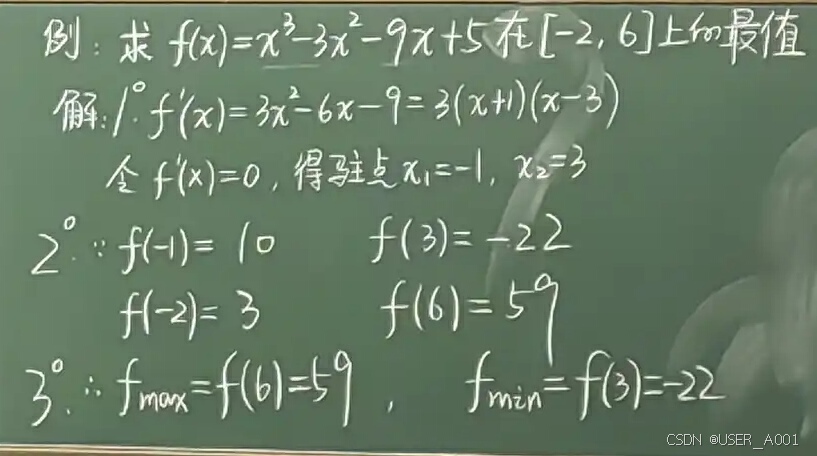
865
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
