根号分治

K-Tokitsukaze and Synthesis and Traits_2023牛客寒假算法基础集训营2 (nowcoder.com)

题意：给我们一些数对，例如（1， 2），（2， 3），（2， 4）...，然后q次询问，每次询问给我们k个数，问k个数里能凑出多少个已给数对。

我们可以抽象成无向图，数对是图上的边，然后给我们k个图上的点，问这k个点里有多少个原图上的边。

可以直接暴力吗？ 是不可以的。反例：菊花图。 例如一个点连了1e5条边，然后q（2e5）次询问每次都询问这个点，那么复杂度是2e5 * 1e5 会直接超时。

但是从这点上也启发了我们，按照一个点在原图里的度，分成大点和小点，d(x) > sqrt(n) 的是大点，d(x) <= sqrt(n) 的是小点，然后边我们可以分成3类，小小，小大，大大 。

大点确实出边很多，我们不能枚举它的所有出边，但是我们确定了是大大边，大点最多只有根号n个，大点出边(与大点相连)最多根号n个。

解释一下为什么“大点最多只有根号n个”，

可以看到点数n最大2e5，当它是完全图时边数是n*(n-1)/2 是1e10级别的，但是题目中说了边数m是小于等于2e5的，当一个图是完全图的时候，它的大点肯定是最多的，此时 n*(n-1)/2 <= 2e5，即n <= sqrt(n), 所以说大点最多根号n个。

我们可以看下图，当n=4时，大点可以有4个 > sqrt(n)。 所以说大点最多只有根号n个是说当m=2e5时，大点个数最多 sqrt(n)=500个。所以jiangly大佬直接将B设置成一个固定的数，constexpr int B = 400。

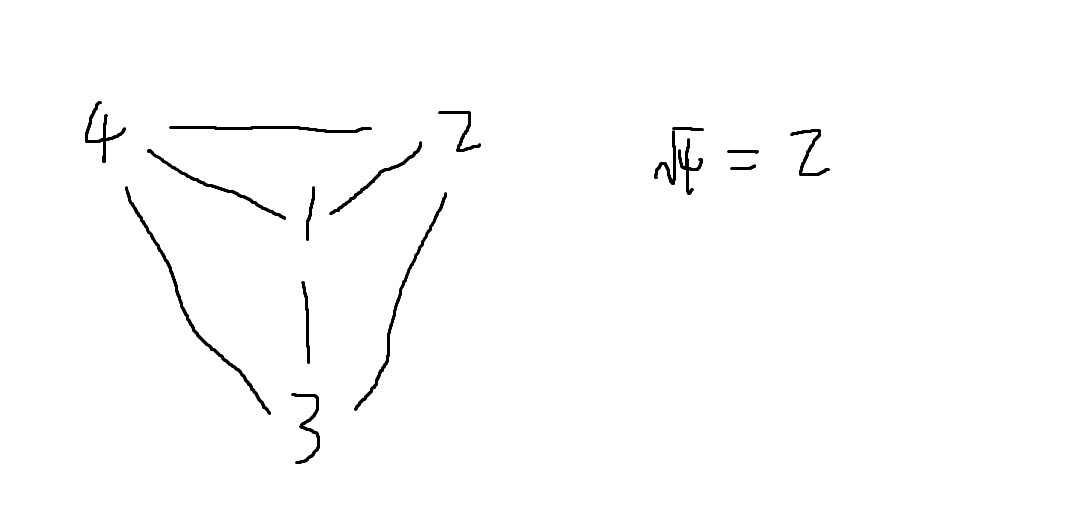
所以我们枚举每个点的邻点的个数就让我们控制在了sqrt(n)内，所以复杂度就是O(n)。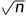

代码：

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
typedef pair<int, int>PII;
const int N = 2e5 + 100;
int n, m, q;
PII ab[N];
int a[N], deg[N];
vector<int>G[N];
bool st[N];
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
 
    cin >> n >> m >> q;
    int B = sqrt(n) + 1;
    for(int i = 1; i <= m; i++)
    {
        int a, b;
        cin >> a >> b;
        ab[i] = {a, b};
        deg[a]++, deg[b]++;
    }
    for(int i = 1; i <= m; i++)
    {
        int x = ab[i].first, y = ab[i].second;
        if(deg[x] <= B) G[x].push_back(y); // 小小，小大
        else {
            if(deg[y] > B) G[x].push_back(y); // 大大
        } 
        if(deg[y] <= B) G[y].push_back(x); // 小小，小大
        else {
            if(deg[x] > B) G[y].push_back(x); // 大大
        }
    }
    while(q--)
    {
        int k;
        cin >> k;
        for(int i = 1; i <= k; i++)
        {
            cin >> a[i];
            st[a[i]] = 1;
        }
        int ss = 0, sb = 0, bb = 0;
        for(int i = 1; i <= k; i++)
        {
            int x = a[i];
            if(deg[x] <= B) {
                for(int i = 0; i < G[x].size(); i++) {
                    int y = G[x][i];
                    if(st[y]) {
                        if(deg[y] <= B) ss++; // 小小
                        else sb++; // 小大
                    }
                }
            } else {
                for(int i = 0; i < G[x].size(); i++) {
                    int y = G[x][i];
                    if(st[y]) {
                        bb++; // 大大
                    }
                }
            }
        }
        cout << ss / 2 + sb + bb / 2 << endl;
        for(int i = 1; i <= k; i++) st[a[i]] = 0;
    }
 
 
    return 0;
}