leetcode刷题记录--P733 图像渲染

题目描述：

有一幅以 m x n 的二维整数数组表示的图画 image ，其中 image[i][j] 表示该图画的像素值大小。你也被给予三个整数 sr ,  sc 和 color 。你应该从像素 image[sr][sc] 开始对图像进行上色 填充 。

为了完成 上色工作：

1. 从初始像素开始，将其颜色改为 color。
2. 对初始坐标的 上下左右四个方向上 相邻且与初始像素的原始颜色同色的像素点执行相同操作。
3. 通过检查与初始像素的原始颜色相同的相邻像素并修改其颜色来继续 重复 此过程。
4. 当 没有 其它原始颜色的相邻像素时 停止 操作。

最后返回经过上色渲染 修改 后的图像 。

示例 1:

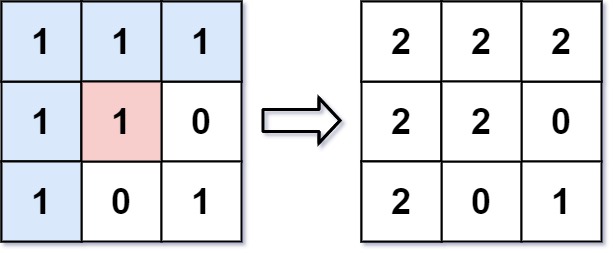
输入：image = [[1,1,1],[1,1,0],[1,0,1]]，sr = 1, sc = 1, color = 2

输出：[[2,2,2],[2,2,0],[2,0,1]]

解释：在图像的正中间，坐标 (sr,sc)=(1,1) （即红色像素）,在路径上所有符合条件的像素点的颜色都被更改成相同的新颜色（即蓝色像素）。

注意，右下角的像素 没有 更改为2，因为它不是在上下左右四个方向上与初始点相连的像素点。

解题思路：回溯法、DFS

        对于给定的点修改颜色，如果其上下左右四个位置的颜色和该点原来的颜色相同，那么也需要修改颜色，并且继续以这些被修改过后的点为中心辐射出去渲染其他的点。依据这种思想可以考虑采用深度优先遍历（DFS）。

        因为对于每个点都需要考虑其上下左右四个位置，我们可以定义一个状态偏移的数组。来简化操作。在进行位置的判断过程中，需要考虑边界问题，以这个点为中心的上下左右四个位置不一定都存在，需要将这些点排除在外。

static int p[][]=new int[][]{{1,0},{-1,0},{0,1},{0,-1}}; // 状态偏移

for(int i=0;i<4;i++){
			//利用状态偏移进行修改
			int newx=curx+p[i][0]; 
			int newy=cury+p[i][1];

        if(newx<0 || newx>=row || newy<0 || newy>=col){
				continue;
}

        同时为了保证程序不会进入死循环，我们可以定义一个二维数组flag[i][j]，flag[i][j]=1表示(i,j)这个点已经被渲染过，不需要在被渲染。

整个过程综上就是：修改当前点（i,j）的颜色，并且利用flag进行标记表示已经渲染过。对该点的上下左右四个位置进行搜寻判断，判断是否需要进行渲染。如果存在点需要渲染，接着调用函数进行上述过程。

这个函数被抽离出来就是DFS函数，我们需要的参数是image[][]表示初始给定的图画以及该图画的行数row和列数col，当前这个中心点的位置点坐标，curx和cury。标记数据:flag[][]。该点原先的颜色：oldcol。需要修改成的颜色：newcol。

static int p[][]=new int[][]{{1,0},{-1,0},{0,1},{0,-1}}; // 状态偏移
	public static void DFS(int[][]image,int curx,int cury,int[][]flag,int oldcol,int newcol,int row,int col){
		//修改当前位置颜色
		image[curx][cury]=newcol;
		//修改完做标记
		flag[curx][cury]=1;
		//上下左右四个位置进行搜寻判断
		for(int i=0;i<4;i++){
			//利用状态偏移进行修改
			int newx=curx+p[i][0]; 
			int newy=cury+p[i][1];
			
			//判断此时位置的合法性
			if(newx<0 || newx>=row || newy<0 || newy>=col){
				continue;
			}
			//判断此时位置的颜色以及是否被修改过
			if(image[newx][newy]==oldcol&&flag[newx][newy]==0	){
				DFS(image,newx,newy,flag,oldcol,newcol,row,col);
			}
		}
	}
    public static int[][] floodFill(int[][] image, int sr, int sc, int color) {
    	//如果为空，返回空
    	if(image.length==0)
    		return image;
    	int row=image.length;
    	int col=image[0].length;
    	int flag[][]=new int[row][col];//定义标记数组
    	int oldcol=image[sr][sc]; //记录原来的颜色
    	DFS(image,sr,sc,flag,oldcol,color,row,col);
    	return image;
    	 
    }