一篇文章搞懂质数——试除法判别质数、分解质因数、筛质数（埃氏筛法、线性筛法）

试除法判定质数

质数又称为素数，质数只能被自己或者1整数。例如：1,3，5,7，11，13,17,19等都是素数，他们只能被自己本身和1整除。即数字n，如果在2 ~ n-1之间都不能被n整数，那么n就是质数。那么，我们怎么通过代码来计算出这个数是不是素数呢？
思路一：
对于数字n，我们枚举2 ~ n-1，看是否有能被n整除的，如果有那么这个数就不是质数
思路二：
我们不需要像思路一那样枚举那么多次，我们只需要枚举2 ~ sqrt（n）之间的数就可以
原因：因为如果n能被2~（n-1）之间某个数整除，其两个因子必定有一个小于或等于sqrt（n），另一个大于等于sqrt（n） 。
**技巧：**在写循环的时候，我们不需要写 i <= sqrt(n)，这样的效率有点低，我们可以写成 i <= n / i，这样的效率更高

例题：

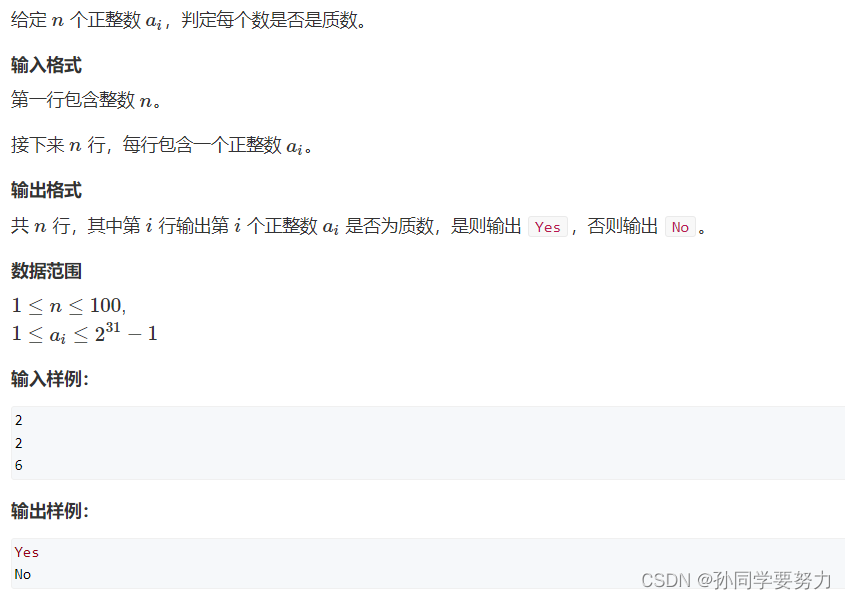
#include <iostream>

using namespace std;

bool is_prime(int x)
{
    if(x < 2) return false;//小于2的数一定不会是素数
    
    for(int i = 2; i <= x / i; i++)//枚举2 ~ sqrt(n)之间的数试除
    {
        if(x % i == 0) return false;
    }
    return true;
}

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        if(is_prime(x)) puts("Yes");
        else puts("No");
    }
    
    return 0;
}

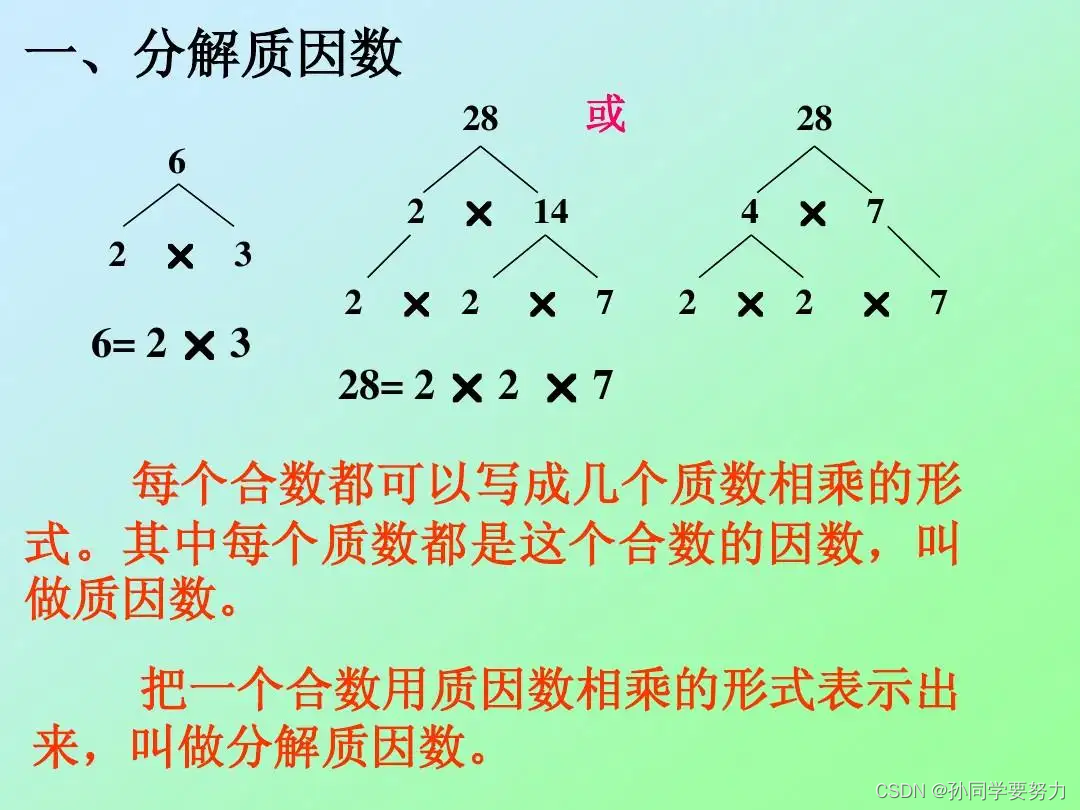
分解质因数

**算数基本定理：**不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。
即：n = p1^a1 * p2^a2 * … * pk^ak
比如一个数16 在分解时先找到2这个质因子，然后由于16/2后还可以/2，所以会在2这个质因子上产生次方

例题：

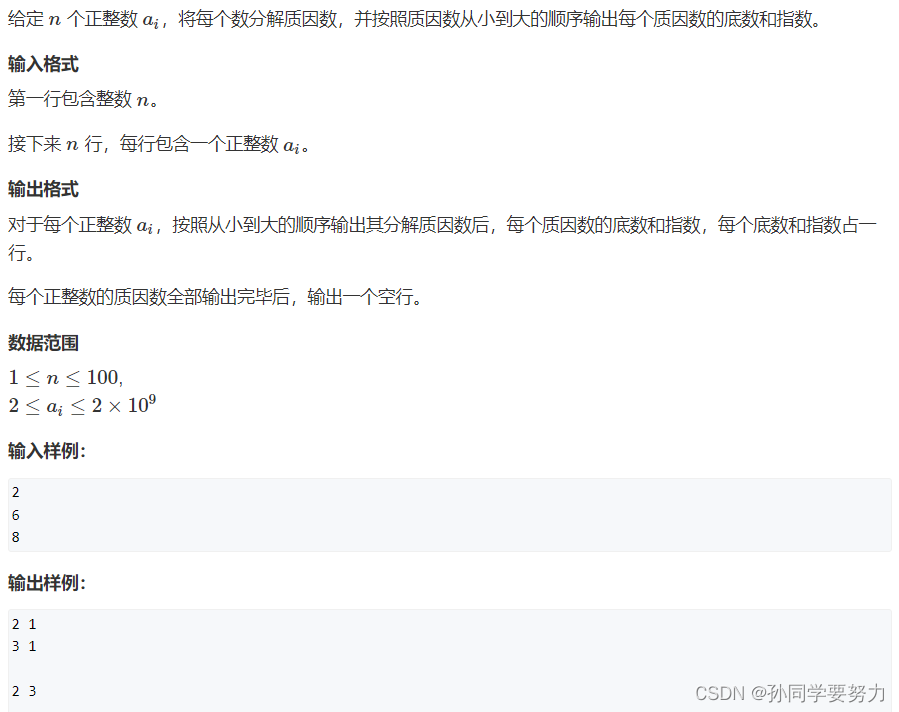
#include <iostream>

using namespace std;

int main()
{
    int n;
    cin >> n;
    
    while(n--)
    {
        int x;
        cin >> x;
        
        for(int i = 2; i <= x / i; i++)
        {
            //这里的i一定是质数，如果是合数，那么在之前的循环里面一定是被筛出来过的
            if(x % i == 0)
            {
                int s = 0;//最后的指数
                while(x % i == 0)
                {
                    x /= i;
                    s++;
                }
                cout << i << ' ' << s << endl;
            }
        }
        if(x > 1) cout << x << ' ' << 1 << endl;//x>1说明这个质因数是大于sqrt(x)的
        cout << endl;
    }
    
    return 0;
}

筛质数（重点）

筛质数的方法主要有三种：

1. 朴素版筛质数：O（nlongn）。给我们1 ~ n之间的数字，我们假如要算第i个数是不是质数，我们只要看它是不是2 ~ i-1的倍数，如果是，那么他就不是质数。 复杂度分析：2要筛 n/2 次，3要晒 n/3次…所以一共要筛 n*（1/2 + 1/3 + … + 1/n）次，后面是调和级数，当n足够大时，趋向于lnn + c，所以复杂度为 nlongn
   2.埃氏筛法：O（nlonglongn）。埃及人发明的，他和朴素版的一样，只不过把外面的那层循环加到里面，可以有效的减少时间复杂度。为什么可以加到上面呢？对于上面朴素版的筛质数，我们发现**不需要对每个数都进行筛质数，只需要对质数筛即***可**。因为任何一个合数都会被他的最小质因数筛掉，所以只需要将筛倍数的循环放到if里面即可。**复杂度分析：**1 ~ n中的质数数量是 n / lnn个，所以复杂度为 n * longlongn。
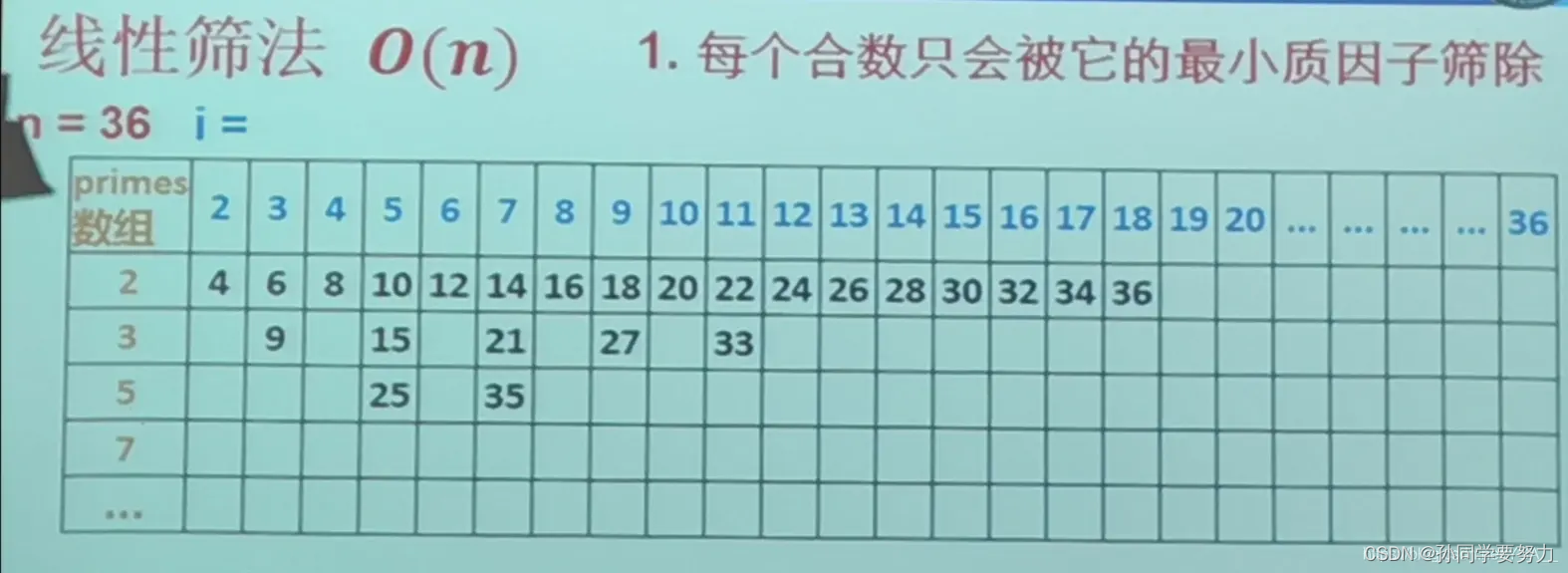
   3.线性筛法：O（n）。线性筛法核心：n只会被最小的质因子筛去。例如6在埃氏筛法中2和3都会被筛一遍，在线性筛法里面，只有2会被筛到。

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int primes[N], cnt;//数组primes用来存储质数，cnt是最后的结果，质数的总数
bool st[N];//数组st用来判断i是否是质数，如果是为false，不是为true

void get_primes1(int n)//朴素版
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i]) primes[cnt++] = i;
        for(int j = i; j <= n; j += i)//如果是i的倍数，则不是质数，赋值为true
        {
            st[j] = true;
        }
    }
}

void get_primes2(int n)//埃氏筛法
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i])
        {
            primes[cnt++] = i;
            for(int j = i; j <= n; j += i)
                st[j] = true;
        }
    }
}

void get_primes3(int n)//线性筛法
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i]) primes[cnt++] = i;
        //1.当i % pj == 0时，pj一定是i的最小质因子，因此pj一定是pj * i的最小质因子
        //2.当i % pj ！= 0时，pj一定小于i的最小质因子，因此pj一定是pj * i的最小质因子
        for(int j = 0; primes[j] <= n / i; j++)//j从小到大枚举所有质数
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;//pj就是i最小的质因数，j不再往后走了，
        }
    }
}

int main()
{
    int n;
    cin >> n;
    
    get_primes3(n);
    
    cout << cnt << endl;
    
    return 0;
}