论文阅读：关于非凸函数分布式压缩感知，分布式分的老彻底了

雾隐山前鹤

已于 2025-03-21 19:27:51 修改

阅读量191

点赞数 7

文章标签：分布式信号处理

于 2025-02-19 16:47:34 首次发布

本文链接：https://blog.csdn.net/qq_59850451/article/details/145699327

版权

非凸稀疏度量和一阶近似法

由于lasso因为正则化参数的存在总是有偏的，因此人们开始寻找比1范数更好的稀疏度惩罚函数，表示如下：

凹函数LASSO

这种优化问题的解法是在 g 的附近采用一阶线性近似求解，这是一个常规手段，表示如下

在 JSM-2 的稀疏设置当中，凹函数优化问题表示如下：

后面的惩罚项就是“联合稀疏度量”，类比 L2,1 范数就好理解了。然而这个形式表明每个 agent v 都需要获取所有参与者的信息，然后同步优化。

我们假设每个 agent 只能获得自己和邻居的信息 $\mathcal{N}_v$ 的信息，替换全局信息，则上述优化问题变为

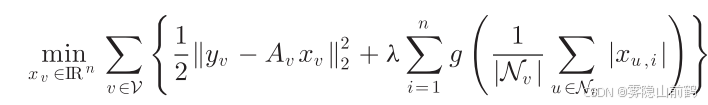
进一步，agent 之间只能传递最优 0 1 近似（要么是0要么是1），上述优化问题进一步被转换为

后面那一坨是 v 邻居的 0 1 近似的平均值， $\alpha$ 是一个调优参数，相应地该优化问题的求解器被设计为：

当 g 被设计为 MCP函数：

有

优化问题可以表示为：

注：

这个问题中包含加权 0 范数的求解，现有的方法不好应用，考虑 surrogate functional

首先定义全局问题的代理损失泛函为

定义：则易得：

那么局部子问题的代理泛函为：

经过原文讨论，该函数具有以下性质：

如果 z <= w , $\arg\min\mathcal{R}_w(x_{v,i})=0$

反之 $\arg\min\mathcal{R}_w(x_{v,i})=z_{v,i}-w_{v,i}sgn(x_{v,i})$

那么该代理函数的优化器就是一个分段的软硬阈值结合函数：

相应地，局部代理函数的更新如下：

至此就可以设计算法如下：

function [Power_Ssv] = DJ_IST_Optimized(MIX, numRX, theta, varargin)
% DJ_IST_Optimized 改进的分布式迭代收缩阈值算法
% 输入参数：
%   MIX   - 输入信号矩阵 [numRX x snapshots]
%   numRX - 接收天线数量
%   theta - 角度网格向量 (度)
%   varargin - 正则化参数 例如1.2
% 可选参数：
%   'MaxIter'   最大迭代次数 (默认10000)
%   'Epsilon'   收敛阈值 (默认1e-3)
%   'Tau'       步长参数 (默认5e-4)
%   'Lambda'    正则化参数 (默认1.4)
%   'Alpha'     权重参数 (默认5e-5)
%   'Beta'      阈值参数 (默认1.1)
%   'P'         连续零抑制参数 (默认10000)
% 输出：
%   Power_Ssv - 功率谱估计

%% 参数解析
p = inputParser;
addParameter(p, 'MaxIter', 10000, @isnumeric);
addParameter(p, 'Epsilon', 1e-3, @isnumeric);
addParameter(p, 'Tau', 5e-4, @isnumeric);
addParameter(p, 'Lambda', 1.4, @isnumeric);
addParameter(p, 'Alpha', 5e-5, @isnumeric);
addParameter(p, 'Beta', 1.1, @isnumeric);
addParameter(p, 'P', 10000, @isnumeric);
parse(p, varargin{:});
params = p.Results;

%% 过完备基矩阵构造 (向量化加速)
theta_rad = deg2rad(theta(:)'); % 转换为弧度行向量
d_lambda = 0.5; % 半波长间距
steering_vectors = exp(1i*2*pi*d_lambda*(0:numRX-1)'*sin(theta_rad)); % [numRX x Ntheta]
A = steering_vectors;
Ntheta = length(theta);
V = size(MIX, 2); % 快拍数

%% 邻接矩阵 (线形拓扑)
adj = spdiags(ones(V-1,2), [-1,1], V, V); % 稀疏矩阵存储

%% 初始化变量 (预分配内存)
x = cell(V,1);
s_prev = cell(V,1);
c = cell(V,1);
for v = 1:V
    x{v} = A' * MIX(:,v); % 初始估计 [Ntheta x 1]
    s_prev{v} = true(Ntheta,1); % 激活状态逻辑矩阵
    c{v} = zeros(Ntheta,1); % 计数器
end
stop_flags = false(V,1);

%% 主循环 (向量化核心计算)
for iter = 1:params.MaxIter
    s_current = cell(V,1);
    any_updated = false;
    
   for v = 1:V % 启用并行计算
        if stop_flags(v), continue; end
        
        % 当前节点数据
        xv_old = x{v};
        yv = MIX(:,v);
        
        % 梯度更新
        residual = yv - A*xv_old;
        zv = xv_old + params.Tau*(A'*residual);
        
        % 邻居激活状态
        neighbors = find(adj(v,:));
        if isempty(neighbors)
            avg_s = 0;
        else
            avg_s = mean(cell2mat(cellfun(@(s) double(s), s_prev(neighbors), 'UniformOutput', false)), 2);
        end
        
        % 自适应阈值 (向量化计算)
        w = max(params.Beta - params.Alpha*abs(xv_old) - avg_s, 0);
        
        % 软阈值收缩
        xv_new = sign(zv) .* max(abs(zv) - params.Lambda*w, 0);
        
        % 强制置零条件
        zero_mask = (xv_old ~= 0) & (c{v} >= params.P);
        xv_new(zero_mask) = 0;
        
        % 更新计数器
        update_c = (xv_old ~= 0) & (xv_new ~= 0);
        c{v} = c{v} + update_c;
        
        % 收敛判断
        delta = norm(xv_new - xv_old);
        if delta < params.Epsilon
            stop_flags(v) = true;
        else
            x{v} = xv_new;
            s_current{v} = xv_new ~= 0;
            any_updated = true;
        end
    end
    
    % 更新激活状态
    s_prev = s_current;
    
    % 提前终止
    if ~any_updated, break; end
end

%% 结果合成 (多节点融合)
x_est = mean(cell2mat(x'), 2); % 取节点平均
Power_Ssv = abs(x_est).^2;

%% 性能统计
fprintf('算法收敛于 %d 次迭代\n', iter);
end