ICLR2020 | SGM | 跳跃连接很重要：关于用 ResNets 生成的对抗样本的迁移能力

---

论文链接

本文 “Skip Connections Matter: On the Transfer Ability of Adversarial Examples Generated with ResNets” 主要研究了深度神经网络（DNN）中跳连接（skip connections）在对抗样本生成与迁移方面的特性，发现跳连接会使网络更易生成高迁移性的对抗样本，并提出 Skip Gradient Method（SGM）利用这一特性提升攻击效果，对 DNN 安全研究有重要意义。

---

摘要-Abstract

Skip connections are an essential component of current state-of-the-art deep neural networks (DNNs) such as ResNet, WideResNet, DenseNet, and ResNeXt. Despite their huge success in building deeper and more powerful DNNs, we identify a surprising security weakness of skip connections in this paper. Use of skip connections allows easier generation of highly transferable adversarial examples. Specifically, in ResNet-like (with skip connections) neural networks, gradients can backpropagate through either skip connections or residual modules. We find that using more gradients from the skip connections rather than the residual modules according to a decay factor, allows one to craft adversarial examples with high transferability. Our method is termed Skip Gradient Method (SGM). We conduct comprehensive transfer attacks against state-of-the-art DNNs including ResNets, DenseNets, Inceptions, Inception-ResNet, Squeeze-and-Excitation Network (SENet) and robustly trained DNNs. We show that employing SGM on the gradient flow can greatly improve the transferability of crafted attacks in almost all cases. Furthermore, SGM can be easily combined with existing black-box attack techniques, and obtain high improvements over state-of-the-art transferability methods. Our findings not only motivate new research into the architectural vulnerability of DNNs, but also open up further challenges for the design of secure DNN architectures.

跳跃连接是当前最先进的深度神经网络（DNN）如 ResNet、WideResNet、DenseNet 和 ResNeXt 的重要组成部分。尽管它们在构建更深层、更强大的 DNN 方面取得了巨大成功，但在本文中我们发现了跳跃连接一个令人惊讶的安全弱点。使用跳跃连接使得更容易生成具有高迁移性的对抗样本。具体来说，在类似 ResNet（有跳跃连接）的神经网络中，梯度可以通过跳跃连接或残差模块进行反向传播。我们发现，通过一个衰减因子使用更多来自跳跃连接而非残差模块的梯度，能够生成具有高迁移性的对抗样本。我们的方法被称为跳跃梯度法（SGM）。 我们对包括 ResNets、DenseNets、Inceptions、Inception-ResNet、挤压与激励网络（SENet）以及经过鲁棒训练的 DNN 等最先进的 DNN 进行了全面的迁移攻击。我们表明在梯度流上采用 SGM 几乎在所有情况下都能极大地提高所生成攻击的迁移性。此外，SGM 可以很容易地与现有的黑盒攻击技术相结合，并在最先进的迁移性方法上取得很大的改进。我们的发现不仅激发了对 DNN 架构漏洞的新研究，也为安全 DNN 架构的设计带来了进一步的挑战。

---

引言-Introduction

该部分主要阐述了深度神经网络中跳连接的重要性以及其在对抗样本攻击方面存在的安全隐患，还介绍了相关研究背景与本文的主要贡献，具体内容如下：

• 跳连接的重要性与 DNN 的安全问题
  • 在深度神经网络中，跳连接通过直接连接卷积块（残差模块）的输入和输出，构建了从浅层到深层的捷径。它有助于保留低级特征，避免在增加网络层数时出现性能下降，对构建如 ResNet、WideResNet、DenseNet 和 ResNeXt 等强大的深度神经网络至关重要。
  • 尽管深度神经网络性能优异，但极易受到对抗样本（攻击）的影响。对抗样本是对输入示例进行微小扰动以欺骗网络做出错误预测的样本，它们通常对人类观察者来说难以察觉，且能在不同模型间迁移，这在人脸识别、自动驾驶、视频分析和医疗诊断等安全关键场景的 DNN 部署中引发了安全担忧。
• 对抗样本攻击方法的局限性与研究空白
  • 对抗样本可在白盒（攻击者完全了解目标模型）或黑盒（攻击者对目标模型无信息）设置下生成。白盒方法如 FGSM、BIM、PGD 和 CW 等在黑盒设置下迁移性低，对实际中通常保密的 DNN 模型威胁有限。
  • 已有一些技术如动量提升、多样输入和平移不变性等来提高基于代理模型生成的黑盒攻击的迁移性，但这些技术以及白盒方法都将整个网络视为单一组件，忽略了其内部架构特征。关于 DNN 架构本身是否会暴露更多对抗攻击的迁移性这一问题尚未被探索。
• 本文的研究动机与主要贡献
  • 通过对 ResNet - 18 的 BIM 攻击实验发现，使用跳连接的梯度比残差模块的梯度攻击成功率更高且更具迁移性，例如攻击跳过最后两个残差模块时，黑盒成功率从 52.52%提升到 62.10%。
  • 基于此提出 Skip Gradient Method（SGM），通过衰减因子利用更多来自跳连接的梯度生成对抗样本，这是一种简单通用的技术，可应用于任何基于梯度的攻击方法。
  • 进行了全面的迁移攻击实验，结果表明 SGM 能大幅提高对抗样本的迁移性，与现有迁移技术结合可显著提升当前的迁移性基准，为 DNN 架构漏洞研究和安全架构设计带来新的思考与挑战。

图 1：左：在 ImageNet 上训练的 ResNet - 18 的最后 3 个跳跃连接（绿色线条）和残差模块（黑色方框）的图示。右：在每个连接点（圆圈）处，使用通过跳跃连接（向上）或残差模块（向左）的梯度制作的对抗攻击的成功率（以“白盒/黑盒”的形式）。用不同颜色突出显示了三个示例反向传播路径，其中跳过最后两个残差模块的绿色路径具有最高的攻击成功率，而穿过所有 3 个残差模块的红色路径具有最低的攻击成功率。这些攻击是通过 BIM 在 5000 张 ImageNet 验证图像上制作的，最大 $L_{\infty }$ 扰动 $ϵ=16$（像素值在 [0, 255] 范围内）。黑盒成功率是针对 VGG19 目标模型进行测试的。

---

相关工作-Related Work

相关工作部分主要介绍了现有对抗攻击的分类及各类别下的具体方法，具体内容如下：

• 白盒攻击
  • Fast Gradient Sign Method (FGSM)：通过沿梯度方向对清洁示例 $x$ 进行一步扰动，扰动量为 $ϵ$，公式为 $x_{adv}=x+ϵ\cdot sign({\nabla }_x\ell (f(x),y))$。
  • Basic Iterative Method (BIM)：FGSM的迭代版本，进行 $T$ 步扰动，步长为 $\Vert T\Vert$。
  • Projected Gradient Descent (PGD)：对正常示例 $x$ 进行 $T$ 步较小步长的扰动，每次扰动后若超出 $ϵ$ - 球则投影回，公式为 $x_{adv}^{t+1}={\Pi }_{ϵ}(x_{adv}^t+\alpha \cdot sign({\nabla }_x\ell (f(x_{adv}^t),y)))$，允许步长 $\alpha >ϵ/T$。
  • 还有其他基于稀疏性的方法如Jacobian - based Saliency Map Attack (JSMA)、sparse attack、one - pixel attack，以及基于优化的方法如Carlini and Wagner (CW)和elastic - net (EAD)等。
• 黑盒攻击
  • 可通过攻击代理模型或使用梯度估计方法结合对目标模型的查询来生成。梯度估计方法如Finite Differences (FD)或Natural Evolution Strategies (NES)，但需要大量查询目标模型，效率低且易暴露攻击。
  • 也可在代理模型上制作对抗样本再攻击目标模型。针对白盒方法在黑盒设置下效果不佳的问题，已有多种提升迁移性的技术：
    • Momentum Iterative boosting (MI)：将动量项纳入梯度以提升迁移性，公式为 $x_{adv}^{t+1}={\Pi }_{ϵ}(x_{adv}^t+\alpha \cdot sign(g^{t+1})),g^{t+1}=\mu \cdot g^t+\frac{{\nabla }_x\ell (f(x_{adv}^t),y)}{\Vert {\nabla }_x\ell (f(x_{adv}^t),y){\Vert }_1}$。
    • Diverse Input (DI)：使用关于随机变换输入示例的梯度制作对抗样本，公式为 $x_{adv}^{t+1}={\Pi }_{ϵ}(x_{adv}^t+\alpha \cdot sign({\nabla }_x\ell (f(H(x_{adv}^t;p)),y)))$。
    • Translation Invariant (TI)：通过生成对代理模型判别区域不太敏感的对抗样本来规避鲁棒训练的 DNNs，公式为 $x_{adv}^{t+1}={\Pi }_{ϵ}(x_{adv}^t+\alpha \cdot sign(W\ast {\nabla }_x\ell (f(x_{adv}^t),y)))$。
  • 还有其他关注中间特征表示的研究，如Activation Attack和Intermediate Level Attack，但现有转移技术包括白盒攻击都未直接考虑不同 DNN 架构特征的影响。

---

提出的跳跃梯度攻击-Proposed Skip Gradient Attack

该部分主要围绕提出的 Skip Gradient Attack 展开，包括跳连接的梯度分解、Skip Gradient Method（SGM）的介绍以及通过案例研究展示跳连接在对抗迁移性方面的特性，具体内容如下：

• 梯度分解与跳连接
  • 在类似 ResNet 的神经网络中，跳连接利用恒等映射绕过残差层，使数据能从浅层直接流向深层，可将网络分解为不同长度的路径集合。以包含三个连续构建块（如 $z_{i+1}=z_i+f_{i+1}(z_i)$）的残差网络为例，从输入 $z_0$ 到输出 $z_3$，根据链式法则，损失函数 $\ell$ 关于输入 $z_0$ 的梯度可分解为 $\frac{\partial \ell }{\partial z_0}=\frac{\partial \ell }{\partial z_3}(1+\frac{\partial f_3}{\partial z_2})(1+\frac{\partial f_2}{\partial z_1})(1+\frac{\partial f_1}{\partial z_0})$，并可推广到具有 $L$ 个残差块的网络。
• Skip Gradient Method（SGM）
  • 为更多地利用跳连接的梯度，引入衰减参数 $\gamma$ 到分解梯度中，以减少残差模块的梯度。对于具有 $L$ 个残差块的网络，“跳过”的梯度为 ${\nabla }_x\ell =\frac{\partial \ell }{\partial z_L}{\prod }_{i=0}^{L-1}(\gamma \frac{\partial f_{i+1}}{\partial z_i}+1)\frac{\partial z_0}{\partial x}$，其中 $z_0=x$ 为网络输入，$\gamma \in (0,1]$。给定干净样本 $x$ 和 DNN 模型 $f$，可迭代生成对抗样本 $x_{adv}^{t+1}={\Pi }_{ϵ}(x_{adv}^t+\alpha \cdot sign(\frac{\partial \ell }{\partial z_L}{\prod }_{i=0}^{L-1}(\gamma \frac{\partial f_{i+1}}{\partial z_i}+1)\frac{\partial z_0}{\partial x}))$。SGM 可在任何有跳连接的神经网络上轻松实现，在反向传播过程中，每当梯度经过残差模块时乘以衰减参数，无需额外计算开销，且在密集连接网络如 DenseNets 上也能高效工作，其对残差梯度的减少沿反向传播路径累积。
• 跳连接的对抗迁移性：案例研究
  • 对 10 步 PGD 及其 SGM 版本进行案例研究，以探究操纵跳连接与否对黑盒攻击成功率（迁移性）的影响。在 8 个不同源（代理）模型（ResNet(RN)-18/34/50/101/152 和 DenseNet(DN)121/169/201）上生成黑盒攻击，并应用于攻击 Inception V3 目标模型，所有模型在 ImageNet 训练集上训练。随机选取 5000 张被所有源模型正确分类的 ImageNet 验证图像，在最大 $L_{\infty }$ 扰动 $ϵ=16$ 下制作无目标攻击。PGD 步长设为 $\alpha =2$，SGM 衰减参数设为 $\gamma =0.5$，每种攻击运行 5 次并报告成功率。
  • 结果显示，使用 SGM 操纵跳连接后，PGD 的迁移性在所有源模型上都有大幅提高，除 RN18 外，在其他源模型上的提升均超 13%。未使用 SGM 时，针对 Inception-V3 目标模型的最佳迁移性为 35.48%（由 PGD 在 DN201 上实现），而使用 SGM 后提升到 65.38%。同时发现，在同一 ResNet 家族内网络跳连接越多，或从 ResNets 到 DenseNets，所生成的对抗样本迁移性越强，这引发了对现有 DNN 设计原则（如利用跳连接和 1×1 卷积“加深”网络）的思考。

表 1：由 PGD 及其“跳跃梯度”（SGM）版本生成的无目标黑盒攻击在不同源模型上针对 Inception V3 目标模型的成功率（5 次随机运行的百分比±标准差）。最佳结果以粗体显示。

---

与现有迁移攻击的比较-Comparison To Existing Transfer Attacks

该部分主要比较了所提出的 SGM 与现有方法在生成对抗样本迁移性方面的表现，包括针对非安全模型和鲁棒训练模型的研究，以及对 SGM 的进一步探究，具体内容如下：

• 实验设置

  • 基线方法：将 SGM 与 FGSM、PGD 以及 3 种先进的迁移攻击方法（MI、DI、TI）进行比较，对 TI 和 SGM 测试一步和迭代版本，其他方法仅测试迭代版本，迭代步数根据目标模型安全性设置，步长等参数按各自原始论文配置，在实验中用 SGM 表示一步攻击中的 FGSM + SGM 和多步攻击中的 PGD + SGM。
  • 威胁模型：采用黑盒威胁模型，在 5000 张被源模型正确分类的 ImageNet 验证图像上生成对抗样本攻击目标模型，重复 5 次，攻击为在最大 $L_{\infty }$ 扰动 $ϵ=16$ 下的无目标攻击。
  • 目标模型：包括在 ImageNet 训练集上传统训练的 7 种非安全模型（如 VGG19、ResNet - 152 等）和 3 种通过对抗训练得到的安全模型（如 $IncV{3}_{ens3}$ 等）。
  • 源模型：从 ResNet 家族中选择 8 种不同模型（ResNet(RN)18/34/50/101/152 和 DenseNet(DN)-121/169/201），根据目标模型调整对抗图像尺寸。

• 针对非安全模型的迁移性

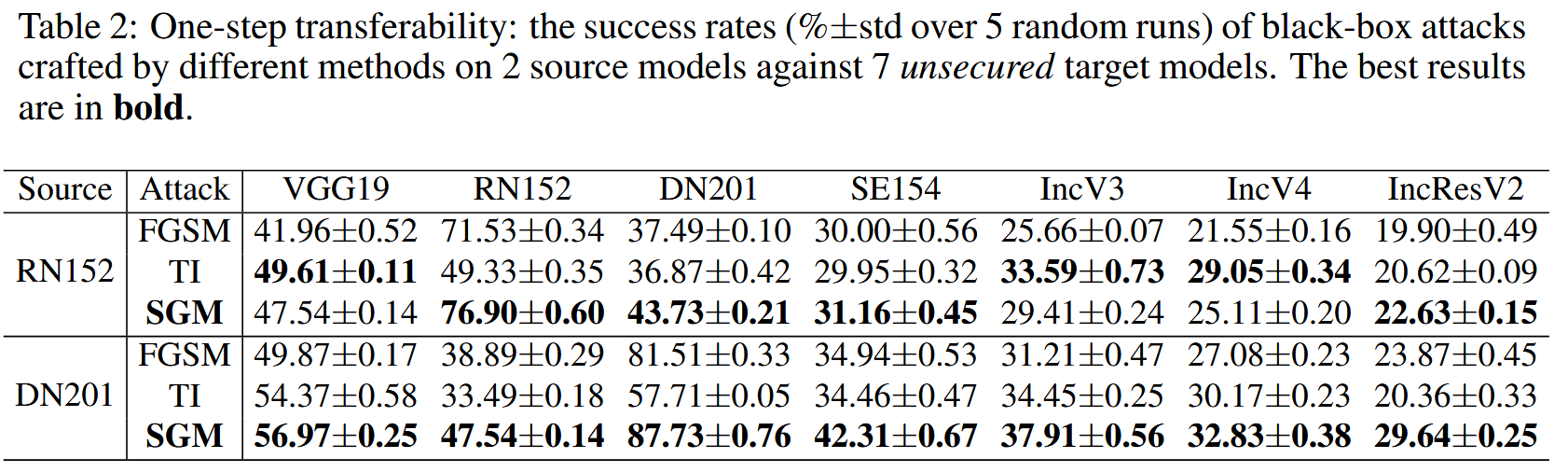
  • 一步迁移性：在 RN152 和 DN201 两个源模型上测试，结果表明在 DN201 上生成的对抗样本迁移性更好，SGM 在多数情况下优于 FGSM 和 TI，但从 RN152 转移到部分模型时 TI 表现更好，说明跨架构时平移适应可提升一步扰动的迁移性，且在跳连接多的源模型（如 DN201）中 SGM 优势更显著。
    表 2：一步迁移性：不同方法在 2 个源模型上针对 7 个非安全目标模型制作的黑盒攻击的成功率（5 次随机运行的%±标准差）。最佳结果以粗体显示。
    
  • 多步迁移性：对 8 个源模型攻击 3 个代表性非安全目标模型（VGG19、SE154、IncV3），SGM 在多数源模型上优于现有方法，且源模型跳连接越多，SGM 攻击迁移性越强；同时发现目标模型深度影响源模型迁移性，浅目标模型适合浅源模型攻击，深目标模型适合深源模型攻击。在最佳源模型 RN152 和 DN201 上，SGM 相比其他方法优势明显，如在 DN201 到 SE154 的攻击中，SGM 成功率比 MI 和 DI 分别高 7%和 10%以上。
    
    图 2：不同攻击方法在 8 个源模型上针对 3 个非安全目标模型（VGG19（左）、SE154（中）和 IncV3（右））生成的黑盒攻击的攻击成功率。
    表 3：多步迁移性：不同方法在两个源模型上针对 7 个非安全目标模型制作的黑盒攻击的成功率（5 次随机运行的%±标准差）。最佳结果以粗体显示。
    
  • 与现有方法结合：在 DN201 上实验，结果显示 SGM 可显著提升 MI 和 DI 的迁移性，与两者结合后大幅提高了当前最佳（MI + DI）的迁移性，如将新的最佳迁移性提升到至少 80.52%（之前为 71%）。
    表 4：与现有方法结合：在源模型 DN201 上制作的针对 7 个非安全目标模型的攻击成功率（%）。最佳结果以粗体显示，“+”表示改进。
    

• 针对鲁棒训练模型的迁移性

  • TI 在攻击安全模型时单独迁移性最佳，SGM 次之，但 SGM 与 TI 结合能大幅提升 TI 攻击效果，表明操纵跳连接虽不足以单独攻击安全模型，但可增强现有攻击能力。与攻击非安全模型相反，在 RN152 上生成的对抗样本比 DN201 更具迁移性。
    表 5：针对安全模型的迁移性：在 RN152 和 DN201 源模型上制作的针对 3 个安全模型的多步攻击的成功率（5 次随机运行的%±标准差）。最佳结果以粗体显示。
    

• 对 SGM 的进一步探究

  • 残差梯度衰减 $\gamma$ 的影响：测试不同 $\gamma \in [0.1,1.0]$ 下 SGM 的迁移性，结果显示在 DenseNet 源模型上，$\gamma$ 小于一定阈值（如 0.5）时降低 $\gamma$ 可提升迁移性；在 ResNet 源模型上，$\gamma \ge 0.2$ 时降低 $\gamma$ 可提升迁移性，且 $\gamma$ 的选择主要取决于源模型，在不知目标模型时，可在源模型上调参找到最佳 $\gamma$。
    
    图 3：参数调整：通过 10 步 SGM 生成的黑盒攻击的成功率，其衰减参数 $\gamma$ 在 [0.1, 1.0] 范围内变化。实线和虚线曲线分别代表在 ResNet 和 DenseNet 源模型上的结果。
  • 集成攻击：基于 RN34、RN152 和 DN201 进行集成攻击，根据源模型选择最佳 $\gamma$。结果显示，针对非安全目标模型，SGM 单独性能与 DI 相似且优于其他方法，结合其他方法后可大幅提高成功率；针对安全目标模型，SGM 单独迁移性排第二，与 TI 结合后可提升约 10%的成功率。
    表 6：基于集成的攻击的多步迁移性：不同方法在由 3 个源模型（例如 RN34、RN152 和 DN201）组成的集成上针对 7 个非安全目标模型制作的多步攻击的成功率（5 次随机运行的%±标准差）。最佳结果以粗体显示。
    
    表 7：基于集成的攻击对安全模型的迁移性：在由 3 个源模型（例如 RN34、RN152 和 DN201）组成的集成上制作的黑盒攻击的成功率（5 次随机运行的%±标准差）。最佳结果以粗体显示。
    
  • 改进弱白盒攻击：SGM 可提升弱白盒攻击 FGSM 的效果，在最大 $L_{\infty }$ 扰动 $ϵ\ge 4$ 时优势明显，因为复杂模型一步梯度可靠性低，跳梯度更可靠，且随着模型复杂度增加，对抗强度会降低。
    
    图 4：FGSM 与 SGM 的白盒成功率。在（b）和（c）中，每种颜色对应一个模型，其中 FGSM 由实线表示，SGM 由虚线表示。

---

结论-Conclusion

该部分主要强调了研究发现的重要性以及对后续研究和 DNN 架构设计的影响，具体内容如下：

• 发现许多先进的类似 ResNet 的神经网络中的跳连接具有易生成高迁移性对抗样本的特性，这一特性此前未被充分认识。
• 为证明此架构“弱点”提出的 Skip Gradient Method（SGM），通过衰减因子利用跳连接的梯度来生成对抗样本，在一系列包含 8 个源模型和 10 个目标模型（其中 7 个非安全模型和 3 个安全模型）的迁移攻击实验中，SGM 生成的攻击相比现有方法具有显著更好的迁移性，且与现有技术结合能极大提升当前的迁移性基准。
• 认为跳连接的高对抗迁移性源于其暴露了额外的低层级信息，这些信息在不同 DNN 间更易迁移。
• 研究结果提醒对抗研究领域的研究者关注 DNN 架构的脆弱性，同时也给安全 DNN 架构设计带来了新的挑战，为后续相关研究指明了方向。