AAAI2025 | MuMoDIG | 通过改进积分路径提高基于积分梯度的对抗样本迁移性_improving integrated gradient-based transferable-CSDN博客

本文链接：https://blog.csdn.net/qq_60090693/article/details/146212315

Improving Integrated Gradient-based Transferable Adversarial Examples by Refining the Integration Path

摘要-Abstract
引言-Introduction
相关工作-Related Work
方法-Methodology
实验-Experiments
结论与展望-Conclusion and Outlook

本文 “Improving Integrated Gradient - based Transferable Adversarial Examples by Refining the Integration Path” 提出 MuMoDIG 攻击方法，从多路径、单调性和多样性三方面优化积分路径，生成高迁移性对抗样本，在多种模型和防御机制下表现优异。

摘要-Abstract

Transferable adversarial examples are known to cause threats in practical, black-box attack scenarios. A notable approach to improving transferability is using integrated gradients (IG), originally developed for model interpretability. In this paper, we find that existing IG-based attacks have limited transferability due to their naive adoption of IG in model interpretability. To address this limitation, we focus on the IG integration path and refine it in three aspects: multiplicity, monotonicity, and diversity, supported by theoretical analyses. We propose the Multiple Monotonic Diversified Integrated Gradients (MuMoDIG) attack, which can generate highly transferable adversarial examples on different CNN and ViT models and defenses. Experiments validate that MuMoDIG outperforms the latest IG-based attack by up to 37.3% and other state-of-the-art attacks by 8.4%. In general, our study reveals that migrating established techniques to improve transferability may require non-trivial efforts.

可迁移对抗样本在实际的黑盒攻击场景中会造成威胁。一种显著的提高可迁移性的方法是使用积分梯度（IG），该方法最初是为模型可解释性而开发的。在本文中，我们发现现有的基于IG的攻击由于在模型可解释性中对IG的简单采用，其可转移性有限。为了解决这一限制，我们聚焦于IG积分路径，并从三个方面对其进行优化：多重性、单调性和多样性，且有理论分析作为支撑。我们提出了多重单调多样化积分梯度（MuMoDIG）攻击方法，它可以在不同的卷积神经网络（CNN）和视觉Transformer（ViT）模型以及防御机制上生成具有高可迁移性的对抗样本。实验验证，MuMoDIG比最新的基于IG的攻击性能高出37.3%，比其他最先进的攻击高出8.4%。总体而言，我们的研究表明，迁移已有的技术来提高可转移性可能需要付出相当大的努力。

引言-Introduction

该部分主要介绍了研究背景、现有问题、解决方法和主要贡献，具体内容如下：

研究背景：深度学习网络（DNNs）易受对抗攻击，其中黑盒攻击因缺乏模型细节更具挑战性，可迁移黑盒攻击则依赖在已知代理模型上生成的对抗样本的可迁移性。为评估和提高DNN模型在实际场景中的鲁棒性，人们提出了多种可迁移攻击方法。近期，一些可迁移攻击将积分梯度（IG）从模型可解释性任务迁移过来，利用IG的累积效应增强对抗梯度的稳定更新方向，提升可转移性。
现有问题：现有基于IG的攻击直接采用单路径的IG实现方式，这种简单的应用使得计算出的梯度易受输出流形高曲率位置的影响，从而在很大程度上限制了攻击的可迁移性。
解决方法：为解决上述问题，文章从三个关键方面对IG的积分路径进行优化。在多重性方面，提出多重积分梯度（MuIG），让基线b服从某种分布而非固定为黑色图像；在单调性方面，定义单调积分路径并证明其在生成对抗样本中的重要性，同时提出下边界量化（LBQ）方法生成符合要求的基线；在多样性方面，通过复合随机变换对路径进行多样化处理，以降低路径上插值点的余弦相似度，避免过拟合。最终提出了多重单调多样化积分梯度（MuMoDIG）攻击方法。
主要贡献：一是指出现有基于IG的攻击因单路径IG的简单采用导致可转移性受限，并从三个关键方面优化积分路径；二是提出MuMoDIG攻击方法，并进行全面分析支撑其设计；三是通过在ImageNet上针对多种CNN和ViT模型及流行防御机制的大量实验，验证了MuMoDIG的优越性，其性能比最新的基于IG的攻击高出37.3%，比其他先进攻击高出8.4%.

在这里插入图片描述
图1：由我们的MuMoDIG和MIG（Ma等人，2023年）在目标模型PiT-T上生成的对抗样本的模型归因结果对比。MuMoDIG更聚焦于图像背景，这展示了它在干扰模型预测方面的优势。此处，RN-18为代理模型。

方法-Methodology

迁移攻击中的积分梯度-Integrated Gradients in Transferable Attacks

该部分介绍了可迁移攻击中积分梯度的应用及本文改进的思路与方法，具体内容如下：

可迁移攻击的优化目标：可转移攻击旨在对代理模型上的干净图像 $x$ 优化一个受 $\epsilon$ 约束的对抗扰动 $\delta'$ ，通过公式 $\delta'=\underset{\delta}{arg max } L(f(x+\delta), y), s.t. \| \delta\| _{\infty} \leq \epsilon$ 来实现，其中 $f (x)$ 是softmax输出， $L$ 通常是交叉熵损失函数， $\epsilon$ 常用 $L_{p}$ 范数衡量，也会探索其他感知度量。
积分梯度计算：积分梯度（IG）是与输入图像维度相同的张量，在生成对抗扰动时，其第 $i$ 个元素的计算式为 $G\left(x_{t}\right)_{i}=\left(\left(x_{t}\right)_{i}-b_{i}\right) \cdot \int_{0}^{1} \frac{\partial f\left(b+\alpha \cdot\left(x_{t}-b\right)\right)}{\partial\left(x_{t}\right)_{i}} d \alpha$ ，通常使用近似公式 $G\left(x_{t}\right)_{i} \approx \frac{\left(\left(x_{t}\right)_{i}-b_{i}\right)}{N_{I}} \cdot \sum_{k=0}^{N_{I}-1} \frac{\partial f\left(b+\frac{k+\lambda}{N_{I}} \cdot\left(x_{t}-b\right)\right)}{\partial\left(x_{t}\right)_{i}}$ ，其中 $x_{t}=x+\delta_{t}$ 是第 $t$ 次迭代的输入图像，基线 $b$ 一般为黑色图像， $N_{I}$ 是插值点数量， $\lambda \in[0,1]$ 控制插值点位置。

在这里插入图片描述
图2：（a）MIG（Ma等人，2023年）采用以黑色图像为基线的单条积分路径。（b）我们的MuIG采用具有任意基线的多条积分路径，（c）MuMoIG进一步强化了单调性，（d）MuMoDIG $_{all}$ 使路径多样化并保留所有路径，不强制其单调性，（e）MuMoDIG去除非单调的多样化路径。

使用多重单调积分路径进行攻击-Attack with Multiple Monotonic Integration Paths

该部分内容指出单路径IG在可迁移攻击中存在局限性，提出了多重单调积分路径的攻击方法，具体如下：

单路径IG的局限性：基于模型可解释性的现有研究表明，单路径的IG会因输出流形的高曲率位置积累不稳定梯度。在可迁移攻击中直接使用IG时，这一问题同样存在，会限制攻击效果。

图3：输出流形的高曲率位置对单条积分路径的影响。
多重积分梯度（MuIG）：为解决单路径IG的问题，提出MuIG. 与以往固定黑色图像作为基线不同，MuIG假设基线b服从某种分布，通过对公式添加期望操作 $E_{b}$ ，计算第 $i$ 个元素 $MuIG(x_{t})_{i}=E_{b}(IG(x_{t})_{i})$ . 然而，探索性实验发现，使用任意基线会随着基线数量增加损害迁移性。因为积分路径 $x_{t}-b)$ 的符号不一定与梯度 $\frac{\partial f(x_{t}+\alpha \cdot(x_{t}-b))}{\partial x_{t}}$ 的符号一致，当两者元素符号完全相反时，会严重破坏梯度方向，导致更新方向相反，降低迁移性。
单调积分路径：为避免积分路径与梯度之间的冲突，定义了单调积分路径。对于由一系列插值点 $x_{0},...,x_{N_{I}-1})$ 组成的积分路径，若对于任意插值点 $x_{k}$ ，满足 $\forall s<k$ ， $(x_{s})_{i} \leq(x_{k})_{i}$ 且 $\forall m>k$ ， $(x_{m})_{i} \geq(x_{k})_{i}$ （其中 $0 ≤s<k<m ≤N_{I}-1$ 且 $\cdot H \cdot W$ ），则该路径为单调积分路径。同时给出命题，在使用积分梯度生成可迁移攻击的对抗样本时，积分路径应是单调积分路径。该定义保证了序列中前面插值点的元素始终小于或等于后面插值点的对应元素，使对抗样本生成过程中梯度元素的符号不会被积分路径改变，解释了现有方法（如MIG）使用黑色图像基线能增强转移性的原因，因为其天然形成了单调积分路径。
下边界量化（LBQ）方法：受随机量化方法启发，提出LBQ方法来生成符合单调积分路径要求的基线。具体步骤为：先将 $x_{t}$ 的每个通道转换为一维向量并按值升序排序；然后随机选择 $N_{R}-1(2 ≤N_{R})$ 个划分将向量分割成 $N_{R}$ 个区域，把每个区域的元素替换为该区域的最小值；最后将处理后的向量转换回每个通道的原始维度。使用LBQ方法生成基线的MuIG被称为多重单调积分梯度（MuMoIG）。

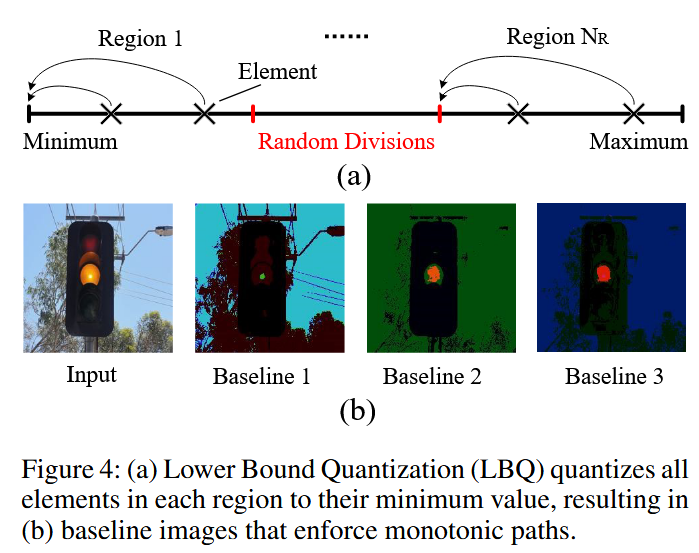
图4：(a)下边界量化（LBQ）将每个区域中的所有元素量化为其最小值，从而生成(b)强制执行单调路径的基线图像。

利用多样积分路径进行攻击-Attack with Diversified Integration Paths

该部分主要介绍了在确保积分路径单调性的基础上，如何通过多样化积分路径进一步提升攻击效果，具体内容如下：

梯度相似性问题：在保证多重积分路径单调性后，研究发现沿路径的插值点梯度缺乏多样性。计算插值点梯度的余弦相似度发现，相邻位置梯度的余弦相似度很高。使用这样相似的梯度进行累加，无法有效减少对代理模型的过拟合，因为这些梯度在高维空间中提供的信息有限。

图5：沿直线路径上10个插值点处梯度之间计算出的余弦相似度。
多样化积分路径的实现：为解决上述问题，文章借鉴前人工作，通过应用输入变换来降低梯度的余弦相似度。具体通过公式 $MuMoDIG_{all}(x_{t})_{i}=E_{T}(E_{b | T}(IG_{all}(x_{t})_{i}))$ 来实现，其中 $T$ 表示输入变换。为确保足够的梯度多样性，变换通常包含复合操作，每次随机选择一种操作。这里采用了调整大小和填充（RP）以及仿射变换（AF）这两种简单变换，且选择概率相等。这样得到了 Multiple Monotonic Diversified Integrated Gradients $_{all}$ （MuMoDIG $_{all}$ ），保留所有多样化路径，无论其是否满足单调性。
3. 去除非单调路径：由于变换后的输入到原输入的积分路径不能保证单调，违反了之前提出的单调积分路径命题。因此，需要丢弃这些非单调路径，公式变为 $MuMoDIG(x_{t})_{i}=E_{T}(E_{b | T}(IG_{mo}(x_{t})_{i}))$ ，并可通过蒙特卡罗采样近似为 $MuMoDIG(x_{t})_{i} \approx I \cdot \sum_{p=0}^{N_{T}} \sum_{q=0}^{N_{B}-1}(IG_{mo}(x_{t})_{p,q})_{i}$ ，其中 $I=\frac{1}{(N_{T}+1) \cdot N_{B}}$ ， $N_{T}$ 为采样变换的数量， $N_{B}$ 为采样基线的数量。在进行所有这些步骤后，最终得到了多重单调多样化积分梯度（MuMoDIG）攻击方法。
其他优化措施：与MIG类似，MuMoDIG也结合了动量项来进一步提升转移性。同时发现，使用 $l o g f (x)$ 而不是 $- f (x)$ 作为损失函数，对本文方法和现有基于IG的攻击都能带来稍好的性能表现。

IG对于解释性和迁移性的比较-IG for Interpretability vs. for Transferabability

该部分主要阐述了积分梯度（IG）在模型可解释性和可转移性攻击这两个应用场景中的差异，以及直接将先进IG技术用于可迁移性攻击存在的问题。具体内容如下：

应用目标差异：IG在模型可解释性中，重点在于通过突出梯度与积分路径乘积的整体大小，为模型预测提供更好的视觉解释，使人们能直观理解模型决策依据。而在迁移攻击场景下，目标是干扰模型的预测结果，此时梯度方向的符号比乘积大小更为关键，因为它直接决定了对抗样本的生成方向，影响能否成功误导模型。
先进IG技术用于可转移性攻击的问题
- BlurIG的问题：BlurIG采用一系列模糊图像作为基线来计算IG。这与MuIG中随意选择多个基线的情况类似，无法形成单调积分路径。在可迁移性攻击中，非单调的积分路径会导致梯度方向不稳定，影响对抗样本的生成质量，进而限制攻击的转移性。
- GIG和IDGI的问题：GIG和IDGI虽然都以黑色图像作为基线，从起点到终点的直线能形成单调积分路径，但在实际计算过程中，中间的积分路径无法保证单调性。这就如同MuMoDIG $_{all}$ 存在的问题一样，非单调路径会干扰梯度计算，使得生成的对抗样本难以有效迁移到目标模型，降低了攻击效果。

实验-Experiments

实验设置-Experimental Setup

该部分详细介绍了实验所涉及的数据集、攻击基线、实验参数、模型以及防御机制等设置，具体内容如下：

数据集和攻击基线：实验采用ILSVRC2012验证集中的1000张图像。将MuMoDIG与最新的基于IG的攻击方法MIG，以及具有复合操作的先进可转移攻击方法（如SSA、GRA和SIA）进行比较。这些对比方法都基于至少一种变换，配备了多种输入变换或特殊的梯度修改策略。此外，文中还指出Path - Augmented Method（PAM）和Neuron Attribution - based Attack（NAA）虽与路径相关，但并非基于IG的攻击，附录中展示了MuMoDIG相较于它们的优越性。
参数设置：所有攻击方法的最大攻击迭代次数 $K = 10$ ，最大扰动边界 $\epsilon = 16$ ，步长 $\alpha = 1.6$ ，动量衰减因子 $\mu = 1.0$ 。在LBQ方法中，位置因子 $\lambda = 0.65$ ，区域数量 $N_{R}=2$ 。为保证公平比较，所有攻击在每次迭代时的总辅助输入数量 $N = 6$ 。对于MuMoDIG，设置 $N_{T}=6$ ， $N_{B}=1$ ， $N_{I}=1$ ，使得 $N_{T} \cdot N_{B} \cdot N_{I}=6$ 。
模型和防御机制：代理模型包括三种CNN（RN - 18、DN - 121和MN - v3）和三种ViT（PiT - T、Deit - T和Swin - T）；目标模型包含四种CNN（RN - 18、RN - 101、RNX - 50、DN - 121）和四种ViT（ViT - B、PiT - B、Vis - S、Swin - T）。防御机制包括对抗训练（AT）、高级表示引导去噪器（HGD）、神经表示净化器（NRP）、比特深度减少（BDR）和JPEG压缩。此外，还使用MuMoDIG对在线百度云API进行攻击测试。所有实验均在配备8GB显存的RTX 4060 GPU上进行，同时给出了MIG、GRA、SSA、SIA和MuMoDIG生成一张图像（RN - 18）所需的时间，分别为0.21s、0.24s、0.19s、0.20s和0.28s.

攻击结果-Attack Results

该部分主要展示了MuMoDIG与其他攻击方法的对比实验结果，验证了MuMoDIG的有效性和优越性，具体内容如下：

与其他IG - 基于的攻击对比：将MuMoDIG及其中间版本与最新的基于IG的攻击MIG进行比较。结果显示，MuIG性能最差，表明使用任意多个基线会损害转移性。MuMoIG（ $N_{B}=1$ ， $N_{I}=6$ ）和MuMoIG（ $N_{B}=6$ ， $N_{I}=6$ ）比MIG表现更优，突出了多积分路径的有效性。最后，MuMoDIG优于 $MuMoDIG_{all}$ ，证实了从多样化路径中去除非单调路径的合理性。

表1：逐步优化MIG（Ma等人，2023年）以形成我们最终的攻击方法MuMoDIG的攻击成功率（%）。代理模型是RN-18，“平均值”列不包括标有*的白盒攻击结果。
与最先进的基于变换的攻击对比：MuMoDIG在几乎所有情况下都优于其他先进攻击。例如，在MN - v3上生成对抗样本并攻击Swin - T时，MuMoDIG的攻击成功率达到62.4%，比其他攻击中的最佳结果高出10.2%。在攻击具有防御机制的模型时，MuMoDIG在大多数情况下也更胜一筹。此外，通过调整总辅助输入数量 $N$ 的实验表明，MuMoDIG的优越性在不同 $N$ 值下保持一致。

表2：我们的MuMoDIG与最先进的基于变换的攻击方法的攻击成功率（%）对比。对于防御机制，对抗训练（AT）使用RN-50模型，高级表示引导去噪器（HGD）采用其默认设置，神经表示净化器（NRP）、JPEG压缩和比特深度减少（Bit）的结果是在八个目标模型上取平均值。“平均值”列中带下划线的结果为第二好的成绩，且“平均值”列不包括标有*的白盒攻击结果。
MuMoDIG与其他攻击的积分：将MuMoDIG与另外两种典型的可转移攻击（SGM和PNAPO）进行积分，结果表明MuMoDIG可以进一步提升这些攻击的转移性。其中，SGM针对具有残差块的CNN，PNAPO针对ViT。

图6：调整总辅助输入数量N时的平均成功率（%）。代理模型为RN-18，目标模型为其余七个模型。

表3：将MuMoDIG与其他攻击方法相结合后的攻击成功率（%），该结果是在卷积神经网络（CNNs）和视觉Transformer（ViTs）上的平均值。
对真实世界系统的攻击：为测试MuMoDIG的实际有效性，使用其攻击真实世界的视觉系统——百度云API。结果显示，对于所有测试示例，添加扰动后目标系统均做出了错误预测，尽管原始预测具有高置信度。在对100张图像的测试中，MuMoDIG的攻击成功率高达91.0%，而GRA为74.0%，SIA为87.0%。

图7：我们的MuMoDIG对百度云API的攻击示例。RN-18是代理模型。对100张图像的测试结果表明，我们的MuMoDIG达到了91.0%的高攻击成功率（ASR），相比之下，GRA的攻击成功率为74.0%，SIA的攻击成功率为87.0%。

消融研究-Ablation Studies

该部分对MuMoDIG中多个重要参数进行消融研究，分析它们对攻击性能的影响，具体内容如下：

辅助输入数量：总辅助输入数量 $N$ 由插值点数量 $N_{I}$ 、基线数量 $N_{B}$ 和采样变换数量 $N_{T}$ 相乘得到。研究发现，增加这三种辅助输入中任意一种的数量都能提升迁移性。其中，增加 $N_{T}$ 的效果最为显著，因为它能引入更多样化的变换，丰富梯度信息；而增加 $N_{I}$ 的效果最差，这是由于插值点的像素变化不够多样，主要反映像素缩放，更容易导致对代理模型的过拟合。不同辅助输入组合的实验结果进一步证实了这一点。

表4：关于插值点数量 $N_{I}$ 、基线数量 $N_{B}$ 或采样变换数量 $N_{T}$ 的消融研究。结果是在七个目标模型上取平均值。当其中一个数量变化时，其他数量固定为1.

表5：关于采样变换数量 $N_T$ 、基线数量 $N_B$ 和插值点数量 $N_I$ 组合的消融研究，其中 $N_T \cdot N_B \cdot N_I = 6$ .
位置因子：位置因子 $\lambda$ 用于确定直线路径上每个区间内插值点的位置。研究表明，攻击性能对 $\lambda$ 并不敏感，当 $\lambda = 0.65$ 时能取得令人满意的攻击性能。
区域数量：区域数量 $N_{R}$ 是LBQ方法中的关键参数。 $N_{R}$ 较大时，生成的基线接近输入图像； $N_{R}$ 较小时，基线接近黑色图像基线。实验结果显示，随着 $N_{R}$ 增加，迁移性会降低。这是因为较大的 $N_{R}$ 使基线与输入过于接近，导致积分路径缩短，路径上的插值点变得更相似，梯度同质性增加，进而提高了对代理模型的过拟合风险，降低了迁移性。需要注意的是， $N_{R}=1$ 时表示黑色图像基线。

图8：（a）位置因子 $λ$ 和（b）区域数量 $N_{R}$ 的消融研究
输入变换：输入变换 $T$ 也会影响攻击性能。去除现有的变换或用其他常见变换（如模糊或噪声）替代，都会降低迁移性。例如，仅使用仿射变换（AF）或调整大小和填充（RP）时的迁移性不如同时使用两者（即MuMoDIG中的设置），这表明MuMoDIG中采用的复合输入变换对于维持高迁移性至关重要。

表6：输入变换 $T$ 的消融研究

结论与展望-Conclusion and Outlook

该部分总结了研究成果，并对未来研究方向做出展望。该部分指出，研究从多方面优化IG攻击积分路径，提出的MuMoDIG攻击有效，未来可从基线生成等方向深入研究，促进可解释性方法与攻击融合。

研究结论：文章通过在多重性、单调性和多样性三个方面对基于积分梯度（IG）的攻击的积分路径进行优化，提升了其迁移性。具体而言，提出了多重单调多样化积分梯度（MuMoDIG）攻击方法，该方法能够在多种模型和防御机制上生成具有高迁移性的对抗样本。同时，研究通过理论分析揭示了IG在模型解释和可转移攻击应用中的根本差异，为MuMoDIG的设计提供了支撑。实验结果表明，MuMoDIG在攻击成功率上表现出色，优于最新的基于IG的攻击以及其他先进攻击方法。
未来展望：在未来研究中，作者计划从基线生成和探索更合理的积分路径这两个角度，继续推进积分梯度在可转移攻击中的应用研究。此外，还将致力于促进其他可解释性方法与可转移攻击的融合，以期实现更具可解释性的模型评估。