多层前馈网络与误差反传算法
1、多层感知机
1.1 XOR问题
XOR(异或)问题通常指的是一个在机器学习和模式识别中常见的二分类问题。XOR无法进行线性分类,是一种线性不可分问题。

1.2 多层感知机
XOR的解决方法是是使用多层感知机。多层感知机,或者称作多层前馈神经网络,指的是在输入和输出层间加一层或者多层隐单元。三层感知器可识别任一凸多边形或无界的凸区域,更多层感知器网络,可识别更为复杂的图形。三层网络即可解决XOR问题。

多层感知器网络,有如下定理:
定理1:若隐层节点(单元)可任意设置,用三层阈值节点的网络,可以实现任意的二值逻辑函数。
定理2:若隐层节点(单元)可任意设置,用三层S型非线性特性节点的网络,可以一致逼近紧集上的连续函数或按范数逼近紧集上的平方可积函数。
2、BP算法简述
2.1 多层前馈网络
多层感知机是一种多层前馈网络,由多层神经网络构成,每层网络将 输出传递给下一层网络。神经元间的权值连接仅出现在相邻层之间, 不出现在其他位置。如果每一个神经元都连接到上一层的所有神经元 (除输入层外),则成为全连接网络。下面讨论的都是此类网络。

2.2 BP算法简述
多层前馈网络的反向传播 (BP)学习算法,简称BP算法,是有监督的学习,它是梯度下降法在多层前馈网中的应用。BP学习算法由正向传播和反向传播组成:
①正向传播是输入信号从输入层经隐层,传向输出层,若输出层得到了期望的输出,则学习算法结束;否则,转至反向传播。
②反向传播是将误差(样本输出与网络输出之差)按原联接通路反向计算,由梯度下降法调整各层节点的权值和阈值,使误差减小。
3、BP算法详述
3.1 BP算法基本思想
BP算法的基本思想是梯度下降算法,计算过程如下:
①设置初始权系数为较小的随机非零值;
②给定输入/输出样本对,计算网络输出,完成前向传播;
③计算目标函数。如果
,训练成功并退出;否则转入④;
④反向传播计算。由输出层按梯度下降法将误差反向传播,逐层调整权值。
3.2 BP算法推导
假设网络共有L层,其中输入层为第0层,输出层位第L层。记:
①网络中第i层输出:
,其中
为该层的线性输出;
②第i层第j个节点线性输出:
,其中
为连接第i层第j个节点和第i-1层第k个节点的权值;
③网络中第i层线性输出:
,其中
为权矩阵,列数为上层神经元数目,行数为本层神经元数目;
④算法输入输出样本对:
,共N个样本。
3.2.1 前向传播
考虑含一层隐含层的二层神经网络,对于第i层第j个神经元,其输出为:
其中,f可选取LogSigmoid函数。接着需要计算
。
3.2.2 误差反传
①初始化:;
②如果,则
;否则,
③权值更新:
④如果,则
,返回步骤2,进行前一层更新。对应输入层:
。
4、BP算法评述
◼优点:学习完全自主;可逼近任意非线性函数。
◼缺点:算法非全局收敛;收敛速度慢;学习速率α选择; 神经网络如何设计?
5、常用训练技巧
5.1 模型初始化
◼把所有权值在[-1,1]区间内按均值或高斯分布进行初始化。
◼Xavier初始化:为了使得网络中信息更好的流动,每一层输出的方差应该尽量相等。因此需要实现下面的均匀分布:
5.2 K折交叉验证
数据包括训练数据、验证数据、测试数据。通常三者比例为70%、15%、15%或60%、20%、20%。当数据很多时,训练和验证数据可适当减少。
原始训练数据被分成K个不重叠的子集。 然后执行K次模型训练和验证,每次在K−1个子集上进行训练, 并在剩余的一个子集(在该轮中没有用于训练的子集)上进行验证。 最后, 通过对K次实验的结果取平均来估计训练和验证误差。
5.3 权重衰减(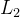 正则化)
正则化)
欠拟合指误差一直比较大,过拟合指在训练数据集上误差小而在测试数据集上误差大。

为防止过拟合和权值震荡,加入新的指标函数项:
第二项约束了权值不能过大。在梯度下降时,导数容易计算:
5.4 Dropout(暂退)
在整个训练过程的每一次迭代中,标准暂退法包括在计算下 一层之前将当前层中的一些节点置零。

6、求解方法
6.1 动量法
如果把原始的SGD想象成一个纸团在重力作用向下滚动,由于质量小受到山壁弹力的干扰大,导致来回震荡;或者在鞍点处因为质量小速度很快减为0,导致无法离开这块平地。动量方法相当于把纸团换成了铁球;不容易受到外力的干扰,轨迹更加稳定;同时因为在鞍点处因为惯性的作用,更有可能离开平地。

动量法公式如下:


6.2 自适应梯度算法
具有较大偏导的参数相应有一个较大的学习 率,而具有小偏导的参数则对应一个较小的学习率。这就是参数的自适应变化。具体来说,每个参数的学习率会缩放各参数反比于其历史梯度平方值总和的平方根。
AdaGrad是最基础的自适应梯度算法。它的问题在于学习率是单调递减的,训练后期学习率过小会导致训练困难, 甚至提前结束。因此需要设置一个全局的初始学习率。

RMSProp能解决AdaGrad方法中学习率过度衰减的问题。它使用指数衰减平均以丢弃遥远的历史,使其能够快速收敛;此外,RMSProp还加入了超参数𝜌控制衰减速率。

Adam在RMSProp方法的基础上更进一步。除了加入历史梯度平方的指数衰减平均(𝑟)外,还保留了历史梯度的指数衰减平均(𝑠),相当于动量。Adam行为就像一个带有摩擦力的小球,在误差面上倾向于平坦的极小值。






















 1178
1178

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








