0x11 栈

0x11 栈

栈是一种“先进后出”的线性数据结构。栈只有一端能够进出元素，我们一般称这一端为栈顶，另一端为栈底。添加或删除栈中元素时，我们只能将其插入到栈顶（进栈），或者把栈顶元素从栈顶取出（出栈）。

实现一个栈，支持查找栈中最小值的操作，要求时间复杂度为O(1)。

我们可以建立两个栈，一个栈A记录原本的数据，另一个栈B储存栈A中以栈底开头的的每段数据最小值，就像下面一样：

A: 9 2 1 5 3 0 2 <—

B: 9 2 1 1 1 0 0 <—

1.表达式计算

栈的一大用途是做算术表达式的计算。算术表达式通常有前缀、中缀、后缀三种表达方式。

中缀表达式，我们最常见的表达式，例如：3 * ( 1 - 2 )。

前缀表达式，又称波兰式，形如“op A B”，其中op是一个运算符，A，B是另外两个前缀表达式。例如：* 3 - 1 2。

后缀表达式，有又称逆波兰式，形如“A B op”，例如：1 2 - 3 *。

前缀和后缀表达式的值的定义是，先递归求出A，B的值，二者再做op运算的结果。这两种表达式不需要使用括号，其运算方案是唯一确定的。对于计算机来说，它最容易理解后缀表达式，我们可以使用栈来$O(N)$地求出它的值。

后缀表达式求法

1.建立一个用于存数的栈，逐一扫描该后缀表达式中的元素。

（1）如果遇到一个数，则把该数入栈。

（2）如果遇到运算符，就取出栈顶的两个数进行运算，然后把结果入栈。

2.扫描完成后，栈中恰好有一个元素，就是该后缀表达式的值。

如果想要计算机求解我们常用的中缀表达式的值，最快的方式就是把中缀表达式转化成后缀表达式，再使用上述方法求值。这个转化过程同样可以使用栈来$O(n)$完成。

中缀表达式转化成后缀表达式

1.建立一个用于存运算符的栈，逐一扫描该中缀表达式中的值。

（1）如果遇到一个数，输出该数。

（2）如果遇到左括号，把左括号入栈。

（3）如果遇到右括号，不断取出栈顶并输出，直到栈顶为左括号，然后把左括号出栈。

（4）如果遇到运算符，只要栈顶符号的优先级大于等于新符号，就不断取出栈顶并输出，最后把新符号入栈。优先级为乘除>加减>左括号。

2.依次取出并输出栈中所有的剩余符号，最终输出的序列就是与原中缀表达式等价的后缀表达式。

当然我们也可以不转化成后缀表达式，而是使用递归法直接求解中缀表达式的值，其时间复杂度为$O(N^2)$。

中缀表达式的递归求法

目标：求解中缀表达式S[1~N]的值

子问题：求解中缀表达式S的子区间表达式S[L~R]的值。

1.在L~R中考虑没有被任何括号包含的运算符：

（1）若存在加减号，选其中最后一个，分成左右两半递归，结果相加减，返回。

（2）若存在乘除号，选其中最后一个，分成左右两半递归，结果相乘除，返回。

2.若不存在没有被任何括号包含的运算符：

（1）若首尾字符是括号，递归求解S[L+1~R-1]，把结果返回。

（2）否则，说明区间S[L~R]是一个数，直接返回。

2.单调栈

如下图所示，在一个水平上方有若干个矩形，求包含与这些矩形的并集内部的最大矩形的面积（在下图中，答案就是阴影部分的面积），矩形个数$\le 10^5$。

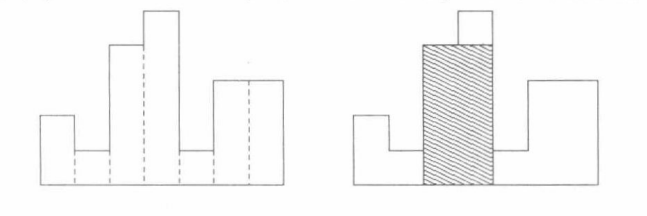
如果矩形的高度从左往右递增，我们可以尝试每个矩形的高度作为最终矩形的高度，并把宽度延伸到右边界，得到一个矩形，在所有这样的矩形中取面积的最大值就是答案。如下图所示：

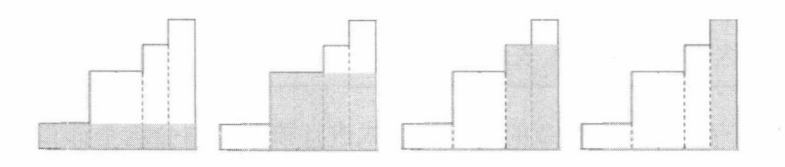
如果下一个矩形的高度小于上一个矩形的高度，那么该矩形想利用之前的矩形一起构成一块较大的面积时，这块面积的高度就不可能超过该矩形自身的高度。换句话说，在考虑完上图的四种情况后，下图中打叉的那部分面积就没有任何用处了。

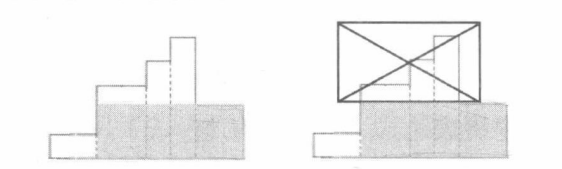
既然没有用，就把这些比该矩形高的矩形都删掉，用一个宽度累加、高度为该矩形自身高度的新矩形（就是上图的阴影部分）来代替。这样不会对后续的计算产生任何影响。于是我们维护的轮廓就变成了一个高度始终单调递增的矩形序列。

详细来说，我们建立一个栈，用来保存若干个矩形，这些矩形的高度是单调递增的，我们从左往右依次扫描每个矩形：

如果矩形比当前栈顶矩形高，直接入栈。

否则不断取出栈顶，直到栈为空或者栈顶矩形的高度比当前矩形小。在出栈过程中，我们累计被弹出的矩形宽度之和，并且每弹出一个矩形，就用它的高度乘上累计的宽度去更新答案。整个出栈过程结束，我们把一个高度为当前高度、宽度为累计宽度的新矩形入栈。

整个扫描结束，我们把栈中的剩余矩形依次弹出，按照与上面相同的方法更新答案。为了简化程序我们也可以增加一个高度为0的矩形a[n+1],以避免在扫描结束后栈中有剩余矩形。

long long ans=0;
int p=0;
a[n+1]=s[p]=0;
for(int i=1;i<=n+1;++i)
{
    if(a[i]>=s[p])
        s[++p]=a[i],w[p]=1;
    else
    {
        int width=0;
        while(s[p]>a[i])
        {
            width+=w[p];
            ans=max(ans,(long long)width*s[p]);
            --p;
        }
        s[++p]=a[i],w[p]=width+1;
    }
}

这就是著名的单调栈算法，时间复杂度为$O(n)$。借助单调性处理问题的思想在于及时排除不可能的选项，保持策略集合的高度有效性和秩序性，从而为我们做出决策提供更多的条件和可能方法。

实际应用：寻找到数组中一个数上一个或下一个更大数或更小数的位置。一个序列通过单调栈，我们可以找到序列中数A前面小于它的第一个数B。改成递减排列，也可以找到序列中数A前面大于它的第一个数B。也可以通过反向输入序列，找到序列中数A后面大于或小于它的第一个数B。