MPM（物质点法）算法

走366

已于 2024-11-21 19:39:12 修改

阅读量2.4k

点赞数 13

文章标签：算法

于 2024-11-21 19:37:48 首次发布

本文链接：https://blog.csdn.net/qq_61356662/article/details/143928260

版权

Stomakhin A, Schroeder C, Chai L, et al. A material point method for snow simulation[J]. ACM Transactions on Graphics (TOG), 2013, 32(4): 1-10.

这篇文章是MPM对图形学的第一次应用。

下面是对论文主要内容的提取

摘要

雪是一种模拟起来极具挑战性的自然现象。尽管图形学领域之前研究了雪的累积和渲染问题，但对雪动态的动画模拟仍未得到充分解决。此外，现有的固体和流体模拟技术在生成可信的雪的效果时存在困难，特别是对具有固体和流体双重性质的湿雪或密雪更是难以处理。因此，本文提出了一种全新的雪模拟方法，该方法结合了用户可控的弹塑性本构模型和混合欧拉-拉格朗日物质点法（MPM）。这种方法基于连续介质，其混合特性使我们能够使用规则的笛卡尔网格来自动处理自碰撞和断裂。此外，该方法自然支持基于网格的半隐式积分方案，该方案的条件数与拉格朗日粒子数量无关。我们通过展示复杂的角色交互中的各种雪现象，证明了我们方法的强大能力。

1. 引言

难点： 雪具有连续变化的相态，有时表现为刚性/变形固体，有时表现为流体。

贡献：

首先，我们开发了一种基于物质点法（MPM）的半隐式求解器，该方法专门用于高效处理复杂雪场景中出现的大范围材料刚度、碰撞和拓扑变化。
一种新颖的雪本构模型，该模型旨在实现对实际雪行为的直观用户控制。这一模型也旨在实现使用一个本构关系描述雪的多种行为相态的目标。为此，我们借鉴了工程学领域关于雪的丰富文献，并证明弹塑性处理是一种有效方式，能够处理包括流动、聚集、断裂等在内的多种行为之间的转换。

实际上，如果只需要学习MPM算法，可以忽略雪的模型的研究

需要了解什么叫半隐式求解器，以及包括显式和隐式求解器。

2. 相关工作

不可压缩流体（比如沙子、液体）的仿真使用FLIP算法效果不错，但也会出现一些问题。MPM扩展了FLIP算法，能够适应可压缩的计算。

雪的建模方法为弹塑性连续介质建模，这个可以追溯到Terzopoulos 和 Fleischer [1988] 在图形学中开创的可塑性和断裂的变形建模。

需要了解什么叫弹塑性连续介质建模。

3. 论文概述

雪动力学建模非常困难，这是由于雪的特性多变，通常由环境因素（如新鲜程度、水/冰含量等）引起。我们的模型忽略了根本原因，而是专注于通过现象学观察推导经验模型。尽管如此，我们的雪本构模型仍基于理论和工程应用设计的模型，保持了计算效率，同时捕捉到足够的几何细节。

物质点法（MPM） 是我们技术的核心。其本质上依赖于连续介质的近似，避免了对每个雪粒的建模需求。

我们选择 MPM 的原因在于它更好地处理雪的动力学。这类似于刚体模拟在处理无限刚度和不可压缩性时的效率。相比有限元网格（FEM）的大刚度矩阵，MPM 提供了一种更高效的模拟方式。

不同方法在模拟雪的四个重要性质（体积保持、刚性、塑性、断裂）方面的能力表如下：

雪的体积保持非常重要，尽管与液体不同，雪是可压缩的。然而，雪对体积变化的抵抗是多变的，我们在方法中将其建模为类似于普通基于网格的固体模拟。刚性同样重要，尽管 MPM（物质点法）在这一点上不如基于网格的弹性（变形梯度的精度较低），但它比基于网格的弹性更有效，因为变形梯度不会发生耗散，并且始终与位置保持同步。

塑性和断裂也能通过 MPM 得到很好地处理，这使得这种方法在模拟雪时非常有吸引力。对于塑性，MPM 几乎是理想的，因为变形梯度的不准确会累积为人为塑性。尽管基于网格的流体方法在塑性处理方面表现良好 [Goktekin et al., 2004]，MPM 在保持角动量方面表现更优。虽然基于网格的有限元法（FEM）可以处理塑性 [Bargteil et al., 2007]，但在极端变形下需要重新划分网格。相比之下，MPM 只需跟踪未网格化的粒子即可。

需要注意的是，MPM 在塑性和断裂方面的优势是以降低弹性精度为代价的，但对于雪的模拟而言，这是一个合理的折中。

4. 物质点法

开始进入公式推导环节了。

一个物体的变形可以被描述为从其未变形配置 $X$ 到变形配置 $x$ 的映射，映射的公式是 $x = \phi(\mathbf{X})$

其中变形梯度 $\mathbf{F} = \frac{\partial \phi}{\partial \mathbf{X}}$ ，其中变形 $\phi(\mathbf{X})$ 根据以下守恒定律演变：质量守恒、动量守恒以及弹塑性本构关系：

$\Large \frac{D \rho}{D t} = 0$ $\rho \frac{D \mathbf{v}}{D t} = \nabla \cdot \boldsymbol{\sigma} + \rho \mathbf{g}$ $\boldsymbol{\sigma} = \frac{1}{J} \frac{\partial \Psi}{\partial \mathbf{F}_E} \mathbf{F}_E^\mathrm{T}$

其中， $\rho$ 是密度， $t$ 是时间， $\mathbf{v}$ 是速度， $\boldsymbol{\sigma}$ 是 Cauchy 应力， $\mathbf{g}$ 是重力，是弹塑性势能密度， $\Psi$ 是弹性部分的变形梯度， $J = det(\mathbf{F})$

第一个方程是由于质量守恒，所以物质导数为0；

第二个方程是流体的动量方程推导，可以参考《计算流体力学基础及其应用》的第二章。

第三个方程本构模型会在后面讨论

材料点方法的基本思想是使用粒子（材料点）来追踪质量、动量和变形梯度。具体而言，粒子 $p$ 持有位置 $\mathbf{x_p}$ 、速度 $\mathbf{v_p}$ 、质量 $m_p$ 和变形梯度 $\mathbf{F}_p$ 。通过拉格朗日方式处理这些量，简化了对 $\Large \frac{D \rho}{D t}$ 和 $\rho \frac{D \mathbf{v}}{D t}$ 项的离散化。然而，粒子之间缺乏网格连接性，这使得应力项 $\nabla \cdot \boldsymbol{\sigma}$ 的求导复杂化。为解决这一问题，使用了规则的背景欧拉网格。

插值函数用于欧拉网格节点的力计算，这些函数以标准有限元方法的弱形式离散化项 $\nabla \cdot \boldsymbol{\sigma}$ 。我们采用 [Steffen et al. 2008] 提出的 一维三次 B 样条（one-dimensional cubic B-splines）作为网格基函数：

$N^h_i(\mathbf{x}_p) = N\left(\frac{1}{h}(x_p - ih)\right) N\left(\frac{1}{h}(y_p - jh)\right) N\left(\frac{1}{h}(z_p - kh)\right)$

其中 $i = (i, j, k)$ 是网格索引， $\mathbf{x}_p = (x_p, y_p, z_p)$ 是评估位置， $h$ 是网格间距，且

$N(x) = \begin{cases} \frac{1}{2}|x|^3 - x^2 + \frac{2}{3}, & 0 \leq |x| < 1, \\ -\frac{1}{6}|x|^3 + x^2 - 2|x| + \frac{4}{3}, & 1 \leq |x| < 2, \\ 0, & \text{otherwise}. \end{cases}$

为了简化记号，我们用 $w_{ip} = N^h_i(\mathbf{x}_p)$ 和 $\nabla w_{ip} = \nabla N^h_i(\mathbf{x}_p)$ 。这些插值函数用于自然地计算欧拉网格节点上的力。因此，必须首先从粒子转移质量和动量到网格节点，以便更新网格节点上的速度。然后，这一更新后的速度以 FLIP 或 PIC 的方式转回粒子。传递过程使用插值权重 $w_{ip}$ 。

需要了解为什么使用这个B-splines，其它的B-splines是什么形式？

需要了解基于拉格朗日粒子和欧拉网格的PIC和FLIP算法。

4.1 MPM算法流程

1. 将粒子数据栅格化到网格

粒子质量->网格质量粒子速度->网格速度

$m_i^n = \sum_p m_p w_{ip}^n$ $\mathbf{v}_i^n = \sum_p \mathbf{v}_p^n m_p w_{ip}^n/m_i^n$

2. 计算粒子体积和密度

估算一个格子单元密度为 $m_i^0/h^3$ ，并将其加权回粒子作为 $\rho_p^0 = \sum_i m_i^0 w_{ip}^0/h^3$

由此估算粒子体积 $V_p^0 = m_p/\rho_p^0$

3. 计算网格力（后面节的公式）

其中 $\hat{x}_i = x_i$

4. 更新网格的速度，处理网格的碰撞

碰撞在第8节详细讲解。

5. 求解线性系统

如果是半隐式计算，需要用到下面的方程；如果仅仅是显式计算，直接赋值 $\mathbf{v}_i^{n+1} = \mathbf{v}_i^*$

6. 更新变形梯度

其中，

第7节详细描述了 $\mathbf{F}$ 的弹性和塑性部分的更新规则。

7. 更新粒子速度

其中PIC部分的速度 $\mathbf{v}_{\text{PIC}_p}^{n+1} = \sum_i \mathbf{v}_i^{n+1}w_{ip}^n$

FLIP部分速度 $\mathbf{v}_{\text{FLIP}_p}^{n+1} = \mathbf{v}_p^n + \sum_i(\mathbf{v_i}^{n+1} - \mathbf{v_i}^n)w_{ip}^n$

粒子速度结合了PIC和FLIP算法，光使用PIC会导致能量耗散（角动量不守恒），光使用FLIP会不稳定（详细的说不上来，只是看APIC论文里面简要说明了）。

8. 粒子的碰撞

看第8节讲解

9. 更新粒子位置

这个公式也许就是半隐式求解。

5. 本构模型

在乘性塑性理论中，通常将变形梯度 $\mathbf{F}$ 分解为弹性部分 $\mathbf{F}_E$ 和塑性部分 $\mathbf{F}_P$ ，即 $\mathbf{F} = \mathbf{F}_E \mathbf{F}_P$ 我们通过弹塑性能量密度函数定义了我们的本构模型：

其中弹性部分由 [Stomakhin et al. 2012] 的固定协转能量密度给出，且 Lamé 参数为塑性变形梯度的函数：

其中这里， $\lambda _0$ 和 $\mu _0$ 是初始 Lamé 系数， $\xi$ 是无量纲塑性硬化参数。

我们根据变形梯度的奇异值定义材料的弹性和塑性行为。定义了临界压缩 $\theta _c$ 和拉伸 $\theta _s$ 阈值，用于描述材料开始塑性变形（或断裂）的条件。换句话说， $\mathbf{F}_E$ 的奇异值被限制在区间 $[1-\theta_c, 1-\theta_s]$ 。通俗点说，当超过这个阈值吗，材料就会断裂或塑性变形。

雪仿真的参数设置如下：

材料属性依据公式 (2) 调整，增加其在压缩（紧实）下的强度，并在拉伸（断裂）下减弱，从而实现逼真的雪现象。

临界压缩 $\theta_c$ 和拉伸 $\theta_s$ 决定材料何时开始断裂（值越大，材料越块状；值越小，材料越粉状）。硬化系数 $\xi$ 决定材料断裂变为塑性（更大表示更脆；更小表示更具韧性）。干燥和粉状雪具有更小的临界压缩和拉伸阈值，而湿润和块状雪相反。冰雪具有更高的硬化系数和杨氏模量，而其相对的会生成泥状雪。

6. 基于应力的力和线性化

弹性势能可以用能量密度 $\Psi$ 表示为:

其中 Ω⁰ 是材料的未变形构型。MPM(材料点法)对基于应力的力的空间离散化等价于对该能量关于欧拉网格节点材料位置的离散近似的微分。但是,我们实际上并不变形欧拉网格,所以我们可以认为网格节点位置的变化是由网格节点速度决定的。也就是说,如果 $\mathbf{x}_i$ 是网格节点 $i$ 的位置,那么 $\hat{\mathbf{x}}_i = \mathbf{x}_i + \Delta t\mathbf{v}_i$ 就是该网格节点在当前速度 $\mathbf{v}_i$ 下的变形位置。如果我们用 $\hat{\mathbf{x}}$ 表示所有网格节点 $\hat{\mathbf{x}}_i$ 的向量,那么弹性势能可以写作:

其中 $V_p^0$ 是粒子 p 最初占据的体积。 $\mathbf{F}_{Pp}^n$ 是 t =n时刻粒子 p 力的塑性部分,而 $\mathbf{F}_{Ep}$ 是与 $\hat{\mathbf{x}}$ 相关的力的弹性部分,如[Sulsky et al. 1995]所示:

基于这种约定,MPM对基于应力的力的空间离散化给出:

也就是说, $\mathbf{f}_i(\hat{\mathbf{x}})$ 是由弹性应力作用在网格节点 $i$ 上的力。这通常用柯西应力表示，表示为：

其中 $V_p^n = J_p^n V_p^0$ 是粒子 p 在 $t^n$ 时刻占据的体积。

我们强调 MPM 空间离散化与弹性势能的这种关系,因为我们想通过隐式方法来演化网格速度 $\mathbf{v}_i$ 。通过这种约定,我们可以对更新的弹性部分利用势能对 $\hat{\mathbf{x}}$ 的 Hessian 来进行隐式步进。这个 Hessian 作用在任意增量 $\delta \mathbf{u}$ 上可表示为:

其中，

这里记号 $A = C:D$ 表示 $A_{ij} = C_{ijkl}D_{kl}$

6.1 半隐式更新

我们将弹塑性响应定义为欧拉网格节点的材料位置 $\hat{\mathbf{x}}_i = \mathbf{x}_i + \Delta t\mathbf{v}_i$ 。但是,如前所述,我们从不变形该网格。因此,我们可以将 $\hat{\mathbf{x}} = \hat{\mathbf{x}}(\mathbf{v})$ 理解为由 $\mathbf{v}$ 定义的 $\hat{\mathbf{x}}(\mathbf{v})$ 。基于此,我们使用以下记号、 and

使用这些导数,我们形成隐式更新 $\mathbf{v}_i^{n+1} = \mathbf{v}_i^n + \Delta tm_i^{-1}((1-\beta)\mathbf{f}_i^n + \beta \mathbf{f}_i^{n+1}) \approx \mathbf{v}_i^n + \Delta tm_i^{-1}(\mathbf{f}_i^n + \beta \Delta t \sum_j \frac{\partial \mathbf{f}_i}{\partial \mathbf{x}_j}\mathbf{v}_j^{n+1})$ 。这导致求解 $\mathbf{v}_j^{n+1}$ 的(质量)对称系统:

右边部分为：

这里 β 在显式(β=0)、梯形法(β=1/2)和后向欧拉(β=1)之间选择。

7. 变形梯度更新

我们首先临时定义如式(4)所示,并且使得最初所有的变化都归因于变形梯度的弹性部分:

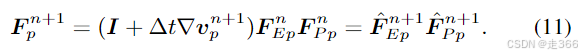
下一步是取 $\mathbf{F}_{Ep}^{n+1}$ 超过临界变形阈值的部分,并将其推入 $\mathbf{F}_{Pp}^{n+1}$ 。我们计算奇异值分解 ,然后将奇异值限制在允许范围内 $\Sigma_p = clamp(\Sigma_p,[1-\theta_c,1+\theta_c])$ 变形梯度的最终弹性和塑性分量计算为:

很容易验证

8. 物体碰撞

我们在每个时间步长中处理两次与碰撞体的碰撞。第一次是在力作用于网格速度 $\mathbf{v}_i^*$ 之后立即进行。在半隐式积分的情况下，这会影响线性系统的右侧，并且在求解过程中会投影出与碰撞网格节点相对应的自由度。我们在更新位置之前对粒子速度 $\mathbf{v}_p^{n+1}$ 再次应用碰撞，以解决由于插值导致的粒子和网格速度之间的微小差异。在每种情况下，碰撞处理都以相同的方式进行。我们的所有碰撞都是非弹性的。

碰撞物体表示为水平集，这使得碰撞检测（φ ≤ 0）变得简单。在发生碰撞的情况下，先计算局部法线 $\mathbf{n} = \nabla \varphi$ 和物体速度 $\mathbf{v}_{co}$ 。首先，将粒子/网格速度 $\mathbf{v}$ 转换到碰撞物体的参考系中： $\mathbf{v}_{rel} = \mathbf{v }- \mathbf{v}_{co}$ 。如果物体正在分离 $\mathbf{v}_n = \mathbf{v}_{rel} \cdot \mathbf{n } \geqslant 0$ ，则不需要应用碰撞。令 $\mathbf{v}_t = \mathbf{v}_{rel} - \mathbf{n}\mathbf{v}_n$ 为相对速度的切向分量。如果需要粘着冲量 $(\left \| \mathbf{v}_t \right \| \leqslant -\mu \mathbf{v}_n)$ ，那么我们直接令 $\mathbf{v}'_{rel} = 0$ ，表示已应用碰撞。否则，我们应用动态摩擦，且其中 $\mu$ 是摩擦系数。最后，我们将碰撞后的相对速度转换回世界坐标系： $\mathbf{v}' =\mathbf{ v}'_{rel} + \mathbf{v}_{co}$

我们使用了两种类型的碰撞物体：刚体和变形体。在刚体情况下，我们存储一个静态水平集和一个随时间变化的刚体变换，我们可以用它在任何点计算 $\phi$ 、 $\mathbf{\mathbf{}n}$ 和 $\mathbf{v}_{co}$ 。在变形情况下，我们加载水平集关键帧并插值，类似于[Selle et al. 2008]使用的 $\phi(x, t + \gamma \Delta t) = (1 - \gamma) \phi(x - \gamma \Delta t v_{co}, t) + \gamma \phi(x + (1 - \gamma) \Delta t v_{co}, t + \Delta t),$ ，不同的是我们计算速度为 $v_{co} = (1 - \gamma) v(x, t) + \gamma v(x, t + \Delta t),$ 而不是平均速度。

最后，在我们想要雪粘附到垂直或悬挂表面的情况下，我们使用一种粘性碰撞。在这种情况下，库仑摩擦是不够的，因为法向相对速度将为零（垂直）或为正（悬挂且由于重力分离）。我们通过无条件地将与这些表面碰撞的 $\mathbf{v}'_{rel}$ 设置为 0 来实现这种效果。

9. 渲染

研究人员通过应用散射和辐射传输理论测量了散射特性（参见[Wiscombe and Warren 1980]），这在图形学中也很流行（参见[Nishita et al. 1997]）。我们的离散笛卡尔网格测量密度相对于材料粒子，这为我们提供了一种显示松散和紧密堆积的雪之间的视觉变化的方法。这给予我们相对于表面或纯粒子基础方法的渲染优势。

在渲染时，我们使用第4节中的相同核函数将最终模拟的材料点重新栅格化到模拟网格上，但改进的抗锯齿效果可以通过使用更好的核函数在完全不同的网格上获得。我们采用体积路径追踪器来求解体积散射方程，使用亨尼-格林斯坦相函数来近似冰晶的米氏散射理论。我们通常使用均值余弦 g = 0.5 来获得前向散射，消光系数 σt = 724m⁻¹，以及散射反照率 σs/σt = [0.9, 0.95, 1.0]，其中 σs 是散射系数。

10. 结果

我们模拟了各种示例来展示我们方法的威力。我们的本构模型结合了压缩性、塑性和硬化，可以自动处理断裂和堆积雪的特征性粘着效应。

下述表列出了每个示例的模拟时间和分辨率。对于所有示例，我们都是将粒子随机播撒到需要填充雪的体积中，并给它们相同的初始参数。我们发现每个网格单元使用4-10个粒子（对于初始紧密堆积的雪）可以产生合理的结果。此外，我们发现不需要进行任何粒子的重新播撒，我们还优化了网格操作，使其仅在粒子的插值半径重叠的节点上进行。因此，我们的计算量与粒子数量成正比，也就等同于被占据的网格单元数量。

在某些情况下，我们使用了每个粒子定义的空间变化本构参数来获得更真实的效果。例如，雪球的外部被制作得更硬更重，刚度按照噪声模式变化以获得块状断裂。这模仿了我们在现实世界中对雪球的实验。同样，对于行走角色，顶层被设置得更僵硬和脆，以模拟夜间温度下降的效果。

虽然简单，但显式更新方案需要很严格的时间步长才能保持稳定；通常需要 Δt ≈ 10⁻⁵ 才能获得合理的模拟行为。相比之下，我们的半隐式方法限制较少，对于本文提供的所有示例允许 Δt ≈ 0.5×10⁻³。半隐式更新步骤产生一个（质量）对称系统(9)，我们使用共轭残差法求解。在实践中，我们发现只需要10-30次迭代，且无需预处理，这与网格分辨率或粒子数量无关。

11. 讨论与结论

与FLIP的比较：不可压缩FLIP [Zhu and Bridson 2005]已成为图形学中模拟液体的极其流行的方法，原因与MPM有用的原因相似：它易于实现，能保持质量，并将网格和粒子混合使用，以获得每种表示方法的最佳特征。两种方法的基本本质都是使用背景网格作为计算中涉及非局部信息传递的草稿本，以加速和稳定计算。两种方法的主要区别在于不可压缩FLIP将不可压缩性作为约束强制执行，而MPM允许由更一般的本构模型支配的动力学。Zhu和Bridson [2005]整合了一些应力和应变的概念（与刚性分组技术一起）来获得沙子的一些本构建模；然而，它不如MPM方法灵活。可以将MPM [Sulsky et al. 1995]和不可压缩FLIP [Zhu and Bridson 2005]视为FLIP [Brackbill and Ruppel 1986]在可压缩流动原始用途之外的推广。有趣的是，Zhu和Bridson在他们的论文中提到了MPM，但认为它太慢。我们的方法通过使用半隐式时间积分和并行化解决了对MPM的这一批评。

局限性：我们的模型产生了大量令人信服的例子，但仍有许多工作要做。我们的许多参数都是手动调整的，将其校准到测量模型会很有趣。我们还忽略了与空气的相互作用，这对粉雪和雪崩来说很重要。渲染时的锯齿化有时是一个问题，这可以通过更好的过滤或采用更复杂的栅格化技术来处理。例如，我们希望尝试[Yu and Turk 2010]的各向异性核方法。我们也对扩展我们的工作到沙子模拟甚至一般断裂感兴趣。此外，使用自适应稀疏网格可以为未受影响的节点节省内存，这将节省内存但不影响计算，因为我们已经不对这些节点进行迭代。同样，使用模拟细节层次技术可以减少雪已经沉降区域的运行时间。我们也对通过CPU SIMD或GPGPU技术进行硬件加速感兴趣。

结论：我们提出了一个用于雪模拟的本构模型和模拟技术。我们的方法展示了各种雪的行为，特别是，它是第一个处理密实和湿雪丰富性的方法。此外，材料点法为连续介质力学提供了一种有趣的新技术，这可能会激发图形学领域的额外研究。