（详细图解）KMP算法（C语言）------可算领悟了这个由三位前辈研究的算法

黑夜里的小夜莺

已于 2022-10-24 10:02:23 修改

阅读量4.1k

点赞数 38

分类专栏：算法数据结构文章标签： java 开发语言 1024程序员节

于 2022-10-23 22:04:20 首次发布

本文链接：https://blog.csdn.net/qq_61959780/article/details/127466800

版权

数据结构同时被 2 个专栏收录

9 篇文章 29 订阅

订阅专栏

算法

3 篇文章 0 订阅

订阅专栏

1、主串、子串从数组索引为 1 处开始存储字符

2、主串、子串从数组索引为 0 处开始存储字符

3、例题

3、KMP模式匹配算法的改进

（1）主串、子串从数组索引为 1 处开始存储字符编辑

（3）例题

四、测试程序

（1）朴素的模式匹配算法（第一种写法）

（2）KMP模式匹配算法（第二种：主串、子串从数组索引0处开始）

五、参考资料

前言

写这份博客主要是帮助那些对KMP算法有些迷惑的人，同时也是自己的一份笔记，为了写这份博客自己也参考一些资料，整篇博客有点长，希望你们看这篇博客能坚持下去，加油喔！！！！

一、简介KMP算法

KMP算法是由 D.E.Knuth、J.H.Morris和V.R.Pratt三位前辈（其中Knuth 和 Pratt共同研究，Morris独立研究）发表的一个模式匹配算法，可以大大避免重复遍历的情况，我们把它称之为克努特-莫里斯-普拉特算法（由三位前辈名字命名的算法），简称KMP算法。在这里，我对三位前辈表示敬佩，感谢他们能研究出如此优秀的算法。

二、朴素的模式匹配算法

在介绍KMP算法前，我们先了解下为什么要用KMP算法。

第一种朴素的模式匹配算法的写法

首先，咱们先看下面这种不依赖其他串操作的暴力匹配算法——朴素的模式匹配的算法。其算法源码如下：

int Index(char* str, char* instr, int strlength, int instrlength)
{
	int i = 0, j = 0;
	while (i < strlength && j < instrlength)
	{
		if (str[i] == instr[j])
		{
			++i;   // 比较后续的字符
			++j;
		}
		else
		{
			i = i - j + 1; // 指针后退重新开始匹配
			j = 0;  // 重新指向模式串的第一个字符
		}
	}
	if (j >= instrlength)
		return i - instrlength;
	else
		return 0;
}

其算法思想为：从主串 str 的第一个字符起，与模式串 instr 的第一个字符比较，若相等，则继续逐个比较后续的字符；否则从主串的下一个字符起，重新和模式串的字符比较；以此类推，直至模式串 instr 中的每个字符依次和主串 str 中的一个连续的字符序列相等，则称匹配成功。

在这里我简要介绍一下上面的 else 语句块的语句（即指针后退重新开始匹配），怕有些不懂的人，因此做此介绍。

{
    i = i - j + 1; // 指针后退重新开始匹配
	j = 0; // 重新指向模式串的第一个字符
}

在这里的 i = i - j + 1 的原因如下：

当开始的主串第 i 个字符与模式串的第 0 个字符（数组的索引为0对应 instr的第一个字符）相等时，进入 if 语句块二者同时自增，直到主串的第 i + n 个与模式串的第 0 + n（由于j是从数组索引为0的地方开始匹配的）个字符不同时，便进入了 else 语句块，此时一共匹配了 n 个字符（n小于模式串的长度），i 的值为 i + n，j 的值为 n，故 i = i - j + 1 = i + n - n + 1 = i + 1，相当于刚开始匹配成功的位置向后移。

咱们用图来验证上面的推理：

刚开始 i = 0，j = 0，到 i = 0 + 2 = 2 和 j = 0 + 2 = 2处字符不相等，一共匹配了 n = 2 个字符（匹配失败），故 i = i - j + 1 = 1，即 i 从刚开始匹配成功的位置（i=0处）,向后移了 1 位，即下次从主串的第 2 个字符（i= 1）与模式串的第一个字符相比较（j = 0）。

第二种朴素的模式匹配算法的写法

可能大家也看过下面的这种朴素的模式匹配算法的源码。

int Index(char* str, char* instr, int strlength, int instrlength)
{
	int i = 1, j = 1;
	while (i <= strlength && j <= instrlength)
	{
		if (str[i] == instr[j])
		{
			++i;   // 比较后续的字符
			++j;
		}
		else
		{
			i = i - j + 2; // 指针后退重新开始匹配
			j = 1;  // 重新指向模式串的第一个字符
		}
	}
	if (j > instrlength)
		return i - instrlength;
	else
		return 0;
}

这种的是数组索引为 0 处不存储字符的写法（索引为0 处可能存储着这个字符串的长度，或者啥都不存储就是浪费一个空间），即从数组索引为 1 处开始存储字符串，其算法思想和从数组索引为 0 处开始存储字符串的算法思想一样。

算法思想：从主串 str 的第一个字符起，与模式串 instr 的第一个字符比较，若相等，则继续逐个比较后续的字符；否则从主串的下一个字符起，重新和模式串的字符比较；以此类推，直至模式串 instr 中的每个字符依次和主串 str 中的一个连续的字符序列相等，则称匹配成功。

在数组索引为1处开始存储字符，其 i = i - j + 2（不是加1喔），在这里也是解释一下原因。

else
{
	i = i - j + 2; // 指针后退重新开始匹配
	j = 1;  // 重新指向模式串的第一个字符
}

当开始的主串第 i 个字符与模式串的第 1 个字符（数组的索引为1对应 instr的第一个字符）相等时，进入 if 语句块二者同时自增，直到主串的第 i + n 个与模式串的第 1 + n（由于j是从数组索引为1的地方开始匹配的）个字符不同时，便进入了 else 语句块，此时一共匹配了 n 个字符（n小于模式串的长度），i 的值为 i + n，j 的值为 1 + n，故 i = i - j + 2 = i + n - n - 1 + 2 = i + 1，相当于刚开始匹配成功的位置向后移。

咱们也是用图验证上面的推理：

刚开始 i = 1，j = 1，到 i = 1 + 2 = 3 和 j = 1 + 2 = 3处字符不相等，一共匹配了 n = 2 个字符（匹配失败），故 i = i - j + 2 = 2，即 i 从刚开始匹配成功的位置（i=1处）,向后移了 1 位，即下次从主串的第 2 个字符（i= 2）与模式串的第一个字符相比较（j = 0）。

下面我用这种写法的朴素的模式匹配算法来做一个例子。

一个例子

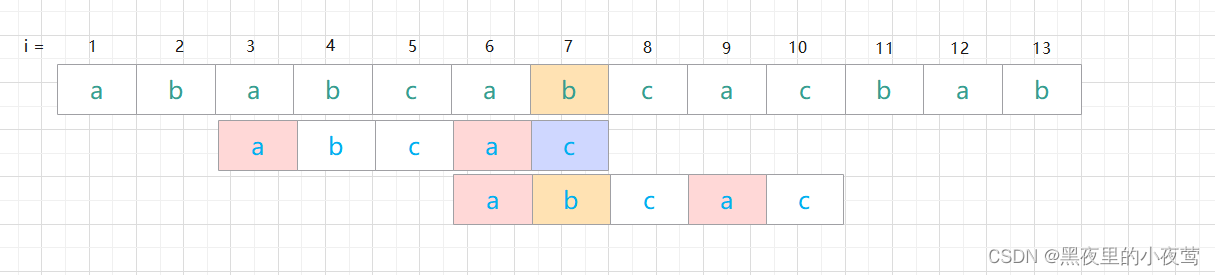
在主串 str = 'ababcabcacbab' 中找出模式串（子串） instr = 'abcac' 在其中的位置。

第一次匹配：

在 i = 3处匹配失败，此时 j = 3 < 5（模式串 instr 长度），故需要模式串向右一位（右移后 i = 2, j = 1），又重新开始匹配。

第二次匹配：

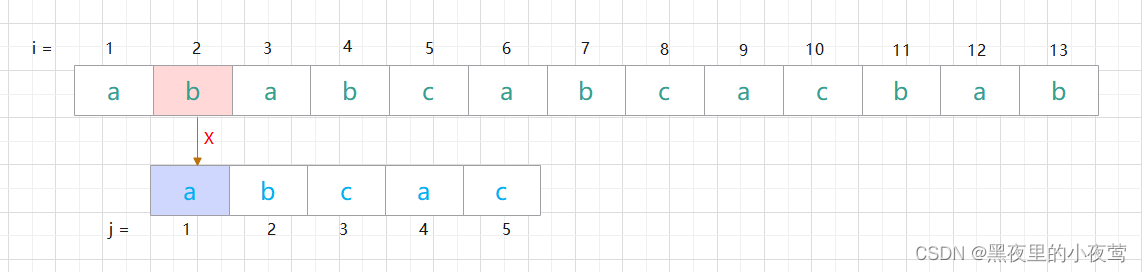
直接刚开始匹配就失败，故又需模式串向右移一位（右移后 i = 3, j = 1） ,并重新开始匹配。

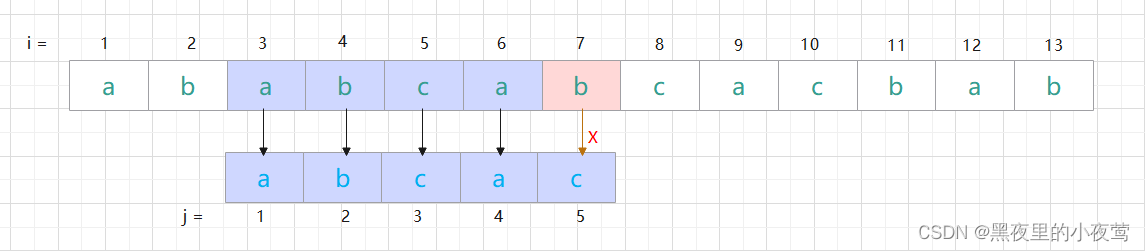
第三次匹配：

在 i = 7处匹配失败，此时 j = 5 = 5（模式串长度，不大于匹配失败），需模式串向右移一位（右移后 i = 4, j = 1） ,并重新开始匹配。

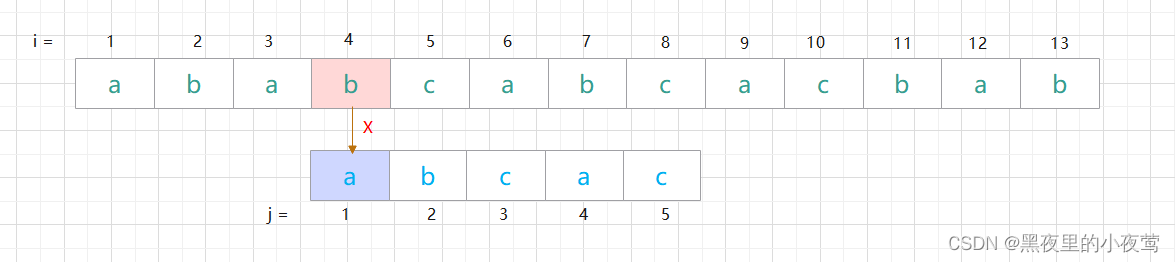
第四次匹配：

直接刚开始匹配就失败，故又需模式串向右移一位（右移后 i = 5, j = 1） ,并重新开始匹配。

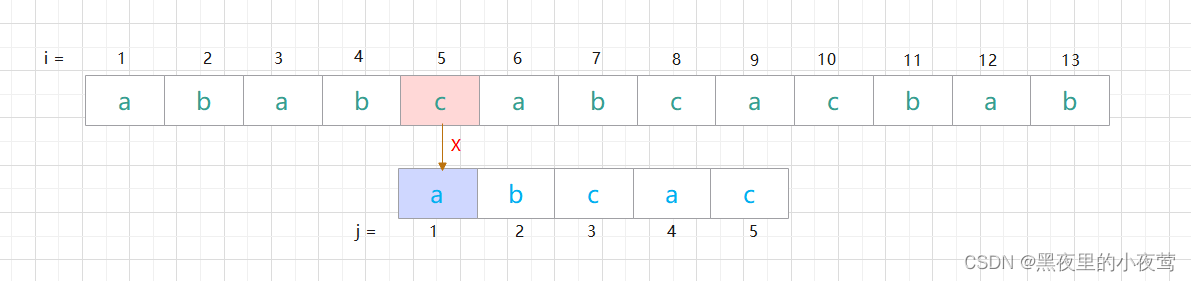
第五次匹配：

直接刚开始匹配就失败，故又需模式串向右移一位（右移后 i = 6, j = 1） ,并重新开始匹配。

第六次匹配：

匹配成功，此时 i = 11，j = 6 > 5。返回 index = i - instrlength = 11 - 5 = 6，即模式串 instr 从主串的第六个字符开始。

这个例子也可以用第一种的写法来做（画图过一遍算法流程），都是类似的，有兴趣可以试试。

第三总结

这两种算法基本没啥区别（算法思路一致），在使用时注意一些细节即可（如两者else块语句中的 i 的改变不同，while循环的判断条件不同等），看清况使用这两种算法，一般第一种写法为主。我自己认为第二种算法主要的设计原因就是数组的索引是几，即代表字符串的第几个字符，符合我们表述吧。

上面的两种写法的朴素模式匹配的最坏时间复杂度为O(nm)（即模式串在主串的最后面处），其中 n：主串的长度，m：模式串的长度。当主串为'0000000000000000000000000000000000000000000001'，模式串为'0000001'时，由于模式中前6个字符均为‘0’，主串中前45个字符均为‘0’，每次匹配都是比较到模式的最后一个字符时才发现不等，指针 i 回溯40次，总比较次数为 40 x 7 = 280 次。

三、KMP算法

我们发现上面的算法比较次数太多了，最坏的情况要比较 nm 次，那咱们可不可以减少比较次数呢？当然可以的，这就是咱们KMP算法的用武之处，在上面的比较中，我们发现 i = 7、j = 5的字符比较不等，于是又从 i = 4、j = 1重新开始比较。然后，仔细观察会发现，i = 4 和 j = 1, i = 5和 j = 1及 i = 6 和 j = 1这三次比较都是不必进行的。从第三次部分匹配的结果可知，主串中的第 4、 5和6个字符是 'b'、'c' 和'a'（即模式串中的第2、3和4个字符），因为模式中第一个字符是 'a'，因此无须和这3字符进行比较（'a'和'b'、'c'不同，比较后肯定比较失败，'a'（模式的第1个字符）和'a'（模式的第4个字符）相同，也不同比较），而只需要将模式串向右移3个字符的位置，继续进行 i = 7、j = 2时的比较即可。

直接进行 i = 7、j = 2的比较：

在暴力匹配中，每次匹配失败都是模式后移一位再从头开始比较。而每次已匹配相等的字符序列是模式的某个前缀，这次频繁的重复比较相当于模式串的不断地进行自我比较，这就是其低效率的根源，（即我们在朴素的模式匹配算法中主串的 i 值是不断地回溯来完成的）。而我们通过分析发现其实这种回溯是可以省略的——正所谓好马不吃回头草，我们的KMP模式匹配算法就是为了让这没必要的回溯不发生。（即如果已匹配相等的前缀序列中有某个后缀正好是模式的前缀，那么就可以将模式向后滑动到与这些相等字符对齐的位置，主串 i 指针无须回溯，并从该位置开始继续比较。而模式向后滑动位数的计算仅与模式的本身的结构有关，与主串无关。——到这可能有些人会理解起来有些困难，不用着急，我们带着疑问向后看）。

1、字符串的前缀、后缀和部分匹配值

咱们之前上文说的前缀、后缀可能有些人不理解，咱们现在就介绍一下这两个概念。前缀：除最后一个字符外，字符串的所有头部子串；后缀：除第一个字符外，字符串的所有尾部子串。而我们还增加一个概念——部分匹配值：字符串的前缀和后缀的最长相等前后缀长度。

下面以'ababa'为例进行说明：

'a' 的前缀和后缀都为空集，最长相等前后缀长度为 0.
'ab' 的前缀为{ a }，后缀为{ b }，{ a } $\wedge$ { b } = $\varnothing$ ，最长相等前后缀长度为 0。
'aba' 的前缀为{ a, ab }，后缀为{ a, ba }，{ a, ab } $\wedge$ { a, ba } = { a }，最长相等前后缀长度为1。
'abab' 的前缀{ a, ab, aba } $\wedge$ 后缀{ b, ab, bab } = { ab }，最长相等前后缀长度为 2.
'ababa' 的前缀{ a, ab, aba, abab } $\wedge$ 后缀 { a, ba, aba, baba} = {a, aba}，公共元素有两个，最长相等前后缀长度为 3 。

故字符串 'ababa' 的部分匹配值为 00123.

咱们此时就有个疑问——这个部分匹配值有什么作用呢？

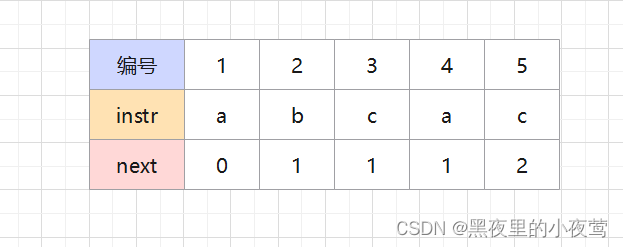
回到上面的那个例子——主串为 'ababcabcacbab' ，子串 'abcac'。利用上述方法容易写出子串 'abcac' 的部分匹配值为 00010，将部分匹配值写成数组形式得出部分匹配值（Partial Match，PM）的表。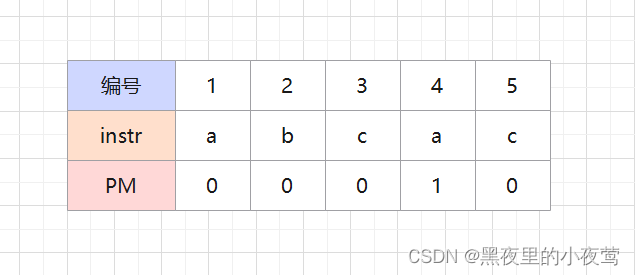

下面用PM表来进行字符串的匹配：

(在匹配前我们需要知道下面这公式，这个公式用于算出子串（模式串）需要向后移动的位数.。)

移动位数 = 已匹配的字符数 - 对应的部分匹配值（最后一个匹配成功的字符对应的匹配值）

第一次匹配过程：

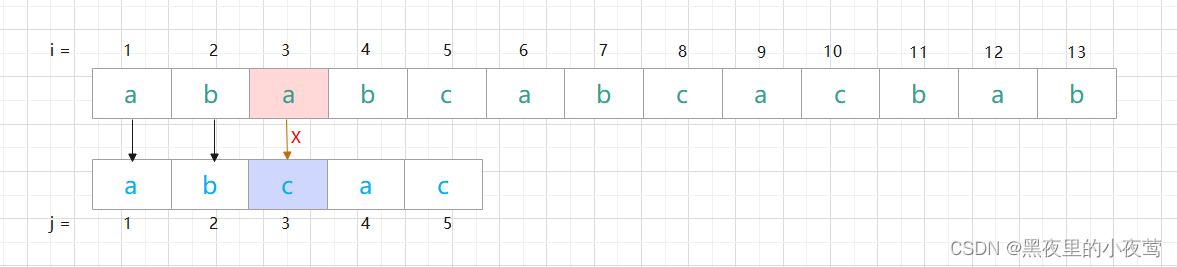发现 c 与 a 不匹配，前面的 2 个字符 'ab' 是匹配的，查表可知，最后一个匹配字符 b 对应的部分匹配值为 0，因此按照上面的公式计算出子串需要向后移动的位数：2 - 0 = 2，故将子串向后移动 2 位，如下进行第二次匹配。

第二次匹配：

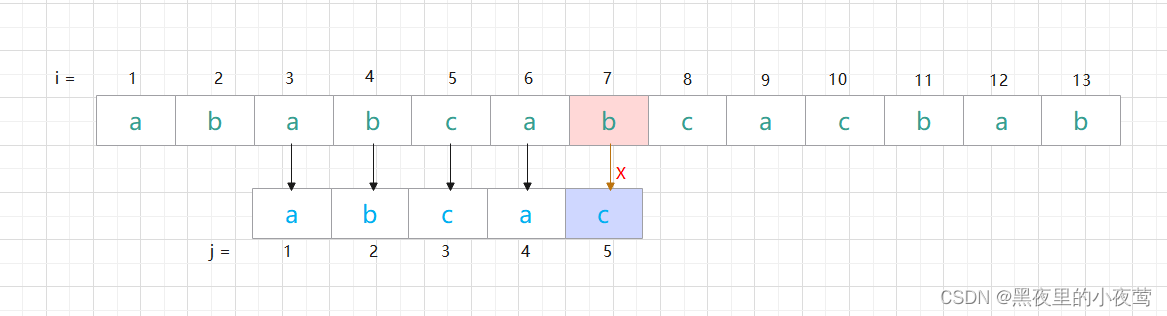发现 c 与 b 不匹配，前面 4 个字符 'abca' 是匹配的，最后一个匹配字符 a 对应的部分匹配值为1,4 - 1 = 3，将子串向后移动3位，如下进行第三次匹配。

第三次匹配：

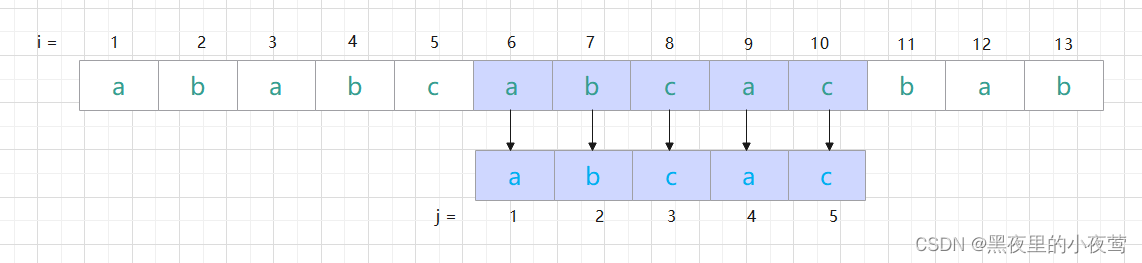子串全部比较完成，匹配成功。整个匹配过程中，主串始终没有回退，故KMP算法可以在O(n + m)的时间数量级上完成串的模式匹配操作，大大提高了匹配效率。

总结：子串的如何移动的

在进行某次匹配发生失败时，如果对应的部分匹配值为 0，那么表示已匹配相等序列中没有相等的前后缀，此时移动的位移数最大，直接将子串的首字符后移到主串 i 位置进行下一次比较（如上面的第一次匹配，直接子串的首字符 'a' 与主串的 i = 3 处的字符 'a' 进行比较）。

如果已匹配相等序列中存在最大相等的前后缀（可理解首尾重合），那么将子串向右滑动到和该相等前后缀对齐（这部分字符下次显然不需要比较，因为在这次比较完了），然后从主串 i 位置进行下一次比较。（如上面第二次匹配，直接子串中的字符 'b' 和主串 i = 7进行比较）

其实想也明白上面的公式：移动位数 = 已匹配的字符数 - 对应的部分匹配值（最后一个匹配成功的字符对应的匹配值）。对应的部分匹配值为 0，那么移动的位数肯定最大，已匹配的字符数不需要减少，最大移动位数就等于已匹配的字符数。

2、KMP算法的原理

通过上面的学习，我们学会了怎么计算字符串的部分匹配值、怎样利用子串的部分值快速地进行字符串的匹配操作，但上面公式移动位数 = 已匹配的字符数 - 对应的部分匹配值（最后一个匹配成功的字符对应的匹配值）的意义是什么呢？

如下图：

当 c 与 b不匹配时，已匹配 'abca'的前缀 a 和后缀 a为最长公共元素。已知前缀a 与b、c均不同，与后缀 a相等，故无须与比较，直接将子串移动 “已匹配的字符数 - 对应的部分匹配值”位（即用子串前缀后面的元素与主串匹配失败的元素开始比较即可）。如下图：

故上面公式的意义：让我们不需要进行不必要的匹配，减少比较次数。

到这里，我们对算法进行改进有没有一些想法呢？如果想到改进算法要利用到上面的公式，说明你很不错sai，接下来进行改进算法。

算法改进

已知：右移位数 = 已匹配的字符数 - 对应的部分匹配值（最后一个匹配成功的字符对应的匹配值）

写成：Move = （j - 1） - PM[ j-1 ]。（这里是子串从数组索引为 1 处开始存储字符）。

如果是子串从数组索引为 0 处开始存储字符上面的公式改为 Move = j - PM[ j-1 ]。

推出一般规律，若子串从数组为 i 处开始存储字符，则 Move = （j - i) - PM[ j-1 ]。其实对子串从数组索引为 i 开始存储字符其实主要是对上面公式（右移位数 = 已匹配的字符数 - 对应的部分匹配值（最后一个匹配成功的字符对应的匹配值））进行符号化，改变的只是已匹配的字符数的求法，这些不同的公式表达也就是上面公式的意思，其内涵都是一致的。

在这里咱们介绍两种：

主串、子串从数组索引为 1 处开始存储字符——Move = （j - 1) - PM[ j-1 ]
主串、子串从数组索引为 0 处开始存储字符——Move = j - PM[ j-1 ]

大多数有关数据结构的书籍基本也就是这两种。

使用部分匹配值时，每当匹配失败，就去找它前一个元素的部分匹配值，这样使用起来有些不方便，既然不方便，那咱们就让它方便起来，将PM表右移一位，这样哪个元素匹配失败，直接看它自己的部分匹配值即可。

将上面例子中的字符串 'abcac' 的PM表右移一位，就得到了 next 数组：

1、主串、子串从数组索引为 1 处开始存储字符

2、主串、子串从数组索引为 0 处开始存储字符

这两种基本没啥区别，只是编号不同（对应数组的索引），其对应的字符所对应的next值都是一致的。

而可以这么做的原因如下：

第一个元元素右移以后空缺的用-1来填充，因为若是第一个元素匹配失败，则需要将子串右移一位，而不需要计算子串移动的位数。
最后一个元素在右移的过程中溢出，因为原来子串中，最后一个元素的部分匹配值是其下一个元素使用的，但这个是最后一个元素，显然已没有下一个元素，故可省去。

为了下面避免由于一起讨论这两种情况会很混乱对有些人，故我把它们分开来讨论。

1、主串、子串从数组索引为 1 处开始存储字符

公式为：Move = （j - 1) - PM[ j-1 ]

next数组：

故将上式改为：

Move = （j - 1) - next[ j ]

相当于将子串的比较指针 j 回退到：

j = j - Move = j - ( (j - 1) - next[ j ] ) = next[ j ] + 1

可能有些人对上面公式表示很迷惑，接下来咱们就分析这个公式是咋推导出来的。

指针 j 回退公式的推导过程：

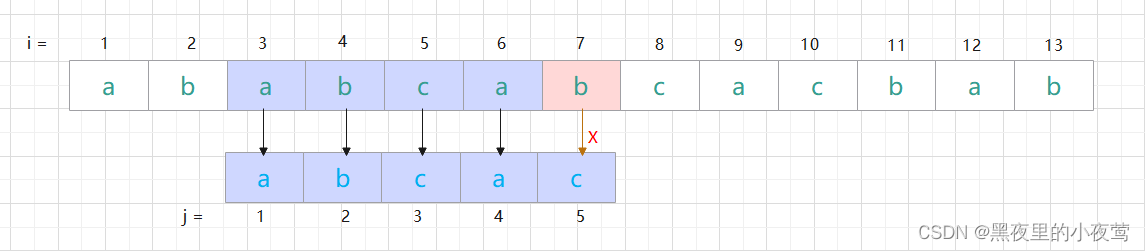
上面的 i = 7，j = 5 匹配失败，咱们之前分析得出子串应该向后移 3 位再进行下次匹配，故下次需要与 i = 7的符比较指针，咱们设其为 j' （j一撇），其需要加上 3 到匹配失败的字符处（这个例子j = 5）就可以和主串 i = 7处的字符比较，即 j' + Move = j，咱们指针回退，便是要找到这个字符在子串的位置（j'）,故 j' = j - Move = j - ( (j - 1) - next[ j ] ) = next[ j ] + 1，把 j' 改为 j 便得出上面的指针回退公式。

有时为了使公式更加简洁、计算简单，将 next 数组整体 +1（为了不进行+1的计算）

因此，上述子串的next数组也可以写成:

最终得到子串指针的变化公式 j = next[ j ]（即当匹配失败时，指针应该回退到哪）。在实际匹配过程中，子串在内存里是不会移动的，而是指针在变化，上面的画图只是为了让问题描述的更加形象。next[ j ]的含义是：在子串的第 j 个字符与主串发生失配时，则跳到子串的next[ j ]位置重新与主串的当前位置进行比较。

以上是我们分析的一些结果，那我们如何推理next数组的一般公式？设主串为 'S $_{1}$ S $_{2}$ ...S $_{n}$ '，模式串为 'P $_{1}$ P $_{2}$ ...P $_{m}$ ' ，当主串中第 i 个字符与模式串中的第 j 个字符失配时，子串应向右滑动多远，然后与模式中的哪个字符比较？

假设此时应与模式中的第 k （k < j）个字符比较，则模式中前 k-1 个字符的字符串必须满足下列条件，且不可能存在 k' > k满足下列条件：

即模式串的前j-1个字符的最长相等前后缀长度为k-1.

若存在满足上面条件的子串时，则发生失配时，仅需将模式向右滑动至模式中第 k 个字符和主串第 i 个字符对齐，此时模式中前 k - 1个字符的子串必定与主串中第 i 个字符之前长度为k-1的子串相等，由此，只需从模式第 k 个字符与主串第 i 个字符继续比较即可。如下图：

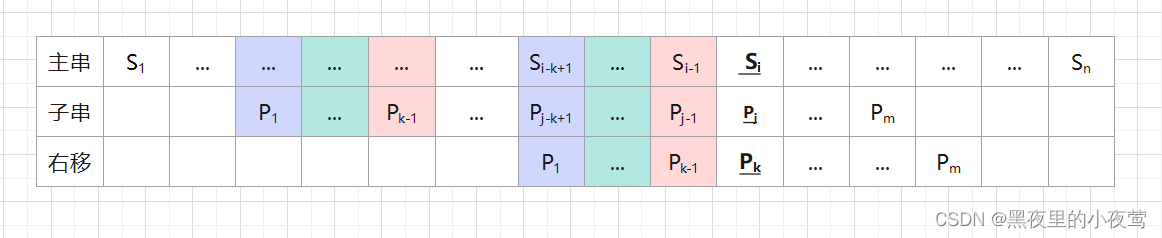
模式串右移到合适的位置（颜色相同的部分表示字符相等）

当模式串已匹配相等的序列中不存在满足上述条件的子串时（即已匹配的字符串的最长前后缀长度为 0，此时将可以看成 k = 1（对应子串的第一个字符）），显然应该将模式串右移 j - 1位，让主串第 i 个字符和模式第 1 个字符进行比较，此时右移位数最大。（和下面有所区别，它是已经匹配了一些字符，但匹配的字符串最长前后缀长度为 0，故此时主串的第 i 个字符需要重新开始和子串的第一个字符比较）

当模式串第一个字符（j = 1）与主串第 i 个字符发生失配时，规定next[ 1 ] = 0.将模式右移一位，从主串的下个位置（i + 1）和模式串的第一个字符继续比较。（和上面的有所区别，这个是刚开始匹配就失败，然后子串的第一个字符与主串的第 i + 1 个比较）

通过上面的分析可以得出next的函数公式：

上面公式不难理解，但如果想用代码来实现上面的函数貌似难度不小，接下来就进行科学的步骤：

首先由公式知

next[1] = 0

设next[ j ] = k,此时应该满足条件（已在上文提及到，再次提及下）：

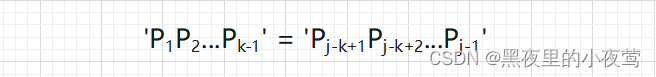
也可以用此图表示：

此时next[ j+1 ] = ？可能有两种情况：

（1）若 P $_{k}$ = P $_{j}$ ，如下图：

此时

'P $_{1}$ ...P $_{k-1}$ P $_{k}$ ' = 'P $_{j-k+1}$ ...P $_{j-1}$ P $_{j}$ '

并且不可能存在 k' > k满足上式条件，此时next[ j + 1 ] = k+1，即

next[ j+1 ] = next[ j ] + 1

这个相等也是函数get_next()（获取next数组）中的 if语句块：

if ( j == 0 || str[i] == instr[j] )
{
    ++i;
    ++j;
    next[i] = j; // 若 Pi = Pj，则 next[j+1] = next[j] + 1;
}

（2）若P $_{k}$ $\neq$ P $_{j}$ ，如下图

此时

'P $_{1}$ ...P $_{k-1}$ P $_{k}$ ' $\neq$ 'P $_{j-k+1}$ ...P $_{j-1}$ P $_{j}$ '

此时即 j 要回溯，即get_next()函数的 else语句块，也是多数人迷惑的地方，接下来我们深呼吸来战胜它吧。

else
{
    j = next[j]; // 若字符不同，则j值回溯
}

首先咱们在讨论前已知前提条件为：

'P $_{1}$ ...P $_{k-1}$ ' = 'P $_{j-k+1}$ ...P $_{j-1}$ '

也就是如下图：

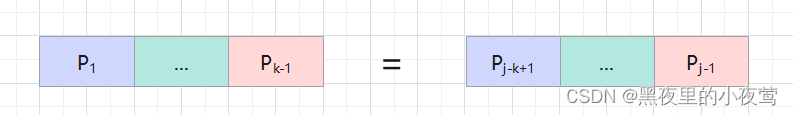
若此时'P $_{1}$ ...P $_{k-1}$ '中有最长的前后缀时（也就是next[k] = k'）,如下图：

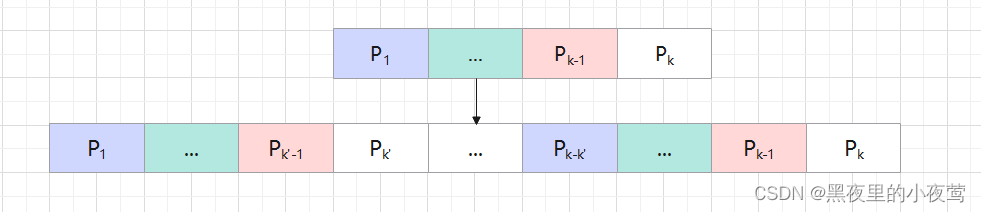
由于'P $_{1}$ ...P $_{k-1}$ ' = 'P $_{j-k+1}$ ...P $_{j-1}$ ' ，所以 'P $_{j-k+1}$ ...P $_{j-1}$ ' 分解也类似上图，咱们这下是不是将P $_{k'}$ 与P $_{j}$ 比较（即第next[k]个字符与P $_{j}$ 比较），如果此时相等（即'P $_{1}$ ...P $_{k'}$ ' = 'P $_{j-k'+1}$ ...P $_{j}$ '），则 next[j+1] = k'+1。若不相等则需要找 'P $_{1}$ ...P $_{k'}$ '的最长前后缀，将P $_{j}$ 与 P $_{k''}$ 比较，依次类推。直到找到一个k' = next[next...[k]]（1 < k' < k < j），满足下面条件：

'P $_{1}$ ...P $_{k'}$ ' = 'P $_{j-k'+1}$ ...P $_{j}$ '

得出：next[j+1] = k' + 1。

若此时'P $_{1}$ ...P $_{k-1}$ '中没有最长的前后缀时（也就是next[k] = 1），那next[ j + 1 ] = 1。

这里有个例子可以考验大家是否明白了上面的知识，Let‘s do it。

下图的模式串中求得6个字符的next值，现求next[7]，next[8]，next[9]。

答案解析：因为next[6] = 3（k = 3，但其前面的字符串'P $_{1}$ P $_{2}$ ' 的最长前后缀长度为0，最终结果应为next[7]=1）,又P $_{6}$ $\neq$ P $_{3}$ ,则需要比较P $_{6}$ 和P $_{1}$ （因next[3] = 1），由于 P $_{6}$ $\neq$ P $_{1}$ ，而next[1] = 0，所以next[7] = 1；

因为P $_{7}$ = P $_{1}$ ，则next[8] = next[7] + 1 = 2.（利用P $_{k}$ = P $_{j}$ ）；

因为P $_{8}$ = P $_{2}$ ，则next[9] = next[8] + 1 = 3. （利用P $_{k}$ = P $_{j}$ ）。

通过上面的分析，咱们就可以写出get_next函数和使用KMP算法的函数：

void get_next(char* instr, int next[], int instrlength)
{
	int i = 1, j = 0;
	next[i] = 0;
	while (i < instrlength)
		if (j == 0 || instr[i] == instr[j])
		{
			++i;
			++j;
			next[i] = j; //若Pi = Pj，则next[j+1] = next[j] + 1
		}
		else
			j = next[j]; //若字符不相等，则j值回溯
}

int Index_KMP(char* str, char* instr, int next[], int strlength, int instrlength)
{
	int i = 1, j = 1;
	while (i <= strlength && j <= instrlength)
	{
		if (j == 0 || str[i] == instr[j])
		{
			++i;         // 继续比较后续的字符
			++j;
		}
		else
			j = next[j]; // 模式串向后移
	}
	if (j > instrlength)
		return i - instrlength;
	else
		return 0;
}

2、主串、子串从数组索引为 0 处开始存储字符

公式为：Move = j - PM[ j-1 ]

next数组：

故将上面的公式改为：

Move = j - next[ j ]

相当于将子串的比较指针 j 回退到：

j = j - Move = j - ( j - next[ j ] ) = next[ j ]

此公式的推理过程和上面类似，这里就不再赘述。

因此，其对应的next数组并未改变，和原来的next数组一致：

以上是我们分析的一些结果，那我们如何推理next数组的一般公式？设主串为 'S $_{0}$ S $_{1}$ ...S $_{n}$ '，模式串为 'P $_{0}$ P $_{1}$ ...P $_{m}$ ' ，当主串中第 i 个字符与模式串中的第 j 个字符失配时，子串应向右滑动多远，然后与模式中的哪个字符比较？

假设此时应与模式中的第 k （k < j）个字符比较，则模式中前 k 个字符的字符串必须满足下列条件，且不可能存在 k' > k满足下列条件：

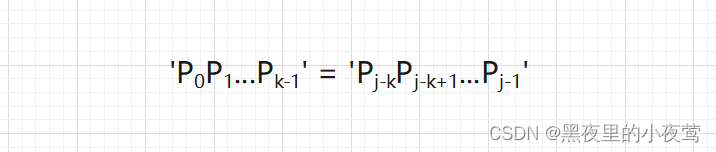
即模式串的前j-1个字符的最长相等前后缀长度为k.（数组索引是从0开始的，故索引k前有k个字符）

若存在满足上面条件的子串时，则发生失配时，仅需将模式向右滑动至模式中第 k 个字符和主串第 i 个字符对齐，此时模式中前 k 个字符的子串必定与主串中第 i 个字符之前长度为k的子串相等，由此，只需从模式第 k 个字符与主串第 i 个字符继续比较即可。如下图：

模式串右移到合适的位置（颜色相同的部分表示字符相等）

当模式串已匹配相等的序列中不存在满足上述条件的子串时（即已匹配的字符串的最长前后缀长度为 0，此时将可以看成 k = 0（对应子串的第一个字符）），显然应该将模式串右移 j 位，让主串第 i 个字符和模式第 1 个字符进行比较，此时右移位数最大。（和下面有所区别，它是已经匹配了一些字符，但匹配的字符串最长前后缀长度为 0，故此时主串的第 i 个字符需要重新开始和子串的第一个字符比较）

当模式串第一个字符（j = 0）与主串第 i 个字符发生失配时，规定next[ 1 ] = -1.将模式右移一位，从主串的下个位置（i + 1）和模式串的第一个字符继续比较。（和上面的有所区别，这个是刚开始匹配就失败，然后子串的第一个字符与主串的第 i + 1 个比较）

通过上面的分析可以得出next的函数公式：

上面公式不难理解，但如果想用代码来实现上面的函数貌似难度不小，接下来就进行科学的步骤：

首先由公式知

next[0] = -1

设next[ j ] = k,此时应该满足条件（已在上文提及到，再次提及下）：

也可以用此图表示：

此时next[ j+1 ] = ？可能有两种情况：

（1）若 P $_{k}$ = P $_{j}$ ，如下图：

此时

'P $_{0}$ ...P $_{k-1}$ P $_{k}$ ' = 'P $_{j-k}$ ...P $_{j-1}$ P $_{j}$ '

并且不可能存在 k' > k满足上式条件，此时next[ j + 1 ] = k+1，即

next[ j+1 ] = next[ j ] + 1

这个相等也是函数get_next()（获取next数组）中的 if语句块：

if ( j == -1 || str[i] == instr[j] )
{
    ++i;
    ++j;
    next[i] = j; // 若 Pi = Pj，则 next[j+1] = next[j] + 1;
}

（2）若P $_{k}$ $\neq$ P $_{j}$ ，如下图:

此时

'P $_{0}$ ...P $_{k-1}$ P $_{k}$ ' $\neq$ 'P $_{j-k}$ ...P $_{j-1}$ P $_{j}$ '

此时即 j 要回溯，即get_next()函数的 else语句块，也是多数人迷惑的地方，接下来我们深呼吸来战胜它吧。

else
{
    j = next[j]; // 若字符不同，则j值回溯
}

首先咱们在讨论前已知前提条件为：

'P $_{0}$ ...P $_{k-1}$ P $_{k}$ ' $\neq$ 'P $_{j-k}$ ...P $_{j-1}$ P $_{j}$ '

也就是如下图：

若此时'P $_{0}$ ...P $_{k-1}$ '中有最长的前后缀时（也就是next[k] = k'）,如下图：

由于 'P $_{0}$ ...P $_{k-1}$ P $_{k}$ ' = 'P $_{j-k}$ ...P $_{j-1}$ P $_{j}$ '，所以 'P $_{j-k}$ ...P $_{j-1}$ ' 分解也类似上图，咱们这下是不是将P $_{k'}$ 与P $_{j}$ 比较（即第next[k]个字符与P $_{j}$ 比较），如果此时相等（即'P $_{0}$ ...P $_{k'}$ ' = 'P $_{j-k'}$ ...P $_{j}$ '），则 next[j+1] = k'+1。若不相等则需要找 'P $_{0}$ ...P $_{k'}$ '的最长前后缀，将P $_{j}$ 与 P $_{k''}$ 比较，依次类推。直到找到一个k' = next[next...[k]]（1 < k' < k < j），满足下面条件：

'P $_{0}$ ...P $_{k'}$ ' = 'P $_{j-k'}$ ...P $_{j}$ '

得出：next[j+1] = k' + 1。

若此时'P $_{0}$ ...P $_{k-1}$ '中没有最长的前后缀时（也就是next[k] = 0），那next[ j + 1 ] = 0。

这里有个例子可以考验大家是否明白了上面的知识，Let‘s do it。

下图的模式串中求得6个字符的next值，现求next[6]，next[7]，next[8]。

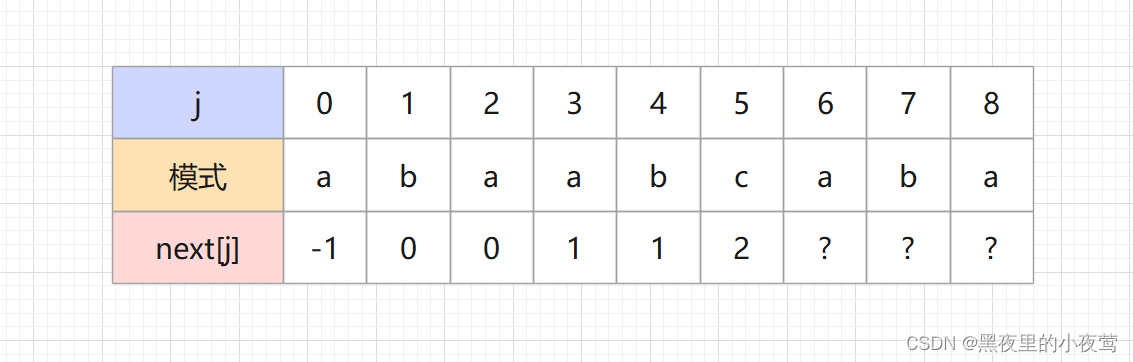
答案：next[6] = 0，next[7] = 1，next[8] = 2，其推导过程和上面的类似，（也可以直接由上面对应的结果减一便可得出相对应的结果）。

通过上面的分析，咱们就可以写出get_next函数和使用KMP算法的函数：

void get_next(char* instr, int next[], int instrlength)
{
	int i = 0, j = -1;
	next[i] = -1;
	while (i < instrlength - 1)
		if (j == -1 || instr[i] == instr[j])
		{
			++i;
			++j;
			next[i] = j; //若Pi = Pj，则next[j+1] = next[j] + 1
		}
		else
			j = next[j]; //若字符不相等，则j值回溯
}

int Index_KMP(char* str, char* instr, int next[], int strlength, int instrlength)
{
	int i = 0, j = 0;
	while (i < strlength && j < instrlength)
	{
		if (j == -1 || str[i] == instr[j])
		{
			++i;         // 继续比较后续的字符
			++j;
		}
		else
			j = next[j]; // 模式串向后移
	}
	if (j >= instrlength)
		return i - instrlength;
	else
		return 0;
}

3、例题

（1）串'ababaaababaa' 的next数组为（）

A. -1,0,1,2,3,4,5,6,7,8,8,8 B. -1,0,1,0,1,0,0,0,0,1,0,1

C. -1,0,0,1,2,3,1,1,2,3,4,5 D. -1,0,1,2,-1,0,1,2,1,1,2,3

（2）串'ababaaababaa' 的next数组为（）

A. 01234567899 B. 012121111212

C. 01123422345 D. 012301232234

答案：（1）C （2）C

注：在实际KMP算法中，为了使公式更简洁、计算简单，如果串的位序是从1开始的，则next数组才需要整体加1；如果串的位序是从0开始的，则next数组不需要整体加1。

3、KMP模式匹配算法的改进

上面的KMP算法看似好像很完善，但随着时间过去，有人发现KMP算法还是有缺陷的。比如模式串 'aaaab' 在和主串 'aaabaaaab' 进行匹配时：（这也对应上面的两种KMP算法的写法）

（1）主串、子串从数组索引为 1 处开始存储字符

当 i = 4、j = 4时，S $_{4}$ 跟P $_{4}$ （b $\neq$ a）失配，如果用之前的next数组还需要进行 S $_{4}$ 与 P $_{3}$ 、S $_{4}$ 与P $_{2}$ 、S $_{4}$ 与P $_{1}$ 这三次比较。实际上，因为P $_{next[4]=3}$ $=$ P $_{4}$ = a、P $_{next[3]=2}$ $=$ P $_{3}$ = a、P $_{next[2]=1}$ $=$ P $_{2}$ = a，显然后面3次用一个和P $_{4}$ 相同的字符更S $_{4}$ 比较毫无意义，必然失配。那么问题在哪？

问题在于不应该出现 P $_{j}$ = P $_{next[j]}$ 。理由是：当P $_{j}$ $\neq$ S $_{j}$ 时，下次匹配的必然是P $_{next[j]}$ 与 S $_{j}$ 比较，如果P $_{j}$ = P $_{next[j]}$ ，那么相当于拿一个和P $_{j}$ 相等的字符跟S $_{j}$ 比较，这必然导致继续失配，这样的比较无意义。如下图：

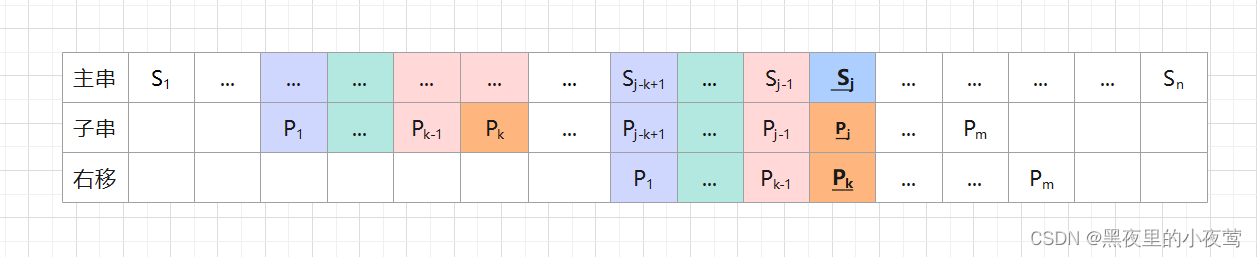
如果出现了，需要再次递归，将next[j]修改为next[next[j]]，直至两者不同为止，更新后的数组命名为nextval。

改进过的KMP算法如下：

void get_next(char* instr, int nextval[], int instrlength)
{
	int i = 1, j = 0;
	next[i] = 0;
	while (i < instrlength)
		if (j == 0 || instr[i] == instr[j])
		{
			++i;
			++j;
            if ( instr[i] != instr[j]) // 不相等，直接和原来求next数组一样
                nextval[i] = j;
            else
                nextval[i] = nextval[j]; // 相等进行递归
		}
		else
			j = next[j]; //若字符不相等，则j值回溯
}

在此解释下下面这条语句：

if ( instr[i] != instr[j])
    nextval[i] = j;
else
    nextval[i] = nextval[j];

此时 P $_{j}$ = P $_{k}$ ，如下图

然后两者自增，k = k+1, j = j+1，故需要比较这两处的字符是否相等（当P $_{j+1}$ 与主串比较失败就会跳到P $_{k+1}$ ），如果相等就要进行递归，与上面类似再次比较，直到不同。如下图：

比较：（相等递归）

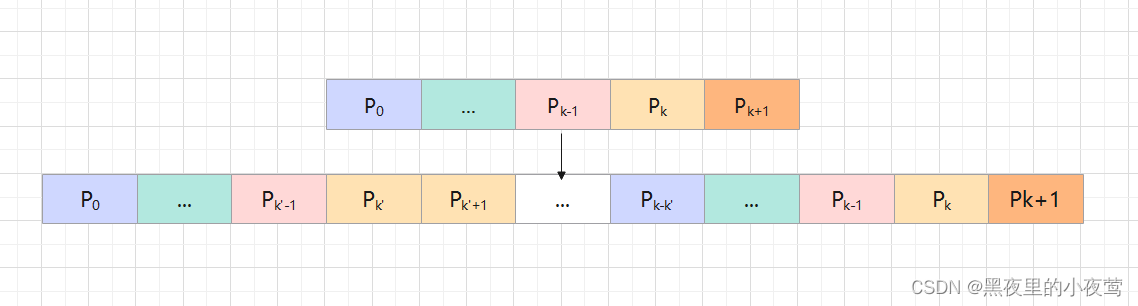此时nextval[ j ] = nextval[k+1]，但P $_{k+1}$ $\neq$ P $_{k'+1}$ （由之前的比较得出），故nextval[k+1] = k' + 1,即nextval[ j ] = k'+1。

不相等直接 P $_{j+1}$ = k + 1.

（2）主串、子串从数组索引为 0 处开始存储字符

其推理过程和上面类似，这里就不再赘述。给出改进过后的KMP算法。

void get_next(char* instr, int nextval[], int instrlength)
{
	int i = 0, j = -1;
	next[i] = -1;
	while (i < instrlength - 1)
		if (j == -1 || instr[i] == instr[j])
		{
			++i;
			++j;
			if (instr[i] != instr[j]) // 不相等，直接和原来求next数组一样
                nextval[i] = j;
            else
                nextval[i] = nextval[j]; // 相等进行递归
		}
		else
			j = next[j]; //若字符不相等，则j值回溯
}

（3）例题

(1）串'ababaaababaa' 的nextval数组为（）

A. 0,1,0,1,1,2,0,1,0,1,0,2 B. 0,1,0,1,1,4,1,1,0,1,0,2

C. 0,1,0,1,0,4,2,1,0,1,0,4 D. 0,1,1,1,0,2,1,1,0,1,0,4

答案：（1）C

解析：

注：一般求串的nextval数组，先求出其next数组，再根据next数组求出nextval数组。

四、测试程序

（1）朴素的模式匹配算法（第一种写法）

#include <stdio.h>
#include <string.h>

#define MAXSIZE 100

int Index(char* str, char* instr, int strlength, int instrlength);

int main(void)
{
	int strlength, instrlength;
	char str[MAXSIZE];
	char instr[50];
	printf("欢迎使用简单的模式匹配算法测试程序！！！\n");
	printf("你需要输入主串和模式串，此程序会返回模式串在主串的位置\n");
	printf("获取主串：");
	scanf("%s", str);
	printf("获取模式串：");
	scanf("%s", instr);
	strlength = strlen(str);
	instrlength = strlen(instr);
	int index = Index(str, instr, strlength, instrlength) + 1;
	printf("模式串在主串的位置：%d", index);
	return 0;
}

int Index(char* str, char* instr, int strlength, int instrlength)
{
	int i = 0, j = 0;
	while (i < strlength && j < instrlength)
	{
		if (str[i] == instr[j])
		{
			++i;   // 比较后续的字符
			++j;
		}
		else
		{
			i = i - j + 1; // 指针后退重新开始匹配
			j = 0;
		}
	}
	if (j >= instrlength)
		return i - instrlength;
	else
		return 0;
}

（2）KMP模式匹配算法（第二种：主串、子串从数组索引0处开始）

#include <stdio.h>
#include <string.h>  // 提供strlen()函数，返回字符串多长
#include <stdlib.h> // 提供malloc()函数

#define MAXSIZE 100

void get_next(char* instr, int next[], int instrlength);
int Index_KMP(char* str, char* instr, int next[], int strlength, int instrlength);

int main(void)
{
	char str[MAXSIZE];
	char instr[50];
	int strlength, instrlength;
	printf("欢迎使用KMP算法测试程序！！！\n");
	printf("你需要输入主串和子串，此程序会返回子串在主串的位置\n");
	printf("获取主串：");
	scanf("%s", str);
	printf("获取子串：");
	scanf("%s", instr);
	instrlength = strlen(instr);
	strlength = strlen(str);
	int* next = (int*)malloc(sizeof(int) * instrlength);
	get_next(instr, next, instrlength);
	int index = Index_KMP(str, instr, next, strlength, instrlength) + 1;
	printf("子串在主串的位置为：%d\n", index);
	return 0;
}

void get_next(char* instr, int next[], int instrlength)
{
	int i = 0, j = -1;
	next[i] = -1;
	while (i < instrlength - 1)
		if (j == -1 || instr[i] == instr[j])
		{
			++i;
			++j;
			next[i] = j;
		}
		else
			j = next[j];
}

int Index_KMP(char* str, char* instr, int next[], int strlength, int instrlength)
{
	int i = 0, j = 0;
	while (i < strlength && j < instrlength)
	{
		if (j == -1 || str[i] == instr[j])
		{
			++i;         // 继续比较后续的字符
			++j;
		}
		else
			j = next[j]; // 模式串向后移
	}
	if (j >= instrlength)
		return i - instrlength;
	else
		return 0;
}