二叉树查找结点及父结点

编写程序在二叉树中查找给定结点及父结点。二叉树结点的数据域值不等于0的整数。

输入格式:

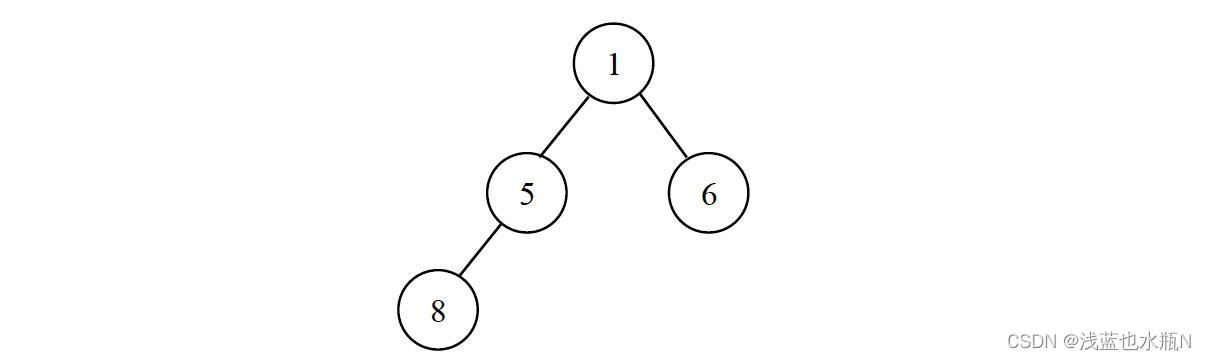
输入第1行为一组用空格间隔的整数，表示带空指针信息的二叉树先根序列，其中空指针用0表示。例如1 5 8 0 0 0 6 0 0表示如下图的二叉树。第2行为整数m，表示查询个数。接下来m行，每行为一个不等于0的整数K，表示要查找的结点的数据值。m不超过100，二叉树结点个数不超过150000，高度不超过6000。输入数据保证二叉树各结点数据值互不相等。

输出格式:

输出为m行，每行1个整数，表示被查找结点K的父结点数据值，若二叉树中无结点K或结点K无父结点，则输出0。

输入样例:

1 5 8 0 0 0 6 0 0
3
8
1
6

输出样例:

5
0
1

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
typedef struct BiTNode {
	int data;
	struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;

BiTree CreateBiTree(BiTree T);
int PreTraverse(int x, BiTree T, BiTree F);
int main() {
	int n, i, x, y;
	BiTree T = NULL;
	T = CreateBiTree(T);
	scanf("%d", &n);
	for (i = 0; i < n; ++i)
	{
		scanf("%d", &x);
		y = PreTraverse(x, T, T);
		if ((y==T->data&&x==y)||!y)//排除根节点
		{
			printf("0\n");
		}
		else
			printf("%d\n",y);

	}
	return 0;
}
BiTree CreateBiTree(BiTree T)
{
	int ex;
	scanf("%d", &ex);
	if (ex == 0)
		T = NULL;
	else
	{
		T = (BiTree)malloc(sizeof(BiTNode));
		T->data = ex;
		T->lchild = CreateBiTree(T->lchild);
		T->rchild = CreateBiTree(T->rchild);
	}
	return T;
}
int PreTraverse(int x, BiTree T, BiTree F)
{

	if (!T)
		return 0;
	int a, b;
	if (x == T->data)
		return F->data;
	else
	{
		F = T;//记录根节点
		a = PreTraverse(x, T->lchild, F);
		b = PreTraverse(x, T->rchild, F);
		return a ? a : b;
	}
}
/*也可以直接返回要查找的节点，他人更优代码
* BiTree PreTraverse(int x,BiTree T)
* {
	if(!T)
	return T;
	
    if((T->lchild != NULL && T->lchild->data == x) || (T->rchild != NULL && T->rchild->data == x))//要优先判断子树是否为空,不然会内存溢出
        return T;
    BiTree result = DFS(x,T->lchild);//先查左子树，再查右子树
    if(result!=NULL)
        return result;
    return DFS(x,T->rchild);
* } 
	版权声明：本文为CSDN博主「qq_59011427」的原创文章，遵循CC 4.0 BY - SA版权协议，转载请附上原文出处链接及本声明。
	原文链接：https ://blog.csdn.net/qq_59011427/article/details/127810975
*/